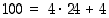 ,
kello siirtyy neljä tuntia eteenpäin.
,
kello siirtyy neljä tuntia eteenpäin.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Ajatellaanpa kysymyksiä "mitä kello on sadan tunnin kuluttua?" tai "mikä viikonpäivä on tuhannen yön jälkeen?" Miten saamme vastauksen näihin?
Edellisessä tapauksessa laskemme kuinka monta vuorokautta eli 24 tunnin jaksoa sataan tuntiin mahtuu ja katsomme, mitä jää yli. Koska 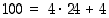 ,
kello siirtyy neljä tuntia eteenpäin.
,
kello siirtyy neljä tuntia eteenpäin.
Jälkimmäiseen kysymykseen vastaamme samaan tapaan. Koska viikossa on seitsemän päivää ja 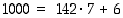 ,
on tuhannen yön jälkeen edetty kuusi viikonpäivää eteenpäin eli silloin on laskentahetkeä edeltävä viikonpäivä.
,
on tuhannen yön jälkeen edetty kuusi viikonpäivää eteenpäin eli silloin on laskentahetkeä edeltävä viikonpäivä.
Kummassakaan tapauksessa emme loppupäätelmässä tarvitse tietoa, montako vuorokautta tai viikkoa kyseiseen ajanjaksoon on mahtunut, vaan vastauksen antamiseen riittää tietää, mitä jäi yli.
Tarkastellaankin seuraavassa lähemmin kiinteälle jakajalle 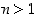 jakoyhtälössä esiintyviä jakojäännöksiä. Kun
jakoyhtälössä esiintyviä jakojäännöksiä. Kun 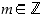 ,
jakoyhtälön mukaan on
,
jakoyhtälön mukaan on
joillekin 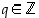 ja
ja 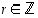 ,
missä
,
missä 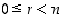 . Tällaisessa tilanteessa luvut
. Tällaisessa tilanteessa luvut 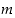 ja
ja 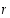 eroavat toisistaan luvun
eroavat toisistaan luvun 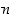 monikerralla, ts. erotus
monikerralla, ts. erotus 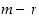 on jaollinen luvulla
on jaollinen luvulla 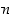 .
.
Yleisesti sanotaan, että kokonaisluvulle 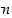 kokonaisluvut
kokonaisluvut 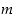 ja
ja 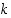 ovat (keskenään)
kongruentteja
modulo
ovat (keskenään)
kongruentteja
modulo 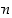 ,
jos
moduli
,
jos
moduli 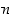 jakaa niiden erotuksen
jakaa niiden erotuksen 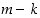 ; merkitään silloin, että
; merkitään silloin, että 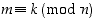 . Siis
. Siis
Tälle kongruenssikäsitteelle on varsin helppo todeta seuraavat ominaisuudet:
Relaatioita, jotka toteuttavat nämä kolme ehtoa (nimiltään refleksiivisyys, symmetrisyys ja transitiivisuus), sanotaan yleisemmin ekvivalenssirelaatioiksi. Tällaisille relaatioille on ominaista, että ne määräävät osituksen siihen joukkoon, jossa ne on määritelty. Tämä taas tarkoittaa sitä, että keskenään ekvivalentit alkiot muodostavat erillisiä osajoukkoja, joiden yhdiste on koko määrittelyjoukko.
Kongruenssit 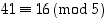 ja
ja 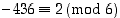 pätevät, sillä
pätevät, sillä 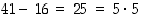 ja
ja 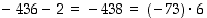 . Sen sijaan
. Sen sijaan 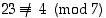 ,
sillä
,
sillä 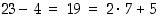 .
.
Opiskelutehtävä 23. (Kongruentit luvut)
Määrää kaikki ne kokonaisluvut 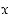 väliltä
väliltä 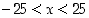 ,
jotka toteuttavat ehdon
,
jotka toteuttavat ehdon 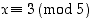 .
.
Opiskelutehtävä 24. (Lukujen kongruenttisuus)
Päättele seuraavista, päteekö se vai eikö se päde?
Opiskelutehtävä 25. (Kongruenssiyhtälöiden ratkaiseminen)
Etsi kaikki kokonaisluvut 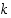 ,
jotka toteuttavat annetun ehdon:
,
jotka toteuttavat annetun ehdon:
Kun kokonaisluvulle 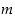 on jakoyhtälön mukaisesti
on jakoyhtälön mukaisesti 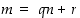 ,
luku
,
luku 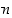 jakaa erotuksen
jakaa erotuksen 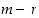 ,
ts.
,
ts. 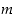 on kongruentti (modulo
on kongruentti (modulo 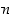 ) luvun
) luvun 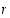 kanssa. Jokainen kokonaisluku
kanssa. Jokainen kokonaisluku 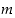 on siten kongruentti (modulo
on siten kongruentti (modulo 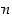 ) jonkin luvun
) jonkin luvun 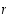 ,
,
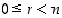 ,
kanssa.
,
kanssa.
Keskenään kongruenteista luvuista saadaan aikaan seuraavat joukot, ns.
jäännösluokat (modulo 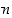 ):
):
Muita jäännösluokkia ei olekaan, sillä
Huomaa, että erikoisesti 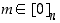 täsmälleen silloin, kun
täsmälleen silloin, kun 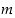 on jaollinen luvulla
on jaollinen luvulla 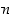 .
.
Merkitään näiden joukkojen muodostamaa joukkoa symbolilla 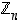 ,
siis
,
siis
Nämä osajoukot muodostavat siis erään kokonaislukujen 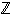 osituksen, eli sen jaon erillisiin osajoukkoihin. Joukkoa
osituksen, eli sen jaon erillisiin osajoukkoihin. Joukkoa 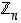 tullaan sanomaan
jäännösluokkarenkaaksi (ks. lauseen 3.2.3 jälkeinen selitys).
tullaan sanomaan
jäännösluokkarenkaaksi (ks. lauseen 3.2.3 jälkeinen selitys).
Kun 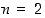 ,
joukko
,
joukko 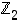 koostuu kahdesta alkiosta (joukosta)
koostuu kahdesta alkiosta (joukosta)
Tapauksessa 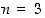 joukko
joukko 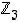 koostuu kolmesta alkiosta
koostuu kolmesta alkiosta
Joukossa 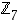 on
on 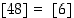 ,
koska
,
koska 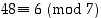 ,
mikä taas pätee, koska
,
mikä taas pätee, koska 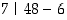 .
.
Tehtävä. Etsi pienin ei-negatiivinen luku jäännösluokasta 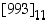 .
.
Tehtävä. Kuinka monta alkiota on joukossa 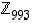 ?
?
1. Määrää kullekin annetulle luvulle ja modulille pienin positiivinen kokonaisluku, jonka kanssa annettu luku on kongruentti:
a) 999 (mod 50), b) −999 (mod 25), c) 999 (mod 37).
2. Tarkastele lukuja 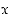 ,
joille
,
joille 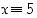 (mod 13). Määrää itseisarvoltaan pienin luku
(mod 13). Määrää itseisarvoltaan pienin luku 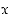 ,
jolle a)
,
jolle a) 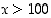 ,
b)
,
b) 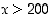 ja c)
ja c) 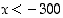 .
.