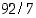 muodossa
muodossa
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Esittäessämme murtoluvun 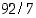 muodossa
muodossa
käytämme itse asiassa hyväksi yhtälöä 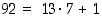 . Yleisemmin, kun kaksi luonnollista lukua jaetaan tällä tavalla, saadaan ilmeisesti aina aikaan jakotuloksen kokonaisosa ja jakojäännös. Tämä ns. jakoyhtälö osoitetaan seuraavassa oikeaksi pienimmän alkion periaatteella.
. Yleisemmin, kun kaksi luonnollista lukua jaetaan tällä tavalla, saadaan ilmeisesti aina aikaan jakotuloksen kokonaisosa ja jakojäännös. Tämä ns. jakoyhtälö osoitetaan seuraavassa oikeaksi pienimmän alkion periaatteella.
Koska samat tarkastelut voidaan tehdä jatkossa usein myös negatiivisille luvuille, siirrymme tarkastelemaan kaikkien kokonaislukujen joukkoa
Tässä esiintyvät negatiiviset luvut voidaan matemaattisesti määritellä luonnollisten lukujen 'väärässä järjestyksessä' tehdyillä erotuksilla:
Todistamme tulevien tarkastelujen perustaksi heti kokonaislukuja koskevan jakoyhtälön.
Kahdelle kokonaisluvulle 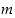 ja
ja 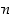 ,
joista
,
joista 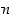 on positiivinen, on olemassa yksikäsitteisesti määrätyt kokonaisluvut
on positiivinen, on olemassa yksikäsitteisesti määrätyt kokonaisluvut 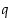 ja
ja 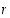 siten, että
siten, että
Tässä yhtälössä 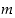 on
jaettava,
on
jaettava,
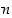 on
jakaja,
on
jakaja,
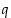 on
jakotulos (tai osamäärä) ja
on
jakotulos (tai osamäärä) ja 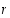 on
jakojäännös (eli "jaettava = jakotulos . jakaja + jakojäännös").
on
jakojäännös (eli "jaettava = jakotulos . jakaja + jakojäännös").
Todistus. Havainnollistetaan väitettä ensin reaaliakselilla alla olevilla kuvioilla.
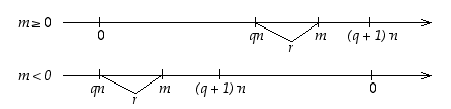
Jakoyhtälön olemassaolon todistamiseksi tarkastellaan luonnollisten lukujen osajoukkoa
Se ei ole tyhjä joukko, sillä ainakin 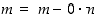 on sen alkio. Pienimmän alkion periaatteen mukaan joukossa
on sen alkio. Pienimmän alkion periaatteen mukaan joukossa 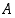 on pienin alkio, olkoon se
on pienin alkio, olkoon se 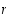 . Joukon
. Joukon 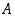 alkiona sillä on esitys
alkiona sillä on esitys 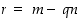 jollekin kokonaisluvulle
jollekin kokonaisluvulle 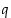 . Siten
. Siten 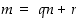 . Lisäksi tässä
. Lisäksi tässä 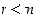 ,
sillä jos olisi päinvastoin
,
sillä jos olisi päinvastoin 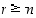 ,
olisi luku
,
olisi luku 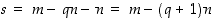 lukua
lukua 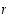 pienempi joukon
pienempi joukon 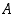 alkio.
alkio.
Osoitamme sitten jakoyhtälön yksikäsitteisyyden. Oletetaan, että on kaksi esitystä
Koska silloin 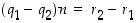 ,
riittää osoittaa, että
,
riittää osoittaa, että 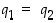 . Jos olisi
. Jos olisi 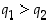 ,
olisi
,
olisi 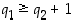 ja edelleen
ja edelleen 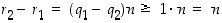 ,
mikä on mahdotonta. Samasta syystä vaihtoehto
,
mikä on mahdotonta. Samasta syystä vaihtoehto 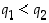 ei käy. Siten on oltava
ei käy. Siten on oltava 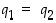 . Silloin myös
. Silloin myös 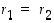 .
.
Luvuille 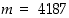 ja
ja 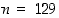 saadaan laskimella jakotulokseksi likiarvo 32,46. Kun valitaan tämän kokonaisosa 32 jakotulokseksi
saadaan laskimella jakotulokseksi likiarvo 32,46. Kun valitaan tämän kokonaisosa 32 jakotulokseksi 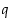 ,
saadaan jakojäännökseksi
,
saadaan jakojäännökseksi 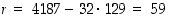 . Annetuille luvuille
. Annetuille luvuille 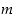 ja
ja 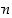 jakoyhtälö on siten muotoa
jakoyhtälö on siten muotoa 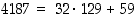 ,
ts. niille
,
ts. niille 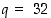 ja
ja 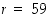 .
.
Jakoyhtälön erikoistapaus saadaan silloin, jos jakojäännös sattuu olemaan nolla, ts. jos jako sattuu menemään tasan. Jos kokonaisluvuille 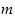 ja
ja 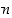 on
on 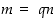 jollekin kokonaisluvulle
jollekin kokonaisluvulle 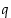 ,
sanotaan, että luku
,
sanotaan, että luku 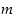 on
jaollinen luvulla
on
jaollinen luvulla 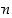 ,
tai että
,
tai että 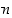 on luvun
on luvun 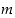 tekijä,
tai että
tekijä,
tai että 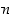 jakaa luvun
jakaa luvun 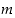 ,
merkitään
,
merkitään 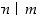 (jolloin pystyviivan voi lukea jakaa-sanana). Siis
(jolloin pystyviivan voi lukea jakaa-sanana). Siis
Tehtävä. Määrää kaikki luvun 45 tekijät. Määrää edelleen luvun 60 kaikki positiiviset tekijät.
Opiskelutehtävä 13. (Kokonaisluvun positiiviset tekijät)
Määrää kaikki luvun 496 positiiviset tekijät ja laske ne yhteen. Mitä huomaat? Eräällä luvulla lukujen 20 ja 30 välissä on sama ominaisuus. Millä?
Seuraavassa on tärkeimpiä jaollisuuden perusominaisuuksia.
(b) Jos 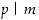 ja
ja 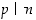 ,
niin
,
niin 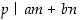 kaikilla kokonaisluvuilla
kaikilla kokonaisluvuilla 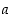 ja
ja 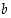 .
.
Todistus. (a) Oletuksen mukaan 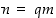 ja
ja 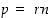 joillekin kokonaisluvuille
joillekin kokonaisluvuille 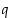 ja
ja 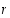 ,
joten
,
joten 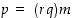 eli
eli 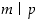 .
.
(b) Tämän kohdan oletuksen mukaan 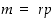 ja
ja 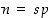 ,
joten kaikilla kokonaisluvuilla
,
joten kaikilla kokonaisluvuilla 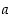 ja
ja 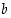 on
on
(c) Jos luku 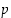 jakaisi summan
jakaisi summan 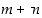 ,
oletuksen
,
oletuksen 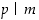 ja kohdan (b) mukaan se jakaisi myös luvun
ja kohdan (b) mukaan se jakaisi myös luvun 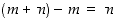 ,
mikä on vastoin oletusta. Siis
,
mikä on vastoin oletusta. Siis 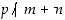 .
.
(d) Koska oletuksen mukaan 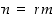 ja
ja 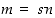 ,
on
,
on 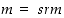 . Jos
. Jos 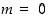 ,
myös
,
myös 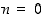 . Jos taas
. Jos taas 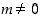 ,
yhtälöstä
,
yhtälöstä 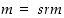 seuraa, että
seuraa, että 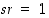 ja siten joko
ja siten joko 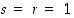 tai
tai 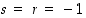 . Joka tapauksessa pätee, että
. Joka tapauksessa pätee, että 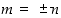 .
.
Opiskelutehtävä 14. (Jaollisuuden todistaminen induktiolla)
Osoita (induktiolla), että luonnollisille luvuille 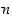 pätee: a)
pätee: a) 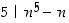 ja b)
ja b) 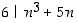 .
.
Kahdella eri luvulla voi olla samoja lukuja tekijöinään. Ne ovat näiden lukujen yhteisiä tekijöitä.
Tehtävä. Määrää lukujen 45 ja 60 kaikki yhteiset tekijät.
Määrittelemme edelleen, että nollasta eroavien kokonaislukujen 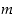 ja
ja 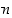 suurin yhteinen tekijä
suurin yhteinen tekijä  on näiden yhteinen positiivinen tekijä, joka on jaollinen kaikilla muilla yhteisillä tekijöillä. Toisin sanoen luonnollinen luku
on näiden yhteinen positiivinen tekijä, joka on jaollinen kaikilla muilla yhteisillä tekijöillä. Toisin sanoen luonnollinen luku 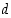 on
on 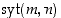 ,
jos se toteuttaa seuraavat kaksi ehtoa:
,
jos se toteuttaa seuraavat kaksi ehtoa:
Lisäksi sovitaan, että 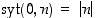 ,
kun
,
kun 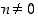 .
.
Tehtävä. Mikä lukujen 45 ja 60 yhteisistä tekijästä on suurin? Mitä voit jaollisuuden mielessä sanoa muitten suhteesta suurimpaan (muuta kuin, että ne ovat pienempiä)? Onko tämä yhteisten tekijöiden suurin luku myös suurin yhteinen tekijä edellä olevan määrittelyn mukaan?
On selvää, etteivät lukujen merkit vaikuta suurimpaan yhteiseen tekijään, joten
Voimme siis tarkasteluissa yleisesti ilman rajoituksia olettaa, että kaikki tarkasteltavat luvut ovat positiivisia. Selvää on myös, että luvun ja sen tekijän suurin yhteinen tekijä on se tekijä:
Isoille luvuille yhteisten tekijöiden etsiminen on työläs tehtävä. On osoitettu jopa, että ei ole olemassa mitään nopeaa ja yleisesti toimivaa algoritmia, joilla kokonaislukujen tekijät voitaisiin määrätä. Täysin yllättävää onkin, että paitsi etsimällä yhteisten tekijöiden joukosta suurinta, suurin yhteinen tekijä voidaan määrätä suoraankin, ilman muiden tekijöiden etsimistä. Tämän jo Eukleideen tunteman menettelyn johtamiseksi todetaan ensin, että suurinta yhteistä tekijää määrättäessä toista lukua voidaan muuttaa toisen monikerralla.
Nollasta eroaville kokonaisluvulle 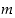 ja
ja 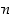 on
on
Jokainen lukujen 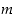 ja
ja 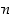 yhteinen tekijä on myös luvun
yhteinen tekijä on myös luvun 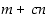 tekijä. Ja päinvastoin lukujen
tekijä. Ja päinvastoin lukujen 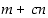 ja
ja 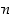 yhteinen tekijä on myös luvun
yhteinen tekijä on myös luvun 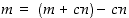 tekijä. Tarkasteltavilla lukupareilla on siis samat yhteinen tekijät ja siten myös sama suurin yhteinen tekijä.
tekijä. Tarkasteltavilla lukupareilla on siis samat yhteinen tekijät ja siten myös sama suurin yhteinen tekijä.
Kahden luvun suurinta yhteistä tekijää määrättäessä voimme siis suuremmasta luvusta vähentää pienemmän monikertoja ilman että suurin yhteinen tekijä muuttuu. Esimerkiksi luvuille 4187 ja 129 on jakoyhtälön mukaan 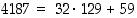 ,
joten
,
joten
Käyttämällä saatuun lukupariin uudelleen jakoyhtälöä voimme edelleen pienentää suurempaa lukua: koska 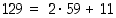 ,
on
,
on
Tällä parilla ei selvästikään ole ykköstä isompia tekijöitä, joten niitä ei ole alkuperäisellä lukuparillakaan. Tällaisen päättelyn toistamiseen perustuukin ns. Eukleideen algoritmi suurimman yhteisen tekijän määräämiseksi. Esitetään seuraavassa sen yleiset vaiheet ja palataan sen jälkeen vielä äskeiseen esimerkkiin.
Lause 2.2.5. (Eukleideen algoritmi)
Olkoot 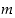 ja
ja 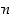 positiivisia kokonaislukuja. Näiden suurin yhteinen tekijä
positiivisia kokonaislukuja. Näiden suurin yhteinen tekijä 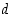 saadaan seuraavalla algoritmilla:
saadaan seuraavalla algoritmilla:
1° Jaetaan luku 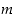 luvulla
luvulla 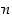 jakoyhtälön mukaisesti:
jakoyhtälön mukaisesti:
Jos tässä 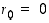 ,
valitaan
,
valitaan 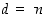 ja lopetetaan.
ja lopetetaan.
2° Jos 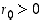 ,
muodostetaan jakoyhtälö luvuille
,
muodostetaan jakoyhtälö luvuille 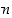 ja
ja 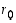 :
:
Jos tässä 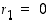 ,
valitaan
,
valitaan 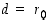 ja lopetetaan.
ja lopetetaan.
3° Tästä eteenpäin jatketaan seuraavan periaatteen mukaisesti: Aina, jos jakojäännös on nolla, valitaan edellinen jakojäännös luvuksi 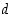 . Jos taas jakojäännös ei ole nolla, muodostetaan uusi jakoyhtälö niin, että edellinen jakaja siirretään uudeksi jaettavaksi ja edellinen jakojäännös uudeksi jakajaksi.
. Jos taas jakojäännös ei ole nolla, muodostetaan uusi jakoyhtälö niin, että edellinen jakaja siirretään uudeksi jaettavaksi ja edellinen jakojäännös uudeksi jakajaksi.

4° Koska tällaisessa menettelyssä uusi jakojäännös on aina edellistä pienempi, ei pienimmän alkion (tai rajallisen laskeutumisen) periaatteen johdosta jakojäännös voi olla loputtomasti positiivinen, vaan jossain vaiheessa jakojäännökseksi on tultava nolla. Silloin, olkoon se vaiheessa 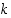 ,
saadaan seuraavanlainen tilanne:
,
saadaan seuraavanlainen tilanne:
5° Valitaan 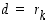 ,
ts. valitaan viimeinen nollasta eroava jakojäännös suurimmaksi yhteiseksi tekijäksi.
,
ts. valitaan viimeinen nollasta eroava jakojäännös suurimmaksi yhteiseksi tekijäksi.
Todistus. Perustellaan lyhyesti algoritmin toimivuus. Ensinnäkin, viimeisestä yhtälöstä nähdään, että 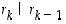 . Tällöin myös
. Tällöin myös 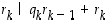 eli
eli 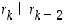 . Näin päättelyä jatkamalla (ja tarvittaessa induktiolla todistamalla) nähdään, että luku
. Näin päättelyä jatkamalla (ja tarvittaessa induktiolla todistamalla) nähdään, että luku 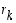 jakaa jokaisen edeltävistä jakojäännöksistä ja lopulta myös luvut
jakaa jokaisen edeltävistä jakojäännöksistä ja lopulta myös luvut 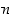 ja
ja 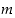 . Luku
. Luku 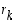 on siis näiden yhteinen tekijä.
on siis näiden yhteinen tekijä.
(joillekin kokonaisluvuille 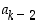 ja
ja 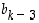 ), voidaan ilmeisesti (ja täydellisellä induktiolla todistaen)
), voidaan ilmeisesti (ja täydellisellä induktiolla todistaen) 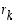 ilmoittaa muodossa
ilmoittaa muodossa
Tämän yhtälön ja lauseen 2.2.3 kohdan (b) perusteella jokainen lukujen 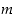 ja
ja 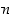 yhteinen tekijä on myös luvun
yhteinen tekijä on myös luvun 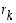 tekijä.
tekijä.
Määritelmän mukaan luku 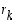 on lukujen
on lukujen 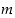 ja
ja 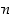 suurin yhteinen tekijä.
suurin yhteinen tekijä.
Tehtävä. Määrää Eukleideen algoritmilla lukujen 345 ja 45 suurin yhteinen tekijä.
Nollasta eroavien kokonaislukujen 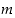 ja
ja 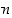 suurin yhteinen tekijä
suurin yhteinen tekijä 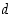 voidaan esittää muodossa
voidaan esittää muodossa
Todistus. Katso Eukleideen algoritmin 2.2.5 todistuksen loppuosa.
Muotoa 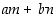 ,
missä
,
missä 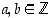 ,
olevaa summaa sanomme lukujen
,
olevaa summaa sanomme lukujen 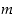 ja
ja 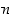 monikertasummaksi. Myös lineaarialgebrallista termiä "kokonaislukukertoiminen lineaarikombinaatio" käytetään yleisesti.
monikertasummaksi. Myös lineaarialgebrallista termiä "kokonaislukukertoiminen lineaarikombinaatio" käytetään yleisesti.
Opiskelutehtävä 15. (Kahden luvun yhteiset tekijät)
Ilmoita luvuille 60 ja 84 a) niiden positiiviset tekijät, b) niiden yhteiset positiiviset tekijät, c) niiden suurin yhteinen tekijä, ja d) yritä keksiä tälle jokin esitys alkuperäisten lukujen monikertasummana.
Edellisessä esimerkissä 2.2.6 saatiin lukujen 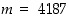 ja
ja 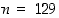 suurimmaksi yhteiseksi tekijäksi
suurimmaksi yhteiseksi tekijäksi 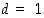 . Esitetään se muodossa
. Esitetään se muodossa 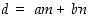 :
:
Luvuiksi 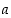 ja
ja 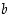 kelpaavat siis esimerkiksi luvut
kelpaavat siis esimerkiksi luvut 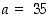 ja
ja 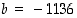 .
.
Huomaa, että monikertasumman kertoimia 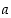 ja
ja 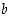 ratkaistaessa, ns. 'paluualgoritmia' tehtäessä, laskuissa esiintyviä jakojäännöksiä ei kerrota koskaan, vaan vain näiden kertoimia yhdistellään. Se jakojäännös, joka on luvun
ratkaistaessa, ns. 'paluualgoritmia' tehtäessä, laskuissa esiintyviä jakojäännöksiä ei kerrota koskaan, vaan vain näiden kertoimia yhdistellään. Se jakojäännös, joka on luvun 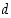 ratkaisualgoritmissa, 'menoalgoritmissa', myöhemmin saatu, korvataan aina kahden edellisen jakojäännöksen monikertasummalla, kunnes lopulta saadaan lukujen
ratkaisualgoritmissa, 'menoalgoritmissa', myöhemmin saatu, korvataan aina kahden edellisen jakojäännöksen monikertasummalla, kunnes lopulta saadaan lukujen 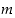 ja
ja 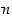 monikertasumma.
monikertasumma.
Opiskelutehtävä 16. (Suurin yhteinen tekijä Euklideen algoritmilla)
Määrää Eukleideen algoritmilla lukujen 60 ja 84 suurin yhteinen tekijä ja sille esitys näiden lukujen monikertasummana.
Suurimman yhteisen tekijän esityksessä 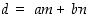 kertoimet
kertoimet 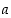 ja
ja 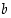 eivät ole yksikäsitteiset, koska näiden tilalle voi aina sijoittaa myös luvut
eivät ole yksikäsitteiset, koska näiden tilalle voi aina sijoittaa myös luvut 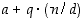 ja
ja 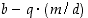 ,
missä
,
missä 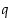 voi olla mikä tahansa kokonaisluku. Jos toisaalta jokin muu luku
voi olla mikä tahansa kokonaisluku. Jos toisaalta jokin muu luku 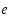 voidaan esittää muodossa
voidaan esittää muodossa 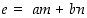 ,
silloin lukujen
,
silloin lukujen 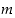 ja
ja 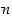 suurin yhteinen tekijä
suurin yhteinen tekijä 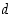 jakaa luvun
jakaa luvun 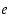 . Olemme siten todenneet oikeaksi seuraavan karakterisoinnin.
. Olemme siten todenneet oikeaksi seuraavan karakterisoinnin.
Nollasta eroavien kokonaislukujen 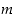 ja
ja 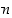 suurin yhteinen tekijä
suurin yhteinen tekijä 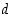 on pienin positiivinen luku
on pienin positiivinen luku 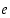 ,
joka voidaan esittää muodossa
,
joka voidaan esittää muodossa 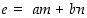 ,
missä
,
missä 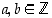 .
.
Jos erikoisesti 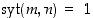 ,
kuten esimerkissä 2.2.6, sanomme, että luvut
,
kuten esimerkissä 2.2.6, sanomme, että luvut 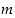 ja
ja 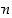 ovat
keskenään jaottomat tai
suhteellisesti jaottomat. Puhutaan myös
suhteellisista
alkuluvuista. Nämä ovat vakiintuneita termejä, kuvaavampia voisivat olla 'yhteistekijättömät' tai 'keskenään supistumattomat'. Huomaa, että keskenään jaottomuus ei tarkoita sitä, että luvut eivät jaa toisiaan, vaan sitä, että niillä ei ole ykköstä isompia yhteisiä tekijöitä.
ovat
keskenään jaottomat tai
suhteellisesti jaottomat. Puhutaan myös
suhteellisista
alkuluvuista. Nämä ovat vakiintuneita termejä, kuvaavampia voisivat olla 'yhteistekijättömät' tai 'keskenään supistumattomat'. Huomaa, että keskenään jaottomuus ei tarkoita sitä, että luvut eivät jaa toisiaan, vaan sitä, että niillä ei ole ykköstä isompia yhteisiä tekijöitä.
Tehtävä. Ovatko luvut 15 ja 28 keskenään jaottomat? Entä 35 ja 84?
Nollasta eroavat kokonaisluvut 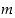 ja
ja 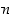 ovat keskenään jaottomat täsmälleen silloin, kun
ovat keskenään jaottomat täsmälleen silloin, kun 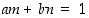 joillekin
joillekin 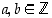 .
.
Todistus. Kokonaisluvut 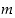 ja
ja 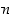 ovat keskenään jaottomat, jos ja vain jos niiden suurin yhteinen tekijä on yksi. Lauseiden 2.2.7 ja 2.2.9 perusteella tämä on taas yhtäpitävää sen kanssa, että
ovat keskenään jaottomat, jos ja vain jos niiden suurin yhteinen tekijä on yksi. Lauseiden 2.2.7 ja 2.2.9 perusteella tämä on taas yhtäpitävää sen kanssa, että 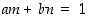 joillekin kokonaisluvuille
joillekin kokonaisluvuille 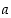 ja
ja 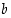 .
.
Seuraavassa on eräitä tavallisimpia suurimman yhteisen tekijän ominaisuuksia. Näiden todistukset sivuutetaan tässä.
Olkoot 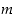 ,
,
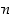 ja
ja 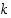 nollasta eroavia kokonaislukuja. Tällöin seuraavat pätevät:
nollasta eroavia kokonaislukuja. Tällöin seuraavat pätevät:
(e) jos 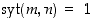 sekä
sekä 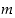 ja
ja 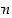 ovat molemmat luvun
ovat molemmat luvun 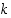 tekijöitä, myös tulo
tekijöitä, myös tulo 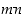 on luvun
on luvun 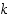 tekijä.
tekijä.
Opiskelutehtävä 17. (Tulon jakaminen)
Olkoot 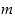 ja
ja 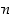 keskenään jaottomia kokonaislukuja sekä kokonaisluku
keskenään jaottomia kokonaislukuja sekä kokonaisluku 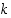 sellainen, että
sellainen, että 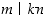 . Osoita, että tällöin
. Osoita, että tällöin 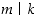 .
.
Suurin yhteinen tekijä voidaan määritellä luontevasti myös useammalle kuin kahdelle luvulle: se on kaikille yhteisistä positiivisista tekijöistä suurin, tai se on yhteisistä positiivisista tekijöistä se, joka on jaollinen kaikilla muilla yhteisillä tekijöillä. Monen luvun yhteisen tekijän etsiminen voidaan aina palauttaa kahden luvun yhteisten tekijöiden määräämisiin. Esimerkiksi kolmelle luvulle 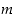 ,
,
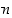 ja
ja 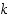 pätee, että
pätee, että
Nollasta eroaville kokonaisluvuille 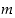 ja
ja 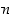 voidaan myös määritellä
pienin yhteinen jaettava (pyj). Se on positiivinen kokonaisluku
voidaan myös määritellä
pienin yhteinen jaettava (pyj). Se on positiivinen kokonaisluku 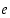 ,
jolle on voimassa ehdot
,
jolle on voimassa ehdot
On selvää, että aina 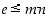 ,
mutta pienin yhteinen jaettava voi olla tätä tuloa pienempikin. Esimerkiksi lukujen 12 ja 18 pienin yhteinen jaettava on 36.
,
mutta pienin yhteinen jaettava voi olla tätä tuloa pienempikin. Esimerkiksi lukujen 12 ja 18 pienin yhteinen jaettava on 36.
Voidaan osoittaa, että pienimmälle yhteiselle jaettavalle 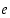 pätee yhtälö
pätee yhtälö 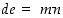 ,
kun
,
kun 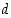 on kyseisten lukujen suurin yhteinen tekijä. Pienimmän yhteisen jaettavan laskeminen palautuukin siis kaavalla
on kyseisten lukujen suurin yhteinen tekijä. Pienimmän yhteisen jaettavan laskeminen palautuukin siis kaavalla
suurimman yhteisen tekijän määräämiseen.
1. Määrää lukujen 2279 ja 989 suurin yhteinen tekijä.
2. Osoita, että 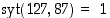 ,
ja määrää jotkin sellaiset kokonaisluvut
,
ja määrää jotkin sellaiset kokonaisluvut 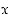 ja
ja 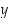 ,
että
,
että 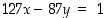 .
.
3. Oletetaan, että kokonaisluku 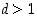 on sellainen, että jollekin kokonaisluvulle
on sellainen, että jollekin kokonaisluvulle 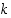 sekä
sekä 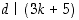 että
että 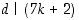 . Osoita, että tällöin
. Osoita, että tällöin 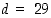 .
.
4. Olkoot 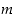 ja
ja 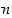 nollasta eroavia kokonaislukuja ja
nollasta eroavia kokonaislukuja ja 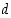 niiden suurin yhteinen tekijä. Osoita, että kokonaisluvut
niiden suurin yhteinen tekijä. Osoita, että kokonaisluvut 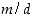 ja
ja 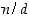 ovat keskenään jaottomia.
ovat keskenään jaottomia.
5. Tarkastellaan, milloin ns.
Diofantoksen yhtälöllä 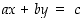 ,
missä
,
missä 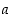 ,
,
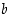 ja
ja 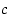 ovat kokonaislukuja, on kokonaislukuratkaisuja
ovat kokonaislukuja, on kokonaislukuratkaisuja 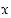 ja
ja 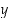 . Olkoon
. Olkoon 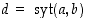 . Osoita, että edellä oleva Diofantoksen yhtälö ratkeaa täsmälleen silloin kun
. Osoita, että edellä oleva Diofantoksen yhtälö ratkeaa täsmälleen silloin kun 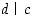 .
.