Tehtävän 22 ratkaisu
Ratkaisua alkutekijäjakoon voidaan lähteä hakemaan yksinkertaisesti kokeilemalla millä alkuluvuilla annetun luvun voi jakaa niin, että jako menee tasan ja kuinka monta kertaa kullakin alkuluvulla voidaan jakaa.
Aloitetaan kakkosesta, joka on alkuluku, ja jaetaan annettu luku sillä. Jos jako menee tasan (eli jakojäännös on 0), jakaa luku 2 annetun luvun. Kokeillaan saadun tekijän jakamista kakkosella niin kauan kuin jako menee tasan. Kun jako ei enää mene tasan, yritetään sitten jakaa alkuluvulla 3. Jatketaan näin yhä suuremmilla alkuluvuilla kunnes alkutekijäesitys on löydetty (ks. satasta pienemmät alkuluvut opiskelutehtävästä 19).
Edellisessä opiskelutehtävässä 21 osoitettiin, että jos positiivinen kokonaisluku 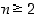 ei ole alkuluku, niin on olemassa alkuluku
p siten, että
ei ole alkuluku, niin on olemassa alkuluku
p siten, että 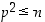 ja
ja 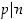 . Kurssin alussa käsiteltyjen logiikan säännön
. Kurssin alussa käsiteltyjen logiikan säännön 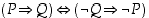 (ks. lause 1.2.3) mukaan tämä on yhtäpitävää sen kanssa, että jos tällaista alkulukua
p ei ole olemassa, on luvun
n oltava alkuluku. Tästä seuraa, että jaettaessa lukua
n alkutekijöihin, ei sitä tarvitse yrittää jakaa lukua
(ks. lause 1.2.3) mukaan tämä on yhtäpitävää sen kanssa, että jos tällaista alkulukua
p ei ole olemassa, on luvun
n oltava alkuluku. Tästä seuraa, että jaettaessa lukua
n alkutekijöihin, ei sitä tarvitse yrittää jakaa lukua 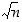 suuremmilla alkuluvuilla. Esimerkiksi, jos jaetaan lukua 132 alkutekijöihin, ei eri alkuluvuilla jakamista tarvitse kokeilla lukua
suuremmilla alkuluvuilla. Esimerkiksi, jos jaetaan lukua 132 alkutekijöihin, ei eri alkuluvuilla jakamista tarvitse kokeilla lukua 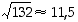 eli alkulukua 11 suuremmilla alkuluvuilla.
eli alkulukua 11 suuremmilla alkuluvuilla.
Siirrytään nyt itse tehtävän ratkaisemiseen. Ensinnäkin
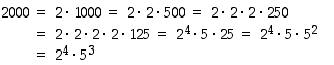
Luku 2001 ei parittomana selvästikään ole jaollinen luvulla 2, mutta kolmosella kylläkin. (Ennakkotietoa modulolaskennasta: tämän voi päätellä siitä, että luvun numeroiden summa 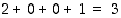 on jaollinen kolmosella, joten luku itsekin on kolmosen jaollisuustestin nojalla jaollinen kolmosella, ks. Jaollisuustestejä.) Laskemalla jakolasku saadaan
on jaollinen kolmosella, joten luku itsekin on kolmosen jaollisuustestin nojalla jaollinen kolmosella, ks. Jaollisuustestejä.) Laskemalla jakolasku saadaan 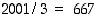 . Mikäli 667 on yhdistetty luku, on sillä oltava alkutekijä, joka on pienempi tai yhtä suuri kuin
. Mikäli 667 on yhdistetty luku, on sillä oltava alkutekijä, joka on pienempi tai yhtä suuri kuin 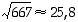 . Riittää siten etsiä alkutekijätekijää, joka on pienempi 25. Jos tällaista ei löydy, on 667 alkuluku ja silloin luvun 2001 alkutekijäesitys on
. Riittää siten etsiä alkutekijätekijää, joka on pienempi 25. Jos tällaista ei löydy, on 667 alkuluku ja silloin luvun 2001 alkutekijäesitys on 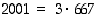 . Kokeilemalla havaitaan kuitenkin, että luku 667 on jaollinen luvulla 23 ja
. Kokeilemalla havaitaan kuitenkin, että luku 667 on jaollinen luvulla 23 ja 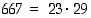 . Näin ollen
. Näin ollen 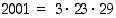 .
.
Tutkitaan sitten lukua 1999. Koska 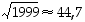 ,
riittää yrittää jakaa luku 1999 lukua 45 pienemmillä alkuluvuilla (ks. alkuluvut opiskelutehtävästä 19). Kokeilemalla jakamista kaikilla tällaisilla alkuluvuilla huomataan, ettei jako mene milloinkaan tasan. Siispä 1999 on alkuluku.
,
riittää yrittää jakaa luku 1999 lukua 45 pienemmillä alkuluvuilla (ks. alkuluvut opiskelutehtävästä 19). Kokeilemalla jakamista kaikilla tällaisilla alkuluvuilla huomataan, ettei jako mene milloinkaan tasan. Siispä 1999 on alkuluku.
Jatketaan vielä tutkimalla luvut 2002, 2003 ja 2006.
Edellä esitettyjä ideoita soveltamalla saadaan, että 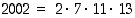 .
.
Tutkitaan sitten lukua 2003. Koska 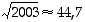 ,
riittää yrittää jakaa luku 2003 lukua 45 pienemmillä alkuluvuilla. Kokeilemalla jakamista kaikilla tällaisilla alkuluvuilla huomataan, ettei jako mene milloinkaan tasan. Siispä 2003 on alkuluku.
,
riittää yrittää jakaa luku 2003 lukua 45 pienemmillä alkuluvuilla. Kokeilemalla jakamista kaikilla tällaisilla alkuluvuilla huomataan, ettei jako mene milloinkaan tasan. Siispä 2003 on alkuluku.
Koska luku 2006 on parillinen, se on jaollinen ainakin kakkosella: 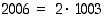 . Nyt täytyy edelleen yrittää jakaa luku 1003 alkutekijöihin eli yrittää jakaa lukua 32 (
. Nyt täytyy edelleen yrittää jakaa luku 1003 alkutekijöihin eli yrittää jakaa lukua 32 (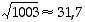 ) pienemmillä alkuluvuilla. Havaitaan, että 17 jakaa luvun 1003, ja siis
) pienemmillä alkuluvuilla. Havaitaan, että 17 jakaa luvun 1003, ja siis 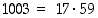 . Näin ollen
. Näin ollen 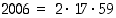 .
.
Lisätietoja. Korkeintaan yksi luvun
n alkutekijä
q voi olla suurempi kuin 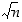 . Tästä seuraa, että kyseinen luku
q saadaan tulokseksi kun
n jaetaan kaikilla sen lukua
. Tästä seuraa, että kyseinen luku
q saadaan tulokseksi kun
n jaetaan kaikilla sen lukua 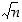 pienemmillä alkutekijöillä.
Mieti miksi edellinen pätee!
pienemmillä alkutekijöillä.
Mieti miksi edellinen pätee!
Lisätehtävä. Jos olet kiinnostunut ohjelmoinnista, kokeile kirjoittaa ohjelma, joka jakaa annetun positiivisen kokonaisluvun alkutekijöihinsä. Keksi erilaisia toteutuksia alkutekijöiden etsimiselle ja kokeile mikä toteutuksista näyttäisi olevan nopein. Kokeile kirjoittaa ohjelma vaikkapa graafiselle laskimellesi tai tee siitä nettiversio. Nettiversiosta voit tehdä joko selaimessa suoritettavan käyttämällä JavaScriptiä tai palvelimella suoritettavan hyödyntämällä jotain palvelinpuolen ohjelmointikieleltä, kuten PHP:ta, JSP:tä, Perl:iä, Pythonia tai ASP:tä.
Linkkejä:
Alkutekijöihin jako: http://en.wikipedia.org/wiki/Integer_factorization
Mathematica: http://mathworld.wolfram.com/PrimeFactorization.html
[Opiskelutehtävä 22] [Vinkki tehtävään 22]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
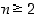 ei ole alkuluku, niin on olemassa alkuluku
p siten, että
ei ole alkuluku, niin on olemassa alkuluku
p siten, että 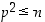 ja
ja 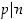 . Kurssin alussa käsiteltyjen logiikan säännön
. Kurssin alussa käsiteltyjen logiikan säännön 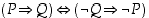 (ks. lause 1.2.3) mukaan tämä on yhtäpitävää sen kanssa, että jos tällaista alkulukua
p ei ole olemassa, on luvun
n oltava alkuluku. Tästä seuraa, että jaettaessa lukua
n alkutekijöihin, ei sitä tarvitse yrittää jakaa lukua
(ks. lause 1.2.3) mukaan tämä on yhtäpitävää sen kanssa, että jos tällaista alkulukua
p ei ole olemassa, on luvun
n oltava alkuluku. Tästä seuraa, että jaettaessa lukua
n alkutekijöihin, ei sitä tarvitse yrittää jakaa lukua 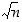 suuremmilla alkuluvuilla. Esimerkiksi, jos jaetaan lukua 132 alkutekijöihin, ei eri alkuluvuilla jakamista tarvitse kokeilla lukua
suuremmilla alkuluvuilla. Esimerkiksi, jos jaetaan lukua 132 alkutekijöihin, ei eri alkuluvuilla jakamista tarvitse kokeilla lukua 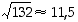 eli alkulukua 11 suuremmilla alkuluvuilla.
eli alkulukua 11 suuremmilla alkuluvuilla.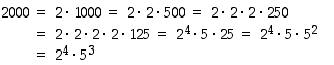
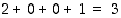 on jaollinen kolmosella, joten luku itsekin on kolmosen jaollisuustestin nojalla jaollinen kolmosella, ks.
on jaollinen kolmosella, joten luku itsekin on kolmosen jaollisuustestin nojalla jaollinen kolmosella, ks. 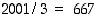 . Mikäli 667 on yhdistetty luku, on sillä oltava alkutekijä, joka on pienempi tai yhtä suuri kuin
. Mikäli 667 on yhdistetty luku, on sillä oltava alkutekijä, joka on pienempi tai yhtä suuri kuin 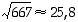 . Riittää siten etsiä alkutekijätekijää, joka on pienempi 25. Jos tällaista ei löydy, on 667 alkuluku ja silloin luvun 2001 alkutekijäesitys on
. Riittää siten etsiä alkutekijätekijää, joka on pienempi 25. Jos tällaista ei löydy, on 667 alkuluku ja silloin luvun 2001 alkutekijäesitys on 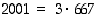 . Kokeilemalla havaitaan kuitenkin, että luku 667 on jaollinen luvulla 23 ja
. Kokeilemalla havaitaan kuitenkin, että luku 667 on jaollinen luvulla 23 ja 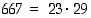 . Näin ollen
. Näin ollen 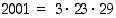 .
.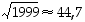 ,
riittää yrittää jakaa luku 1999 lukua 45 pienemmillä alkuluvuilla (ks. alkuluvut opiskelutehtävästä
,
riittää yrittää jakaa luku 1999 lukua 45 pienemmillä alkuluvuilla (ks. alkuluvut opiskelutehtävästä 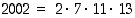 .
.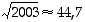 ,
riittää yrittää jakaa luku 2003 lukua 45 pienemmillä alkuluvuilla. Kokeilemalla jakamista kaikilla tällaisilla alkuluvuilla huomataan, ettei jako mene milloinkaan tasan. Siispä 2003 on alkuluku.
,
riittää yrittää jakaa luku 2003 lukua 45 pienemmillä alkuluvuilla. Kokeilemalla jakamista kaikilla tällaisilla alkuluvuilla huomataan, ettei jako mene milloinkaan tasan. Siispä 2003 on alkuluku.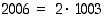 . Nyt täytyy edelleen yrittää jakaa luku 1003 alkutekijöihin eli yrittää jakaa lukua 32 (
. Nyt täytyy edelleen yrittää jakaa luku 1003 alkutekijöihin eli yrittää jakaa lukua 32 (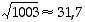 ) pienemmillä alkuluvuilla. Havaitaan, että 17 jakaa luvun 1003, ja siis
) pienemmillä alkuluvuilla. Havaitaan, että 17 jakaa luvun 1003, ja siis 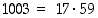 . Näin ollen
. Näin ollen 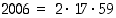 .
.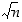 . Tästä seuraa, että kyseinen luku
q saadaan tulokseksi kun
n jaetaan kaikilla sen lukua
. Tästä seuraa, että kyseinen luku
q saadaan tulokseksi kun
n jaetaan kaikilla sen lukua 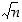 pienemmillä alkutekijöillä.
Mieti miksi edellinen pätee!
pienemmillä alkutekijöillä.
Mieti miksi edellinen pätee!