I.2. Lauselogiikkaa
Matematiikassa aksioomat ja lauseet ovat luonteeltaan
väitteitä,
propositioita. Niille on ominaista, että ne ovat aina joko tosia (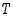 ) tai epätosia (
) tai epätosia (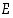 ), ne ovat siis
kaksiarvoisia. Esimerkiksi lausumat "
), ne ovat siis
kaksiarvoisia. Esimerkiksi lausumat "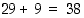 " ja "
" ja "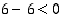 " ovat tällaisia väitelauseita, sen sijaan ilmaisu "
" ovat tällaisia väitelauseita, sen sijaan ilmaisu "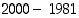 " ei ole, koska se ei edes väitä mitään. Kullakin lauseella
" ei ole, koska se ei edes väitä mitään. Kullakin lauseella 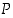 ,
,
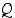 ,
… on siis totuusarvonaan joko
,
… on siis totuusarvonaan joko 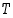 tai
tai 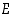 . Lausumaa, jonka totuusarvo riippuu jostain muuttujasta, sanotaan
avoimeksi
lauseeksi. Esimerkiksi lauseen "
. Lausumaa, jonka totuusarvo riippuu jostain muuttujasta, sanotaan
avoimeksi
lauseeksi. Esimerkiksi lauseen "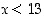 " totuusarvo riippuu muuttujan
" totuusarvo riippuu muuttujan 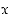 suuruudesta; sillä ei ole totuusarvoa ennenkuin muuttujalle annetaan arvo. Avoimia lauseita käsitellään lähemmin seuraavassa pykälässä.
suuruudesta; sillä ei ole totuusarvoa ennenkuin muuttujalle annetaan arvo. Avoimia lauseita käsitellään lähemmin seuraavassa pykälässä.
Väitelauseista voidaan muodostaa uusia lauseita ns.
loogisten
siteiden eli
konnektiivien avulla. Ne ovat lauseiden väliin lisättäviä sidesanoja tai merkkejä, joista yleisimpiä ovat ¬, ∧, ∨, ⇒ ja ⇔, ja jotka selitetään tarkemmin seuraavassa.
Negaatio eli
vastakohta (¬). Lauseen 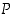 negaatio on sen vastaväite
negaatio on sen vastaväite  ,
joka määritellään yksinkertaisesti seuraavalla
totuustaulukolla.
,
joka määritellään yksinkertaisesti seuraavalla
totuustaulukolla.
Siinä taulukoidaan, miten lauseen
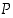 totuusarvosta saadaan lauseen
totuusarvosta saadaan lauseen 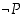 totuusarvo. Negaatio vaihtaa siis lauseen totuusarvon päinvastaiseksi. Esimerkiksi lauseen "
totuusarvo. Negaatio vaihtaa siis lauseen totuusarvon päinvastaiseksi. Esimerkiksi lauseen "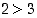 " negaatio on lause "
" negaatio on lause "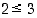 ".
".
Konjunktio eli "
ja" (∧). Lauseiden 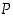 ja
ja 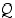 konjunktio
konjunktio 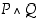 on tosi täsmälleen silloin, kun sekä
on tosi täsmälleen silloin, kun sekä 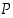 että
että 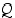 ovat tosia.
ovat tosia.
Se määritellään siis seuraavalla totuustaulukolla, jossa taulukoidaan nyt, miten atomilauseiden 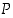 ja
ja 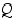 mahdollisista totuusarvoista saadaan yhdistetyn lauseen eli molekyylilauseen
mahdollisista totuusarvoista saadaan yhdistetyn lauseen eli molekyylilauseen 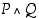 totuusarvo. Merkin "∧" sijasta käytetään myös et-merkkiä "&".
totuusarvo. Merkin "∧" sijasta käytetään myös et-merkkiä "&".
Disjunktio eli "
tai" (∨). Lauseiden 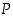 ja
ja 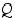 disjunktio
disjunktio 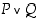 on tosi täsmälleen silloin, kun
on tosi täsmälleen silloin, kun 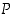 on tosi tai
on tosi tai 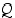 on tosi tai molemmat ovat tosia.
on tosi tai molemmat ovat tosia.
Huomaa tässä tai-sanan merkitys: kyseessä ei ole poissulkeva "tai" eli kyseessä ei ole "joko − tai", vaan 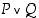 on tosi myös silloin, kun molemmat yhdistettävät lauseet ovat tosia.
on tosi myös silloin, kun molemmat yhdistettävät lauseet ovat tosia.
Implikaatio eli
seuraus (⇒). Kun 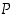 ja
ja 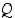 ovat lauseita, tarkoittaa
ovat lauseita, tarkoittaa 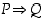 lausetta "jos
lausetta "jos 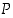 pätee, niin
pätee, niin 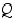 pätee" tai "
pätee" tai "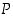 :stä seuraa
:stä seuraa 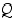 " ja sen totuusarvo määritellään seuraavan totuustaulukon avulla.
" ja sen totuusarvo määritellään seuraavan totuustaulukon avulla.
Huomaa, että jos 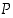 on epätosi, lause
on epätosi, lause 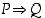 on tosi riippumatta lauseen
on tosi riippumatta lauseen 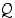 totuusarvosta. Esimerkiksi lause "
totuusarvosta. Esimerkiksi lause "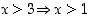 " on tosi sijoitettiinpa luvun
" on tosi sijoitettiinpa luvun
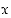 paikalle mikä kokonaisluku tahansa. Sen sijaan lause "
paikalle mikä kokonaisluku tahansa. Sen sijaan lause "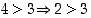 " ei ole tosi.
" ei ole tosi.
Ekvivalenssi eli
yhtäpitävyys (⇔). Kun 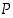 ja
ja 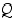 ovat lauseita, tarkoittaa
ovat lauseita, tarkoittaa  ,
että lauseet
,
että lauseet 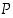 ja
ja 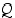 ovat yhtäpitäviä ts.
ovat yhtäpitäviä ts. 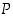 ja
ja 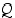 pätevät yhtaikaa, ja sen totuusarvo määritellään seuraavan totuustaulukon mukaan.
pätevät yhtaikaa, ja sen totuusarvo määritellään seuraavan totuustaulukon mukaan.
Kun  on tosi, eli kun lauseilla
on tosi, eli kun lauseilla 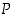 ja
ja 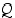 on samat totuusarvot, sanotaan myös, että lauseet
on samat totuusarvot, sanotaan myös, että lauseet 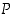 ja
ja 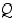 ovat
loogisesti
ekvivalentit. Esimerkiksi lause "
ovat
loogisesti
ekvivalentit. Esimerkiksi lause "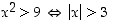 " on tosi kaikilla reaaliluvun
" on tosi kaikilla reaaliluvun 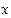 arvoilla.
arvoilla.
Jos useita lauseita yhdistetään erilaisilla konnektiiveilla, on selvyyden vuoksi käytettävä apuna sulkeita osoittamaan yhdistelyjärjestykset. Seuraavassa esimerkissä on tehty näin.
Esimerkki 1.2.1.
Verrataan lauseiden 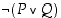 ja
ja 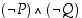 totuusarvoja keskenään. Tehdään seuraavanlainen taulukko.
totuusarvoja keskenään. Tehdään seuraavanlainen taulukko.
Taulukosta havaitaan, että lauseiden 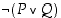 ja
ja 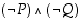 totuusarvot ovat aina samat riippumatta atomilauseiden
totuusarvot ovat aina samat riippumatta atomilauseiden 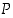 ja
ja 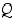 totuusarvoista. Tämän mukaan ekvivalenssilause
totuusarvoista. Tämän mukaan ekvivalenssilause 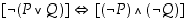 on identtisesti tosi.
on identtisesti tosi.

Lukujen kerto- ja yhteenlaskuista kertolasku on perinteisesti 'vahvempi', ts. se suoritetaan lausekkeissa ennen yhteenlaskua. Siksi esimerkiksi lausekkeesta 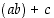 voidaan jättää sulut pois. Vastaavasti loogisille siteillekin sovitaan
suoritusjärjestykset. Niistä negaatio (¬) on vahvin, seuraavaksi konjunktio (∧) ja disjunktio (∨) keskenään yhtä vahvoina, sitten implikaatio (⇒) ja lopuksi ekvivalenssi (⇔) heikoimpana. Yllä olevan esimerkin 1.2.1 lauseke
voidaan jättää sulut pois. Vastaavasti loogisille siteillekin sovitaan
suoritusjärjestykset. Niistä negaatio (¬) on vahvin, seuraavaksi konjunktio (∧) ja disjunktio (∨) keskenään yhtä vahvoina, sitten implikaatio (⇒) ja lopuksi ekvivalenssi (⇔) heikoimpana. Yllä olevan esimerkin 1.2.1 lauseke
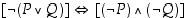
voidaan siten kirjoittaa vähemmin sulkein muodossa
 .
.
Esimerkki 1.2.2.
Verrataan lauseiden 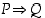 ja
ja 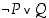 totuusarvoja keskenään. Tehdään seuraavanlainen taulukko.
totuusarvoja keskenään. Tehdään seuraavanlainen taulukko.
Havaitaan, että lauseiden 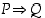 ja
ja 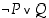 totuusarvot ovat aina samat riippumatta atomilauseiden
totuusarvot ovat aina samat riippumatta atomilauseiden 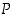 ja
ja 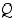 totuusarvoista. Siten lause
totuusarvoista. Siten lause 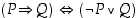 on identtisesti tosi.
on identtisesti tosi.

Edellisten esimerkkien kaltaisia, identtisesti tosia lauseita, sanotaan
tautologioiksi. Seuraavassa lauseessa on eräitä yleisimpiä tautologioita. Ne voidaan todeta päteviksi totuustaulukoiden avulla.
Lause 1.2.3.
Kun 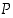 ja
ja 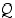 ovat loogisia lauseita, ovat seuraavat tautologioita:
ovat loogisia lauseita, ovat seuraavat tautologioita:
(a) 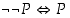 Kaksoiskiellon poisto
Kaksoiskiellon poisto
(b) 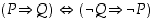 Kontraponointilaki
Kontraponointilaki
(c) 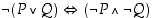 De Morganin 1. laki
De Morganin 1. laki
(d) 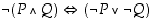 De Morganin 2. laki
De Morganin 2. laki
(e) 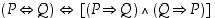 Ekvivalenssilaki
Ekvivalenssilaki
(f) 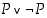 Vaihtoehtopakko
Vaihtoehtopakko
(g) 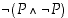 Ristiriidattomuuspakko.
Ristiriidattomuuspakko.
Esimerkiksi ekvivalenssilain mukaan kahden väitteen yhtäpitäväksi osoittaminen voi tapahtua − ja useimmiten myös juuri näin tehdään − osoittamalla ne erikseen toistensa seurauksiksi.
Opiskelutehtävä 1. (Tämä lause on epätosi)
Mieti lausetta "Tämä lause on epätosi". Onko se tosi vai epätosi?
Vinkki tehtävään 1
Opiskelutehtävä 2. (Implikaation vastaväite)
Osoita totuustaulukon avulla, että lauseen 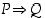 vastaväite on
vastaväite on 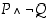 . Osoita sama myös käyttäen esimerkkiä 1.2.2 ja lausetta 1.2.3 hyväksi.
. Osoita sama myös käyttäen esimerkkiä 1.2.2 ja lausetta 1.2.3 hyväksi.
Vinkki tehtävään 2
Opiskelutehtävä 3. (Ekvivalentit lauseet)
a) Osoita seuraavat lauseet loogisesti ekvivalenteiksi:
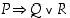 ,
,
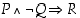 ja
ja 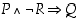 .
.
b) Käyttäen a)-kohdan ekvivalentteja muotoja lausu väite "Jaoton kokonaisluku on pariton tai kakkonen" kahdella muulla tavalla.
Vinkki tehtävään 3
Opiskelutehtävä 4. (Loogisen lauseen sievennys)
Sievennä lauseke 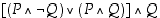 .
.
Vinkki tehtävään 4
Seuraaviin tautologioihin perustuvat yleisimmät matematiikan todistustavat. Näidenkin todistukset voidaan tehdä totuustaulukoilla.
Lause 1.2.4.
Kun 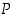 ,
,
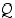 ja
ja 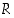 ovat logiikan lauseita, ovat seuraavat tautologioita:
ovat logiikan lauseita, ovat seuraavat tautologioita:
(a) 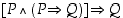 Suora päättely
Suora päättely
(b) 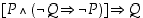 Käänteinen suora päättely
Käänteinen suora päättely
(c) 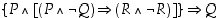 Epäsuora päättely
Epäsuora päättely
Suora päättely on näistä selkein ja tavanomaisin, jossa siis lauseesta 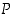 ,
oletuksesta, pyritään suoraan lauseeseen
,
oletuksesta, pyritään suoraan lauseeseen 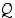 ,
väitteeseen.
,
väitteeseen.
Kontraponointilain mukaan lause 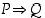 voidaan korvata lauseella
voidaan korvata lauseella 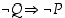 . Tällöin suorasta päättelystä saadaan käänteinen suora päättely, missä siis
vastaväitteestä eli
antiteesistä
. Tällöin suorasta päättelystä saadaan käänteinen suora päättely, missä siis
vastaväitteestä eli
antiteesistä 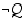 johdetaan oletuksen vastakohta
johdetaan oletuksen vastakohta 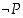 . Jos tässä ajattelemme oletuksen olevan toden, seuraa siitä, että oletus ja sen vastakohta eivät voi olla yhtaikaa voimassa, se, että vastaväite ei ole tosi, vaan sen vastakohta eli siis itse väite on tosi. On kuitenkin huomattava, että päättelyn on toimittava kaikilla totuusarvoilla, jotta voimme tehdä päätelmiä myös hypoteeseista, joiden todellista totuusarvoa emme etukäteen tiedä.
. Jos tässä ajattelemme oletuksen olevan toden, seuraa siitä, että oletus ja sen vastakohta eivät voi olla yhtaikaa voimassa, se, että vastaväite ei ole tosi, vaan sen vastakohta eli siis itse väite on tosi. On kuitenkin huomattava, että päättelyn on toimittava kaikilla totuusarvoilla, jotta voimme tehdä päätelmiä myös hypoteeseista, joiden todellista totuusarvoa emme etukäteen tiedä.
Epäsuorassa päättelyssä vastaväitteestä 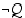 johdetaan oletuksen
johdetaan oletuksen 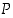 avulla jokin identtisesti epätosi lause
avulla jokin identtisesti epätosi lause 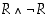 ,
ristiriita eli
kontradiktio. Käänteinen suora päättely on eräs epäsuoran päättelyn alalaji, sillä siinä lause
,
ristiriita eli
kontradiktio. Käänteinen suora päättely on eräs epäsuoran päättelyn alalaji, sillä siinä lause 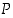 on lauseen
on lauseen 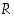 roolissa. Lauseen
roolissa. Lauseen 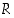 merkitys epäsuorassa päättelyssä on se, että ristiriidan aiheeksi kelpaa mikä tahansa lausuma − muukin kuin oletus
merkitys epäsuorassa päättelyssä on se, että ristiriidan aiheeksi kelpaa mikä tahansa lausuma − muukin kuin oletus
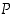 .
.
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
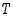 ) tai epätosia (
) tai epätosia (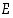 ), ne ovat siis
kaksiarvoisia. Esimerkiksi lausumat "
), ne ovat siis
kaksiarvoisia. Esimerkiksi lausumat "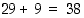 " ja "
" ja "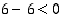 " ovat tällaisia väitelauseita, sen sijaan ilmaisu "
" ovat tällaisia väitelauseita, sen sijaan ilmaisu "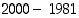 " ei ole, koska se ei edes väitä mitään. Kullakin lauseella
" ei ole, koska se ei edes väitä mitään. Kullakin lauseella 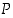 ,
,
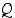 ,
… on siis totuusarvonaan joko
,
… on siis totuusarvonaan joko 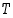 tai
tai 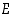 . Lausumaa, jonka totuusarvo riippuu jostain muuttujasta, sanotaan
avoimeksi
lauseeksi. Esimerkiksi lauseen "
. Lausumaa, jonka totuusarvo riippuu jostain muuttujasta, sanotaan
avoimeksi
lauseeksi. Esimerkiksi lauseen "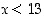 " totuusarvo riippuu muuttujan
" totuusarvo riippuu muuttujan 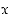 suuruudesta; sillä ei ole totuusarvoa ennenkuin muuttujalle annetaan arvo. Avoimia lauseita käsitellään lähemmin seuraavassa pykälässä.
suuruudesta; sillä ei ole totuusarvoa ennenkuin muuttujalle annetaan arvo. Avoimia lauseita käsitellään lähemmin seuraavassa pykälässä. 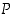
 ,
joka määritellään yksinkertaisesti seuraavalla
totuustaulukolla
,
joka määritellään yksinkertaisesti seuraavalla
totuustaulukolla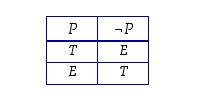
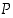 totuusarvosta saadaan lauseen
totuusarvosta saadaan lauseen 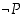 totuusarvo. Negaatio vaihtaa siis lauseen totuusarvon päinvastaiseksi. Esimerkiksi lauseen "
totuusarvo. Negaatio vaihtaa siis lauseen totuusarvon päinvastaiseksi. Esimerkiksi lauseen "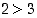 " negaatio on lause "
" negaatio on lause "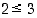 ".
". 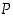 ja
ja 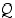
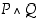 on tosi täsmälleen silloin, kun sekä
on tosi täsmälleen silloin, kun sekä 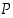 että
että 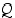 ovat tosia.
ovat tosia. 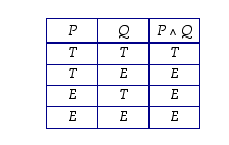
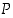 ja
ja 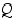 mahdollisista totuusarvoista saadaan yhdistetyn lauseen eli molekyylilauseen
mahdollisista totuusarvoista saadaan yhdistetyn lauseen eli molekyylilauseen 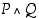 totuusarvo. Merkin "∧" sijasta käytetään myös et-merkkiä "&".
totuusarvo. Merkin "∧" sijasta käytetään myös et-merkkiä "&". 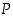 ja
ja 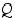
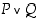 on tosi täsmälleen silloin, kun
on tosi täsmälleen silloin, kun 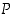 on tosi tai
on tosi tai 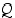 on tosi tai molemmat ovat tosia.
on tosi tai molemmat ovat tosia. 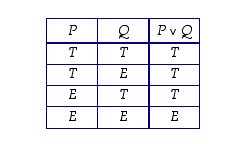
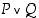 on tosi myös silloin, kun molemmat yhdistettävät lauseet ovat tosia.
on tosi myös silloin, kun molemmat yhdistettävät lauseet ovat tosia. 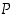 ja
ja 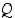 ovat lauseita, tarkoittaa
ovat lauseita, tarkoittaa 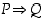 lausetta "jos
lausetta "jos 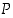 pätee, niin
pätee, niin 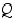 pätee" tai "
pätee" tai "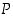 :stä seuraa
:stä seuraa 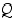 " ja sen totuusarvo määritellään seuraavan totuustaulukon avulla.
" ja sen totuusarvo määritellään seuraavan totuustaulukon avulla. 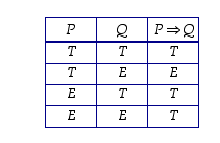
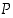 on epätosi, lause
on epätosi, lause 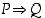 on tosi riippumatta lauseen
on tosi riippumatta lauseen 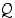 totuusarvosta. Esimerkiksi lause "
totuusarvosta. Esimerkiksi lause "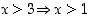 " on tosi sijoitettiinpa luvun
" on tosi sijoitettiinpa luvun
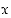 paikalle mikä kokonaisluku tahansa. Sen sijaan lause "
paikalle mikä kokonaisluku tahansa. Sen sijaan lause "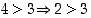 " ei ole tosi.
" ei ole tosi. 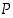 ja
ja 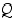 ovat lauseita, tarkoittaa
ovat lauseita, tarkoittaa  ,
että lauseet
,
että lauseet 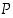 ja
ja 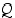 ovat yhtäpitäviä ts.
ovat yhtäpitäviä ts. 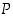 ja
ja 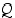 pätevät yhtaikaa, ja sen totuusarvo määritellään seuraavan totuustaulukon mukaan.
pätevät yhtaikaa, ja sen totuusarvo määritellään seuraavan totuustaulukon mukaan. 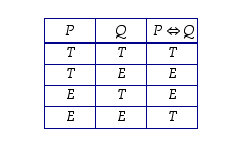
 on tosi, eli kun lauseilla
on tosi, eli kun lauseilla 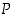 ja
ja 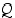 on samat totuusarvot, sanotaan myös, että lauseet
on samat totuusarvot, sanotaan myös, että lauseet 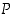 ja
ja 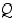 ovat
loogisesti
ovat
loogisesti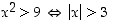 " on tosi kaikilla reaaliluvun
" on tosi kaikilla reaaliluvun 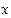 arvoilla.
arvoilla. 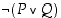 ja
ja 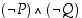 totuusarvoja keskenään. Tehdään seuraavanlainen taulukko.
totuusarvoja keskenään. Tehdään seuraavanlainen taulukko. 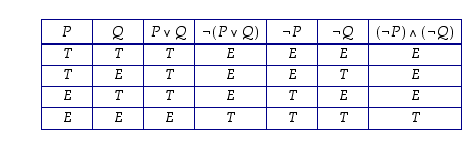
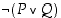 ja
ja 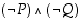 totuusarvot ovat aina samat riippumatta atomilauseiden
totuusarvot ovat aina samat riippumatta atomilauseiden 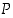 ja
ja 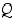 totuusarvoista. Tämän mukaan ekvivalenssilause
totuusarvoista. Tämän mukaan ekvivalenssilause 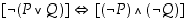 on identtisesti tosi.
on identtisesti tosi. 
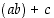 voidaan jättää sulut pois. Vastaavasti loogisille siteillekin sovitaan
suoritusjärjestykset
voidaan jättää sulut pois. Vastaavasti loogisille siteillekin sovitaan
suoritusjärjestykset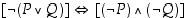
 .
. 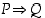 ja
ja 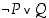 totuusarvoja keskenään. Tehdään seuraavanlainen taulukko.
totuusarvoja keskenään. Tehdään seuraavanlainen taulukko. 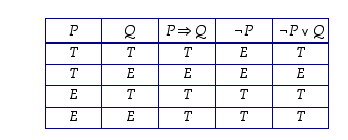
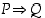 ja
ja 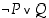 totuusarvot ovat aina samat riippumatta atomilauseiden
totuusarvot ovat aina samat riippumatta atomilauseiden 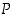 ja
ja 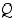 totuusarvoista. Siten lause
totuusarvoista. Siten lause 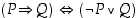 on identtisesti tosi.
on identtisesti tosi. 
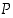 ja
ja 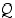 ovat loogisia lauseita, ovat seuraavat tautologioita:
ovat loogisia lauseita, ovat seuraavat tautologioita: 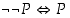
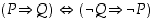 Kontraponointilaki
Kontraponointilaki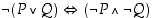
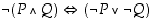 De Morganin 2. laki
De Morganin 2. laki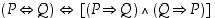 Ekvivalenssilaki
Ekvivalenssilaki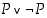 Vaihtoehtopakko
Vaihtoehtopakko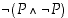 Ristiriidattomuuspakko
Ristiriidattomuuspakko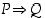 vastaväite on
vastaväite on 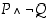 . Osoita sama myös käyttäen esimerkkiä
. Osoita sama myös käyttäen esimerkkiä 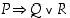 ,
,
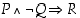 ja
ja 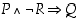 .
. 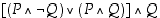 .
. 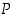 ,
,
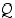 ja
ja 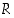 ovat logiikan lauseita, ovat seuraavat tautologioita:
ovat logiikan lauseita, ovat seuraavat tautologioita: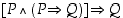
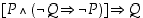
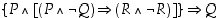
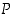 ,
oletuksesta
,
oletuksesta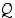 ,
väitteeseen
,
väitteeseen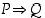 voidaan korvata lauseella
voidaan korvata lauseella 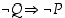 . Tällöin suorasta päättelystä saadaan käänteinen suora päättely, missä siis
vastaväitteestä
. Tällöin suorasta päättelystä saadaan käänteinen suora päättely, missä siis
vastaväitteestä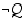 johdetaan oletuksen vastakohta
johdetaan oletuksen vastakohta 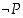 . Jos tässä ajattelemme oletuksen olevan toden, seuraa siitä, että oletus ja sen vastakohta eivät voi olla yhtaikaa voimassa, se, että vastaväite ei ole tosi, vaan sen vastakohta eli siis itse väite on tosi. On kuitenkin huomattava, että päättelyn on toimittava kaikilla totuusarvoilla, jotta voimme tehdä päätelmiä myös hypoteeseista, joiden todellista totuusarvoa emme etukäteen tiedä.
. Jos tässä ajattelemme oletuksen olevan toden, seuraa siitä, että oletus ja sen vastakohta eivät voi olla yhtaikaa voimassa, se, että vastaväite ei ole tosi, vaan sen vastakohta eli siis itse väite on tosi. On kuitenkin huomattava, että päättelyn on toimittava kaikilla totuusarvoilla, jotta voimme tehdä päätelmiä myös hypoteeseista, joiden todellista totuusarvoa emme etukäteen tiedä. 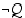 johdetaan oletuksen
johdetaan oletuksen 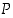 avulla jokin identtisesti epätosi lause
avulla jokin identtisesti epätosi lause 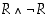 ,
ristiriita
,
ristiriita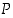 on lauseen
on lauseen 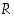 roolissa. Lauseen
roolissa. Lauseen 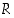 merkitys epäsuorassa päättelyssä on se, että ristiriidan aiheeksi kelpaa mikä tahansa lausuma − muukin kuin oletus
merkitys epäsuorassa päättelyssä on se, että ristiriidan aiheeksi kelpaa mikä tahansa lausuma − muukin kuin oletus
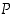 .
. 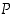 = "on olemassa joukko
= "on olemassa joukko
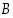 ,
jolle
,
jolle 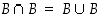 " ja
" ja 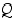 = "kaikille joukoille
= "kaikille joukoille
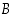 on
on 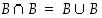 " negaatiot. Mitkä näistä ovat tosia ja mitkä epätosia? (Joukkojen leikkausten ja yhdisteiden määrittelyt kerrataaan pykälässä
" negaatiot. Mitkä näistä ovat tosia ja mitkä epätosia? (Joukkojen leikkausten ja yhdisteiden määrittelyt kerrataaan pykälässä 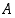 ja
ja
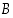 toisessa on palkinto. Laatikon
toisessa on palkinto. Laatikon
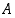 päällä lukee "Laatikon
päällä lukee "Laatikon
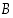 teksti on oikein, ja palkinto on tässä laatikossa." Laatikon
teksti on oikein, ja palkinto on tässä laatikossa." Laatikon
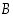 päällä taas lukee "Laatikon
päällä taas lukee "Laatikon
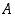 teksti on väärin, ja palkinto on laatikossa
teksti on väärin, ja palkinto on laatikossa
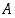 ." Kummassakohan laatikossa palkinto on?
." Kummassakohan laatikossa palkinto on? 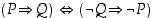 tautologiaksi täyttämällä seuraava totuustaulukko.
tautologiaksi täyttämällä seuraava totuustaulukko. 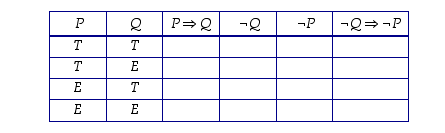
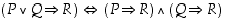 .
. 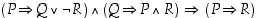 .
.