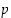 ,
joka on jaollinen vain luvuilla 1, −1,
,
joka on jaollinen vain luvuilla 1, −1, 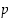 ja
ja 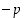 ,
sanotaankin
alkuluvuksi eli
jaottomaksi luvuksi. Muut ykköstä isommat kokonaisluvut ovat
yhdistettyjä lukuja (tai
jaollisia lukuja). Ne ovat silloin muotoa
,
sanotaankin
alkuluvuksi eli
jaottomaksi luvuksi. Muut ykköstä isommat kokonaisluvut ovat
yhdistettyjä lukuja (tai
jaollisia lukuja). Ne ovat silloin muotoa 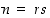 ,
missä
,
missä 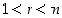 ja
ja 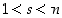 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Jokainen nollasta eroava kokonaisluku on aina jaollinen luvulla 1 ja itsellään sekä näiden vastaluvuilla. Välttämättä luvulla ei olekaan muita tekijöitä. Ykköstä suurempaa kokonaislukua 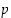 ,
joka on jaollinen vain luvuilla 1, −1,
,
joka on jaollinen vain luvuilla 1, −1, 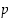 ja
ja 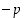 ,
sanotaankin
alkuluvuksi eli
jaottomaksi luvuksi. Muut ykköstä isommat kokonaisluvut ovat
yhdistettyjä lukuja (tai
jaollisia lukuja). Ne ovat silloin muotoa
,
sanotaankin
alkuluvuksi eli
jaottomaksi luvuksi. Muut ykköstä isommat kokonaisluvut ovat
yhdistettyjä lukuja (tai
jaollisia lukuja). Ne ovat silloin muotoa 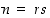 ,
missä
,
missä 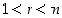 ja
ja 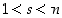 .
.
Alkulukuja ovat mm. 2, 3, 5, 7, 11, 13, 17 ja 19. Pienet alkuluvut voi löytää suhteellisen helposti ns. Eratostheneen seulalla. Esimerkkinä menetelmästä määrätään lottoruudukossa esiintyvät alkuluvut (ks. kuviota alla). Ensin hylätään luku 1. Luku 2 on ensimmäinen alkuluku, ja sen jälkeen viivataan yli kaikki sen monikerrat. Tämän jälkeen ensimmäinen luku, jota ei ole vielä viivattu yli, on seuraava alkuluku, siis luku 3. Taas viivataan yli kaikki tämän monikerrat. Näin jatketaan: Ensimmäinen vastaan tuleva luku, jota ei ole siihen mennessä viivattu yli, on suuruusjärjestyksessä seuraava alkuluku. Sen kaikki monikerrat viivataan sitten yli, jne. Oheisessa kuviossa ympyröidyt luvut ovat tämän menetelmän mukaan lottoruudukossa esiintyvät alkuluvut.
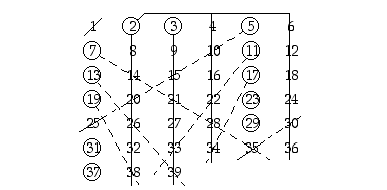
Eratostheneen seulalla voi käsinkin etsiä varsin suuria alkulukuja, aina viisi-kuusinumeroisiin asti. Tietokoneilla päästään tietenkin paljon kauemmaksi! Tällä menetelmällä saadaan siis kaikki tiettyyn lukuun mennessä esiintyvät alkuluvut. Aina ei kuitenkaan tarvita kaikkia perättäisiä alkulukuja, vaan syystä tai toisesta ollaan kiinnostuneita löytämään mahdollisimman suuria alkulukuja. Näihin palataan tämän pykälän lopussa ja RSA-menetelmän yhteydessä (tämän luvun 5. pykälässä).
Opiskelutehtävä 19. (Satasta pienemmät alkuluvut)
Määrää kaikki satasta pienemmät alkuluvut.
Opiskelutehtävä 20. (Alkulukujen muoto)
Osoita, että kaikki lukua 3 suuremmat alkuluvut ovat muotoa 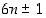 jollekin
jollekin 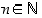 .
.
Alkuluvuilla on jaollisuuden kannalta eräitä tärkeitä erikoisominaisuuksia. Seuraava on perustavanlaatuinen.
Lause 2.4.1. (Eukleideen lemma)
Jos alkuluku 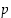 jakaa kahden kokonaisluvun
jakaa kahden kokonaisluvun 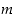 ja
ja 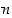 tulon, se jakaa ainakin toisen tulon tekijöistä, ts. jos
tulon, se jakaa ainakin toisen tulon tekijöistä, ts. jos 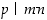 ,
niin
,
niin 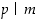 tai
tai 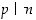 .
.
Todistus. Oletuksen mukaan 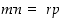 jollekin
jollekin 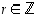 . Jos luku
. Jos luku 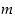 on jaollinen luvulla
on jaollinen luvulla 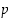 ,
pitää väite paikkansa. Oletetaan sitten, että
,
pitää väite paikkansa. Oletetaan sitten, että 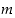 ei ole jaollinen luvulla
ei ole jaollinen luvulla 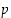 ,
ja osoitetaan, että silloin luku
,
ja osoitetaan, että silloin luku 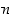 on jaollinen luvulla
on jaollinen luvulla 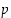 .
.
Koska 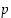 on alkuluku, sillä on positiivisina tekijöinään vain luvut 1 ja
on alkuluku, sillä on positiivisina tekijöinään vain luvut 1 ja 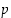 . Toisaalta
. Toisaalta 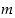 ei ole nyt jaollinen luvulla
ei ole nyt jaollinen luvulla 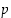 ,
joten välttämättä
,
joten välttämättä 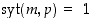 . On siis olemassa esitys
. On siis olemassa esitys 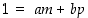 joillekin kokonaisluvuille
joillekin kokonaisluvuille 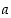 ja
ja 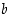 . Kertomalla tämä esitys luvulla
. Kertomalla tämä esitys luvulla 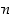 saadaan yhtälö
saadaan yhtälö
mistä näkyykin, että luku 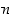 on jaollinen luvulla
on jaollinen luvulla 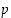 .
.
Osoitetaan, että yhtälöllä 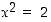 ei ole yhtään rationaalista ratkaisua. Koska kaikkia rationaalilukuja ei voi käydä läpi, lienee viisainta yrittää todistaa väitettä antiteesillä. Oletetaan siis, että
ei ole yhtään rationaalista ratkaisua. Koska kaikkia rationaalilukuja ei voi käydä läpi, lienee viisainta yrittää todistaa väitettä antiteesillä. Oletetaan siis, että 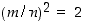 joillekin kokonaisluvuille
joillekin kokonaisluvuille 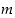 ja
ja 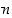 . Voimme olettaa lisäksi, että rationaaliluku
. Voimme olettaa lisäksi, että rationaaliluku 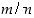 on supistetussa muodossa eli että luvut
on supistetussa muodossa eli että luvut 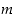 ja
ja 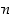 ovat keskenään jaottomia, ts.
ovat keskenään jaottomia, ts. 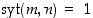 .
.
Yhtälön 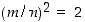 mukaan
mukaan 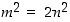 ,
joten tulo
,
joten tulo 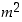 on jaollinen alkuluvulla 2. Eukleideen lemman mukaan silloin
on jaollinen alkuluvulla 2. Eukleideen lemman mukaan silloin 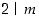 tai
tai 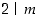 . Joka tapauksessa
. Joka tapauksessa 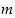 on siis jaollinen luvulla 2, ts.
on siis jaollinen luvulla 2, ts. 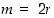 jollekin kokonaisluvulle
jollekin kokonaisluvulle 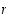 . Siten
. Siten 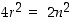 eli
eli 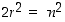 .
.
Vastaavasti kuin edellä päätellään, että 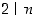 . Mutta nyt luku 2 olisi sekä luvun
. Mutta nyt luku 2 olisi sekä luvun 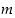 että luvun
että luvun 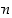 tekijä, mikä on ristiriita näiden keskinäisen jaottomuuden kanssa. Antiteesi on siis epätosi ja väite oikein.
tekijä, mikä on ristiriita näiden keskinäisen jaottomuuden kanssa. Antiteesi on siis epätosi ja väite oikein.
Eukleideen lemmaa ei voi käyttää alkuluvun sijasta yhdistetyille luvuille. Esimerkiksi 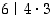 ,
mutta luku 6 ei jaa kumpaakaan tekijää.
,
mutta luku 6 ei jaa kumpaakaan tekijää.
Opiskelutehtävä 21. (Neliöjuurta pienempi alkutekijä)
Osoita, että jos luku 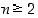 ei ole alkuluku, niin sillä on tekijänä jokin alkuluku
ei ole alkuluku, niin sillä on tekijänä jokin alkuluku 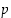 ,
jolle
,
jolle 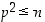 .
.
Lause 2.4.4. (Aritmetiikan peruslause)
Ykköstä suurempi kokonaisluku on joko itse alkuluku tai se on alkulukujen tulo.
Todistus. Tehdään vastaoletus: On olemassa yhdistettyjä positiivisia kokonaislukuja, joita ei voi esittää alkulukujen tulona. Olkoon 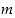 näistä pienin.
näistä pienin.
Yhdistettynä lukuna 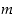 on muotoa
on muotoa 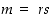 ,
missä
,
missä 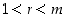 ja
ja 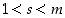 . Koska molemmat luvut
. Koska molemmat luvut 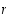 ja
ja 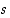 ovat pienempiä kuin
ovat pienempiä kuin 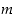 ,
ne ovat joko alkulukuja tai niiden tuloja. Mutta silloinhan myös luku
,
ne ovat joko alkulukuja tai niiden tuloja. Mutta silloinhan myös luku 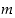 on alkulukujen tulo, vastoin vastaoletusta. Väite on siis oikein.
on alkulukujen tulo, vastoin vastaoletusta. Väite on siis oikein.
Sellaista kokonaisluvun tekijää, joka on alkuluku, sanotaan myös sen alkutekijäksi. Aritmetiikan peruslauseen mukaan jokainen ykköstä suurempi kokonaisluku on itse asiassa esitettävissä muodossa
missä luvut 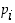 ovat eri alkulukuja,
ovat eri alkulukuja, 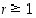 ja potenssit
ja potenssit 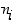 vähintään ykkösiä. Tätä esitystä sanotaan luvun
vähintään ykkösiä. Tätä esitystä sanotaan luvun 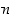 alkutekijäesitykseksi. Jos vielä alkutekijät
alkutekijäesitykseksi. Jos vielä alkutekijät 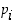 ovat esityksessä pienuusjärjestyksessä, voidaan osoittaa, että esitys on silloin yksikäsitteinen.
ovat esityksessä pienuusjärjestyksessä, voidaan osoittaa, että esitys on silloin yksikäsitteinen.
Opiskelutehtävä 22. (Lukujen alkutekijät)
Jaa luvut 1999, 2000 ja 2001 alkutekijöihinsä.
Jos luvuilla 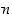 ja
ja 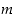 on alkutekijäesitykset
on alkutekijäesitykset
nähdään alkulukujen jaollisuusominaisuuksien perusteella, että luku 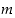 on luvun
on luvun 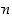 tekijä eli
tekijä eli 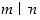 täsmälleen silloin, kun luvun
täsmälleen silloin, kun luvun 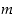 jokainen alkutekijä
jokainen alkutekijä 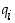 on luvun
on luvun 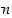 jokin alkutekijä
jokin alkutekijä 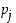 ja sen potenssi
ja sen potenssi 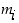 ei ylitä vastaavaa potenssia
ei ylitä vastaavaa potenssia 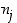 .
.
Kahdelle kokonaisluvulle alkutekijäesityksistä voidaan helposti muodostaa niiden suurin yhteinen tekijä: poimitaan molemmissa esiintyvät alkuluvut, valitaan näille potenssiluvuksi esitysten potensseista pienempi ja muodostetaan näiden tulo. Menettelyn voi induktiivisesti yleistää useammallekin luvulle.
Luvuilla 540, 450 ja 882 on alkutekijäesitykset
joten  . Alkutekijäesityksistä näkyy myös, että mikään näistä luvuista ei jaa toista.
. Alkutekijäesityksistä näkyy myös, että mikään näistä luvuista ei jaa toista.
Tehtävä. Selvitä, kuinka monta eri tekijää on luvuilla 108 ja 25200. (Vihje: Käytä lukujen alkutekijäesityksiä hyväksi.)
Alkulukuja on äärettömän monta.
Todistus. Tehdään vastaoletus (millä muulla tavalla tätä voisi todistaakaan?): alkulukuja on vain äärellinen määrä, olkoot ne 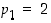 ,
,
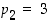 ,
…,
,
…, 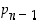 ja
ja 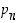 .
.
Tarkastellaan näiden tulosta seuraavaa kokonaislukua eli lukua
Se ei ole jaollinen millään luetellulla alkuluvulla 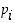 ,
sillä muutoin sellainen alkuluku jakaisi myös luvun 1. Se on siis joko itse alkuluku tai yhdistetty luku, jonka kaikki alkulukutekijät ovat suurempia kuin luetelluista suurin
,
sillä muutoin sellainen alkuluku jakaisi myös luvun 1. Se on siis joko itse alkuluku tai yhdistetty luku, jonka kaikki alkulukutekijät ovat suurempia kuin luetelluista suurin 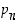 . Joka tapauksessa on siis olemassa alkulukua
. Joka tapauksessa on siis olemassa alkulukua 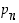 suurempi alkuluku, mikä on vastoin antiteesiä. Lauseen väite on siis oikein.
suurempi alkuluku, mikä on vastoin antiteesiä. Lauseen väite on siis oikein.
Jossain mielessä alkulukuja on kuitenkin vähemmän kuin yhdistettyjä lukuja. Ovathan esimerkiksi kaikki kakkosta suuremmat parilliset luvut yhdistettyjä lukuja. On myös olemassa mielivaltaisen pitkiä yhdistettyjen lukujen muodostamia jonoja. Annetulle luvulle 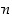 nimittäin luvut
nimittäin luvut 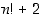 ,
,
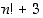 ,
…,
,
…, 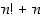 ovat kaikki yhdistettyjä lukuja; ensimmäinen on jaollinen luvulla 2, toinen luvulla 3, …, ja viimeinen luvulla
ovat kaikki yhdistettyjä lukuja; ensimmäinen on jaollinen luvulla 2, toinen luvulla 3, …, ja viimeinen luvulla 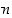 . Näitä peräkkäisiä lukuja on yhteensä
. Näitä peräkkäisiä lukuja on yhteensä 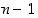 kappaletta.
kappaletta.
Jos 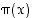 on niiden alkulukujen määrä, jotka ovat korkeintaan luvun
on niiden alkulukujen määrä, jotka ovat korkeintaan luvun 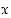 suuruisia, lähestyy ns.
alkulukulauseen mukaan suurilla luvun
suuruisia, lähestyy ns.
alkulukulauseen mukaan suurilla luvun 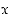 arvoilla siihen mennessä vastaan tulleiden alkulukujen määrän ja lausekkeen
arvoilla siihen mennessä vastaan tulleiden alkulukujen määrän ja lausekkeen 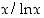 suhde lukua 1 (tässä ln tarkoittaa luonnollista logaritmia). Esimerkiksi luvulle
suhde lukua 1 (tässä ln tarkoittaa luonnollista logaritmia). Esimerkiksi luvulle 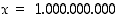 on alkulukujen määrä
on alkulukujen määrä 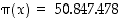 ja lauseke
ja lauseke 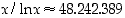 ,
joten niiden suhde on likimain 1,054. Alkulukulauseen todistivat J. Hadamard ja J. C. de la Vallée-Poussin vuonna 1896.
,
joten niiden suhde on likimain 1,054. Alkulukulauseen todistivat J. Hadamard ja J. C. de la Vallée-Poussin vuonna 1896.
Oikein suurelle luvulle voi olla työlästä löytää sen alkutekijäesitystä. Ylivoimaista voi olla jo senkin selvittäminen, onko se yhdistetty luku tai alkuluku. Toisaalta eri tilanteita, esimerkiksi salakirjoitusta, varten halutaan löytää yhä suurempia ja suurempia alkulukuja. Sellaisia etsittiin joskus Fermat'n lukujen
ja nykyään etenkin Mersennen lukujen
joukosta (jälkimmäisistä yleisesti vain alkuluvut numeroidaan, eikä kaikkia kyseisen tyyppisiä lukuja). Pierre de Fermat (1601−1665) itse osoitti, että luvut
ovat alkulukuja ja väitti, että kaikki kyseisen muotoiset luvut olisivat alkulukuja. Mutta Leonhard Euler osoitti v. 1732, että luvulla 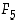 on tekijäesitys
on tekijäesitys
ja I. F. Zolotarov v. 1878, että 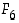 on jaollinen luvulla
on jaollinen luvulla 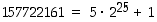 . Nykyään tiedetään, että
. Nykyään tiedetään, että 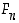 ei ole alkuluku, kun
ei ole alkuluku, kun 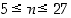 . Luku
. Luku 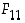 lienee kuitenkin toistaiseksi suurin, jolle tiedetään tekijöihinjako. Alkuluvuiksi Fermat'n luvuista on todettu vain nuo viisi ensimmäistä ja avoin probleema onkin, onko niiden joukossa yhtään muuta.
lienee kuitenkin toistaiseksi suurin, jolle tiedetään tekijöihinjako. Alkuluvuiksi Fermat'n luvuista on todettu vain nuo viisi ensimmäistä ja avoin probleema onkin, onko niiden joukossa yhtään muuta.
Mersennen alkuluvuista ensimmäiset ovat
Vuoden 2006 loppuun mennessä oli löydetty kaikkiaan 44 Mersennen alkulukua. Näistä tiedettiin, että
Tämän lisäksi oli löydetty vielä isommat alkuluvut
mutta niistä ei vielä tiedetty, olivatko ne nimenomaan järjestyksessä seuraavat Mersennen alkuluvut. Viimeisimmän luvun desimaaliesityksessä on yli 9,8 miljoonaa numeroa.
Alkulukuihin liittyy edelleen monia avoimia kysymyksiä. Ei ole esimerkiksi pystytty selvittämään, onko Mersennen alkulukuja ylipäätään olemassa loputtomasti. Avoin kysymys on myös ns.
Goldbachin
väittämä,
jonka mukaan jokainen kakkosta suurempi parillinen luku voidaan esittää kahden alkuluvun summana. Vastausta vaille on edelleen ns.
alkulukukaksosia koskeva pulma: onko olemassa loputtomasti lukupareja 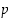 ja
ja 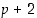 ,
joista molemmat olisivat alkulukuja?
,
joista molemmat olisivat alkulukuja?
Alkulukuihin liittyvää tietoutta, varsinkin uusimmista alkuluvuista, löytyy monilta internetin sivuilta, mm. osoitteesta http://primes.utm.edu/.
1. Määrää kaikki lukua 200 pienemmät alkuluvut.
2. Montako nollaa on kertoman 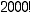 lopussa, jos se kirjoitetaan desimaalimuodossa auki? (Vihje: Nollat tulevat lukujen 2 ja 5 tuloista! Selvitä kysymys ensin pienemmille kertomille.)
lopussa, jos se kirjoitetaan desimaalimuodossa auki? (Vihje: Nollat tulevat lukujen 2 ja 5 tuloista! Selvitä kysymys ensin pienemmille kertomille.)
3. Oletetaan, että alkuluku 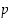 jakaa luvun
jakaa luvun 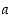 ja summan
ja summan 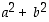 . Osoita, että se jakaa myös luvun
. Osoita, että se jakaa myös luvun 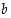 .
.
4. Osoita, että yhtälöllä 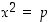 ,
missä
,
missä 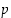 on alkuluku, ei ole yhtään rationaalista ratkaisua.
on alkuluku, ei ole yhtään rationaalista ratkaisua.
5. Osoita, että olkoonpa kokonaisluku 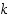 mikä tahansa, ovat luvut
mikä tahansa, ovat luvut 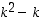 ,
,
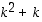 ,
,
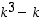 ja
ja 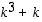 kaikki parillisia.
kaikki parillisia.
6. Määrää lukujen 28665 ja 22869 alkutekijäesitykset ja niiden suurin yhteinen tekijä.
7. Osoita induktiolla, että ns. Fermat'n lukujen 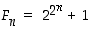 (
( 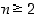 ) desimaaliesitys päättyy aina numeroon 7.
) desimaaliesitys päättyy aina numeroon 7.
8. Onko lukujen 3, 5 ja 7 lisäksi olemassa muita kolmikoita 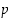 ,
,
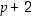 ja
ja 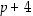 siten, että jokainen näistä kolmesta luvusta on alkuluku?
siten, että jokainen näistä kolmesta luvusta on alkuluku?