[Etusivu] [Sisällysluettelo] [Hakemisto]
[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]

---

Jatkuvuuden määritelmä

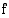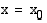Jatkuvuus määritellään tarkemmin raja-arvokäsitteen avulla. Funktio on jatkuva kohdassa , jos

 

Muutoin funktio 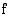on epäjatkuva kohdassa 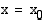. Kohtaa 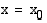kutsutaan tällöin funktion 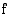epäjatkuvuuskohdaksi.

Huom!

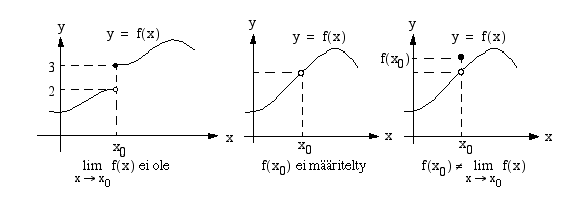
Jotta funktio 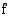olisi jatkuva kohdassa 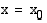, sen on toteutettava kolme ehtoa: funktiolla pitää olla raja-arvo kohdassa 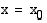, sen on oltava määritelty ko. kohdassa ja funktion raja-arvon ja funktion arvon täytyy olla yhtäsuuret tässä kohdassa. Yllä olevan kuvan ensimmäisellä funktiolla ei ole raja-arvoa kohdasssa 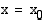ja siksi se on epäjatkuva tässä kohdassa. Toisen kuvan funktion kuvaaja katkeaa kohdassa 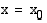, koska funktio ei ole määritelty tässä kohdassa. Kolmannella funktiolla on raja-arvo kohdassa 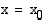ja se on myös määritelty tässä kohdassa, mutta funktion arvon ja raja-arvon ollessa erisuuret, funktio ei kuitenkaan ole jatkuva ko. kohdassa.

Huom!

Edellisen huomautuksen nojalla funktio 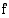on jatkuva kohdassa 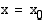, jos on voimassa

 

Ensimmäinen yhtäsuuruus takaa raja-arvon olemassaolon ja toinen taas funktion arvon ja raja-arvon yhtäsuuruuden kohdassa 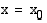. Tätä ehtoa käytetään erityisesti tutkittaessa paloittain määriteltyjen funktioiden jatkuvuutta määrittelyvälien päätepisteissä.

Edellisessä luvussa esitellyistä funktioista polynomifunktiot ovat jatkuvia koko reaalilukujen joukossa. Rationaalifunktiot ovat jatkuvia muualla paitsi nimittäjän nollakohdissa, joissa niitä ei ole määritelty. Potenssi-, juuri-, eksponentti-, logaritmi-, ja trigonometriset funktiot ovat kaikki määrittelyjoukossaan jatkuvia. Raja-arvon laskusääntöjen nojalla on helppo osoitaa, että jatkuvien funktioiden summa, erotus, tulo ja osamäärä ovat myös määrittelyjoukossaan jatkuvia. Lisäksi jatkuvista funktioista muodostettu yhdistetty funktio on määrittelyjoukossaan jatkuva.

Esimerkki 5.6.

Valtion tuloveroasteikko oli vuonna 1997 seuraavan taulukon mukainen

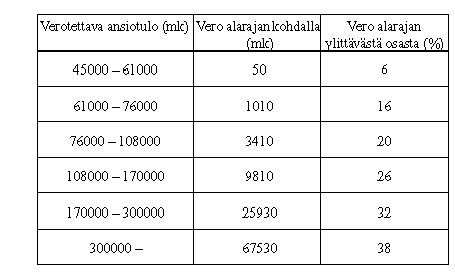
Muodosta funktio, joka ilmoittaa valtion tuloveron 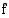(mk) verotettavan ansiotulon 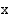(mk) funktiona. Onko tämä funktio jatkuva?

Ratkaisu:

Valtion tulovero verotettavan ansiotulon 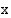(mk) funktiona on

 

Koska verofunktio on kaikilla määrittelyväleillään ensimmäisen asteen polynomifunktio, joka on kaikkialla jatkuva, sen ainoat mahdolliset epäjatkuvuuskohdat ovat määrittelyvälien päätepisteet.

Tutkitaan jatkuvuusehdon

 

voimassaolo erikseen jokaisen määrittelyvälin päätepisteessä. Oheiseen taulukkoon on laskettu verofunktion vasemman- ja oikeanpuoleiset raja-arvot sekä funktion arvo näissä pisteissä ja päätelty arvojen perusteella, onko verofunktio jatkuva ko.kohdissa.

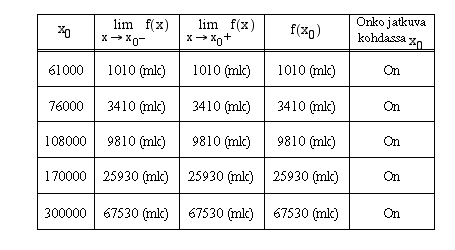
Koska funktio 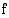on jatkuva myös määrittelyvälien päätepisteissä, se on jatkuva koko määrittelyjoukossaan.

Vastaus:   Edellä muodostettu valtion tuloverofunktio on jatkuva.

Bolzanon lause

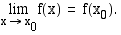
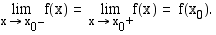
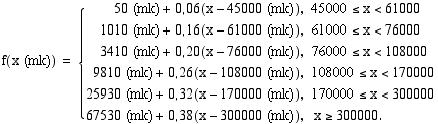
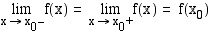
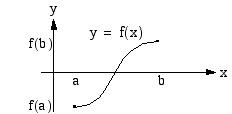Olkoon funktio 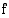jatkuva suljetulla välillä 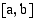. Jos arvot 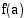ja 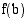ovat erimerkkiset, niin välillä 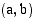on ainakin yksi kohta 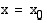, jossa 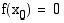. Tätä lausetta kutsutaan Bolzanon lauseeksi. Sen avulla voidaan määrittää likiarvoja funktion nollakohdille kaventamalla väliä, jolta nollakohta löytyy, halutulle tarkkuudelle.

Esimerkki 5.7.

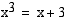Yhtälöllä on yksi reaalijuuri. Määrää sen likiarvo yhden desimaalin tarkkuudella.

Ratkaisu:

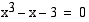Kirjoitetaan yhtälö muotoon , jolloin yhtälön ratkaisu on funktion 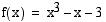nollakohta. Funktio 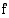on kaikkialla jatkuva. Koska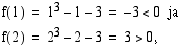

 

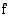funktiolla on nollakohta ja esimerkin yhtälöllä ratkaisu välillä 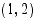. Haarukoidaan ratkaisuväliä Bolzanon lauseen avulla aina pienemmäksi ja pienemmäksi, kunnes haluttu tarkkuus saavutetaan.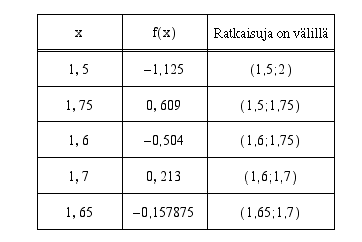

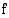Koska funktion nollakohta on välillä 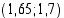, yhtälön 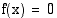ratkaisun yksidesimaalinen likiarvo on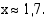

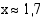
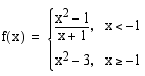
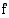Vastaus:   

Harjoituksia

5.  Onko funktio

 

jatkuva?

Vastaus tehtävään 5

6.  Äitiys-, isyys- ja vanhempainraha sekä sairauspäiväraha ja kuntoutusraha (mk/vrk) määräytyvät vuotuisten työtulojen 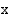(mk/v) perusteella seuraavasti (Kela 1998)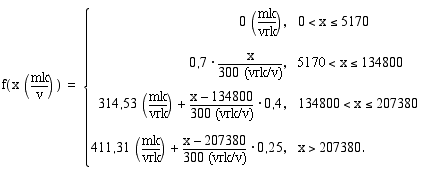

 

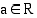Tutki, onko tämä funktio jatkuva.

Vastaus tehtävään 6

7.  Määrää vakio siten, että funktio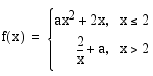

 

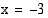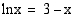on jatkuva kaikkialla. Piirrä tämän jatkuvan funktion kuvaaja.

Vastaus tehtävään 7

8.  Konstruoi koko reaalilukujen joukossa määritelty funktio, jonka ainoa epäjatkuvuuskohta on .

Vastaus tehtävään 8

9.  Osoita piirtämällä, että yhtälöllä on täsmälleen yksi ratkaisu. Määrää sen likiarvo yhden desimaalin tarkkuudella.

Vastaus tehtävään 9