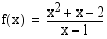
ei ole määritelty, kun 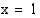 . Funktio on kuitenkin määritelty kohdan
. Funktio on kuitenkin määritelty kohdan 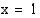 läheisyydessä. Tutki, mitä funktion
läheisyydessä. Tutki, mitä funktion 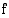 arvoille tapahtuu, kun muuttujan
arvoille tapahtuu, kun muuttujan 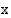 arvot lähestyvät lukua 1.
arvot lähestyvät lukua 1.
Lasketaan funktion arvoja kohdan 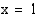 molemmin puolin.
molemmin puolin.
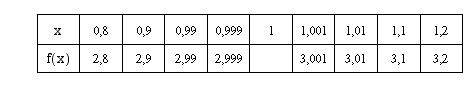
Taulukon mukaan funktion 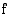 arvot lähestyvät lukua 3, kun muuttujan
arvot lähestyvät lukua 3, kun muuttujan 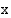 arvot lähestyvät lukua 1 sekä oikealta että vasemmalta.
arvot lähestyvät lukua 1 sekä oikealta että vasemmalta.
Vastaus: Funktion arvot lähestyvät lukua 3, kun muuttujan arvot lähestyvät lukua 1.
Sanotaan, että edellisen esimerkin funktion 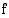 raja-arvo kohdassa
raja-arvo kohdassa 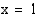 on 3. Tätä merkitään
on 3. Tätä merkitään
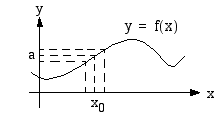 Funktiolla
Funktiolla 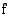 on kohdassa
on kohdassa 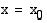 raja-arvo
raja-arvo 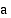 , merkitään
, merkitään
jos funktion arvot 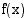 tulevat miten tahansa lähelle lukua
tulevat miten tahansa lähelle lukua 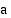 , kun muuttujan
, kun muuttujan 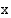 arvot ovat riittävän lähellä lukua
arvot ovat riittävän lähellä lukua 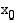 . Raja-arvo voidaan merkitä myös
. Raja-arvo voidaan merkitä myös 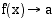 , kun
, kun 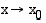 . [
Lyhenne lim tulee latinan kielen sanasta limes, joka tarkoittaa rajaa.
]
. [
Lyhenne lim tulee latinan kielen sanasta limes, joka tarkoittaa rajaa.
]
Raja-arvo kuvaa funktion käyttäytymistä tietyn kohdan läheisyydessä, ei tässä kohdassa. Jos funktion raja-arvo kohdassa 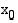 on
on 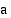 , funktio ei välttämättä ole edes määritelty tässä kohdassa. Jos funktio on määritelty, kun
, funktio ei välttämättä ole edes määritelty tässä kohdassa. Jos funktio on määritelty, kun 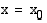 , funktion arvo
, funktion arvo 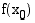 ei välttämättä ole sama kuin sen raja-arvo tässä kohdassa. Kaikissa oheisen kuvan tapauksissa funktion
ei välttämättä ole sama kuin sen raja-arvo tässä kohdassa. Kaikissa oheisen kuvan tapauksissa funktion 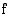 raja-arvo kohdassa
raja-arvo kohdassa 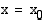 on sama, mutta keskimmäisessä tapauksessa funktio ei ole määritelty tässä kohdassa ja oikeanpuolesen kuvion funktion raja-arvo ja funktion arvo kohdassa
on sama, mutta keskimmäisessä tapauksessa funktio ei ole määritelty tässä kohdassa ja oikeanpuolesen kuvion funktion raja-arvo ja funktion arvo kohdassa 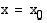 ovat erisuuret.
ovat erisuuret.
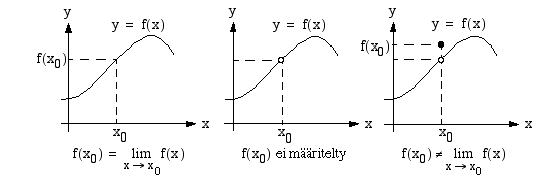
Jotta funktiolla 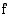 olisi raja-arvo
olisi raja-arvo 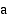 kohdassa
kohdassa 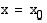 , on funktion arvojen
, on funktion arvojen 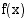 lähestyttävä lukua
lähestyttävä lukua 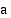 lähestyttiinpä kohtaa
lähestyttiinpä kohtaa 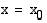 oikealta tai vasemmalta. Oheisen kuvan funktion
oikealta tai vasemmalta. Oheisen kuvan funktion 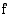 arvot lähestyvät lukua 2, kun lähestytään kohtaa
arvot lähestyvät lukua 2, kun lähestytään kohtaa 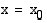 vasemmalta, ja lukua 3, kun kohtaa lähestytään oikealta.
vasemmalta, ja lukua 3, kun kohtaa lähestytään oikealta. 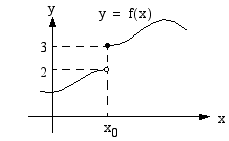 Sanotaan, että funktion
Sanotaan, että funktion 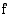 vasemmanpuoleinen raja-arvo kohdassa
vasemmanpuoleinen raja-arvo kohdassa 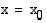 on 2, merkitään
on 2, merkitään
ja
oikeanpuoleinen raja-arvo kohdassa 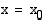 on 3, merkitään
on 3, merkitään
Funktiolla 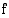 on kohdassa
on kohdassa 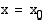 raja-arvo ainoastaan, jos nämä ns.
toispuoleiset raja-arvot ovat yhtäsuuret:
raja-arvo ainoastaan, jos nämä ns.
toispuoleiset raja-arvot ovat yhtäsuuret:
Funktiolla ei myöskään ole raja-arvoa kohdassa 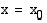 , jos funktion arvot kasvavat (tai vähenevät) rajatta lähestyttäessä tätä kohtaa sekä vasemmalta että oikealta. Esimerkiksi funktiolla
, jos funktion arvot kasvavat (tai vähenevät) rajatta lähestyttäessä tätä kohtaa sekä vasemmalta että oikealta. Esimerkiksi funktiolla 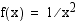 ei ole raja-arvoa kohdassa
ei ole raja-arvoa kohdassa 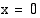 , koska
, koska 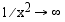 , kun
, kun 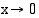 . Sanotaan, että funktiolla
. Sanotaan, että funktiolla 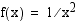 on kohdassa
on kohdassa 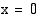 epäoleellinen raja-arvo ääretön, jota merkitään
epäoleellinen raja-arvo ääretön, jota merkitään
Funktion raja-arvo voidaan määrittää algebrallisesti seuraavien laskusääntöjen avulla.
Edellä esitettyjen laskusääntöjen nojalla polynomifunktion ja rationaalifunktion raja-arvo sen määrittelyjoukon pisteessä on sama kuin funktion arvo, jolloin raja-arvo voidaan laskea suoraan sijoittamalla.
Rationaalifunktiolla voi olla raja-arvo myös sen nimittäjän nollakohdassa, jossa funktio ei ole määritelty. Tällöin rationaalifunktion lauseke on mahdollista muokata (esim. supistamalla) muotoon, joka on määritelty ko. kohdassa.
Funktio ei ole määritelty kohdassa 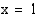 . Kun
. Kun 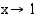 , tarkasteltavan rationaalifunktion osoittaja ja nimittäjä lähestyvät nollaa. Koska
, tarkasteltavan rationaalifunktion osoittaja ja nimittäjä lähestyvät nollaa. Koska 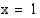 on sekä osoittajan että nimittäjän nollakohta, molemmat ovat jaollisia
on sekä osoittajan että nimittäjän nollakohta, molemmat ovat jaollisia 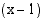 :llä. Jaetaan osoittaja ja nimittäjä tekijöihin ja supistetaan niiden yhteisellä tekijällä. Jos muodostunut lauseke on määritelty kohdassa
:llä. Jaetaan osoittaja ja nimittäjä tekijöihin ja supistetaan niiden yhteisellä tekijällä. Jos muodostunut lauseke on määritelty kohdassa 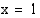 , raja-arvo on olemassa ja se on sama kuin funktion arvo.
, raja-arvo on olemassa ja se on sama kuin funktion arvo.
HUOM! Raja-arvon määrityksessä voidaan käyttää myös seuraavanlaista merkintää
Funktio ei ole määritelty, kun 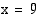 . Kun
. Kun 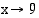 , sekä osoittaja että nimittäjä lähestyvät jälleen nollaa. Tämä viittaa siihen, että funktion lauseketta voidaan sieventää supistamalla. Lavennetaan funktion lauseke ensin erotusta
, sekä osoittaja että nimittäjä lähestyvät jälleen nollaa. Tämä viittaa siihen, että funktion lauseketta voidaan sieventää supistamalla. Lavennetaan funktion lauseke ensin erotusta 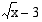 vastaavalla summalla
vastaavalla summalla 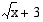 .
.
HUOM! Funktion lauseke voidaan supistaa myös ilman edellisen kaltaista lavennusta, kun huomataan, että 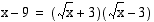 . Siis
. Siis
Määrää paraabelille 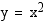 pisteeseen
pisteeseen 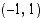 piirretyn
tangentin eli sivuajan kulmakerroin.
piirretyn
tangentin eli sivuajan kulmakerroin.
Osaamme määrittää suoran kulmakertoimen ainoastaan, jos siltä tunnetaan kaksi pistettä. Tässä tehtävässä sivuavalta suoralta kuitenkin tiedetään vain sivuamispiste 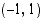 . Ratkaistaan tehtävä epäsuorasti. Paraabelin
sekantti on suora, joka leikkaa käyrän kahdessa eri pisteessä. Määrätään pisteen
. Ratkaistaan tehtävä epäsuorasti. Paraabelin
sekantti on suora, joka leikkaa käyrän kahdessa eri pisteessä. Määrätään pisteen 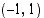 kautta kulkevan sekantin kulmakerroin. Kun toinen leikkauspiste lähestyy pistettä
kautta kulkevan sekantin kulmakerroin. Kun toinen leikkauspiste lähestyy pistettä 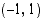 , sekantti lähestyy tähän pisteeseen piirrettyä tangenttia. Kyseisen tangentin kulmakerroin saadaankin sekantin kulmakertoimen raja-arvona.
, sekantti lähestyy tähän pisteeseen piirrettyä tangenttia. Kyseisen tangentin kulmakerroin saadaankin sekantin kulmakertoimen raja-arvona.
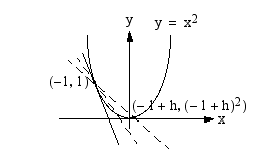
Olkoon pisteen 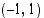 kautta kulkevan sekantin ja paraabelin toinen leikkauspiste
kautta kulkevan sekantin ja paraabelin toinen leikkauspiste 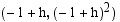 . Sekantin kulmakerroin on tällöin
. Sekantin kulmakerroin on tällöin
Toinen leikkauspiste lähestyy pistettä 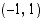 ja sekantti kiertyy tangentin suuntaiseksi, kun
ja sekantti kiertyy tangentin suuntaiseksi, kun 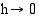 . Paraabelille
. Paraabelille 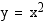 pisteeseen
pisteeseen 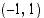 piirretyn tangetin kulmakerroin on siten raja-arvo
piirretyn tangetin kulmakerroin on siten raja-arvo