3.6. Ellipsi
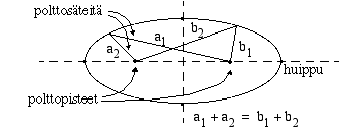 Ellipsi on niiden tason pisteiden joukko, joiden kahdesta kiinteästä pisteestä mitattujen etäisyyksien summa on vakio. Nämä pisteet ovat ellipsin
polttopisteet. Ellipsiltä polttopisteisiin piirrettyjä etäisyysjanoja sanotaan
polttosäteiksi. Ellipsi voidaan piirtää käyttämällä apuna polttosäteiden summan mittaista lankaa, jonka päät on kiinnitetty polttopisteisiin. Ellipsi on symmetrinen sekä polttopisteiden kautta kulkevan suoran että polttopisteiden välisen janan keskinormaalin suhteen. Ellipsin ja sen symmetria-akselien leikkauspisteitä kutsutaan ellipsin
huipuiksi.
Ellipsi on niiden tason pisteiden joukko, joiden kahdesta kiinteästä pisteestä mitattujen etäisyyksien summa on vakio. Nämä pisteet ovat ellipsin
polttopisteet. Ellipsiltä polttopisteisiin piirrettyjä etäisyysjanoja sanotaan
polttosäteiksi. Ellipsi voidaan piirtää käyttämällä apuna polttosäteiden summan mittaista lankaa, jonka päät on kiinnitetty polttopisteisiin. Ellipsi on symmetrinen sekä polttopisteiden kautta kulkevan suoran että polttopisteiden välisen janan keskinormaalin suhteen. Ellipsin ja sen symmetria-akselien leikkauspisteitä kutsutaan ellipsin
huipuiksi.
Tällä kurssilla tarkastellaan ainoastaan ellipsejä, joiden keskipiste on origo ja huiput koordinaattiakseleilla. Ellipsillä, jonka huiput ovat pisteissä 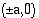 ja
ja 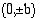 on yhtälö
on yhtälö
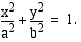
Janat 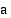 ja
ja 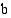 ovat ellipsin
puoliakseleita.
ovat ellipsin
puoliakseleita.
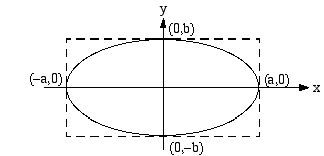 Tämä ellipsi voidaan piirtää oheisen kuvion mukaisesti käyttämällä apukuviona suorakulmiota, jonka sivut ovat koordinaattiakselien suuntaiset ja joka leikkaa koordinaattiakselit ellipsin huippupisteissä. Halutessaan tarkemman kuvion voi lisäksi laskea ellipsiltä joitakin pisteitä.
Tämä ellipsi voidaan piirtää oheisen kuvion mukaisesti käyttämällä apukuviona suorakulmiota, jonka sivut ovat koordinaattiakselien suuntaiset ja joka leikkaa koordinaattiakselit ellipsin huippupisteissä. Halutessaan tarkemman kuvion voi lisäksi laskea ellipsiltä joitakin pisteitä.
Esimerkki 3.13.
Määrää ellipsin 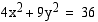 huiput.
huiput.
Ratkaisu:
Muutetaan ellipsin yhtälö puoliakselimuotoon.
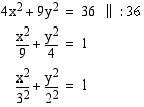
Vastaus: Ellipsin huiput ovat 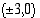 ja
ja 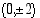 .
.
Ellipsin tunsivat jo antiikin matemaaatikot. Esimerkiksi planeettojen radat ovat ellipsejä, joiden polttopisteenä on Auringon keskipiste, ja Kuun rata on ellipsi, jonka toisena polttopisteenä on Maan keskipiste.
Esimerkki 3.14.
Maan lyhin etäisyys Auringosta on 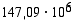 (km) ja pisin etäisyys
(km) ja pisin etäisyys 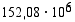 (km). Mitkä ovat Maan radan puoliakselien pituudet?
(km). Mitkä ovat Maan radan puoliakselien pituudet?
Ratkaisu:
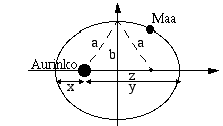 Sijoitetaan Maan rata koordinaatistoon, jonka origo on ellipsiradan keskipisteessä. Tällöin ellipsin poltto-pisteet, joista toinen on Auringon keskipiste, ovat koordinaattiakselilla. Olkoon Maan lyhin etäisyys Auringosta
Sijoitetaan Maan rata koordinaatistoon, jonka origo on ellipsiradan keskipisteessä. Tällöin ellipsin poltto-pisteet, joista toinen on Auringon keskipiste, ovat koordinaattiakselilla. Olkoon Maan lyhin etäisyys Auringosta 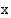 ja pisin
ja pisin 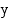 , ja olkoot Maan radan puoliakselit
, ja olkoot Maan radan puoliakselit 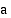 ja
ja 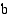 (
(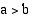 ).
).
Osoitetaan ensin, että ellipsiradalta sen polttopisteisiin piirrettyjen polttosäteiden summa on 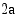 . Määritelmän mukaan tämä polttosäteiden summa on vakio. Kun Maan etäisyys Auringosta on pisimmillään (tai lyhimmillään), Maasta radan polttopisteisiin piirrettyjen polttosäteiden summa on oheisen kuvion merkinnöin
. Määritelmän mukaan tämä polttosäteiden summa on vakio. Kun Maan etäisyys Auringosta on pisimmillään (tai lyhimmillään), Maasta radan polttopisteisiin piirrettyjen polttosäteiden summa on oheisen kuvion merkinnöin 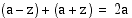 .
.
Toisaalta polttosäteiden summa on tässä 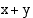 . Merkitään nämä yhtäsuuriksi ja ratkaistaan pisempi puoliakseli saadusta yhtälöstä.
. Merkitään nämä yhtäsuuriksi ja ratkaistaan pisempi puoliakseli saadusta yhtälöstä.
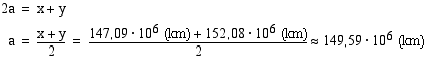
Kun Maa sijaitsee radan huipussa toisella koordinaattiakselilla, sen etäisyys kummastakin radan polttopisteestä on symmetrian nojalla sama. Koska etäisyyksien summa on 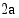 , on kummankin etäisyyden oltava
, on kummankin etäisyyden oltava 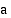 . Kuvioon muodostuu suorakulmainen kolmio, jonka hypotenuusa on
. Kuvioon muodostuu suorakulmainen kolmio, jonka hypotenuusa on 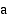 ja pisempi kateetti radan toinen puoliakseli
ja pisempi kateetti radan toinen puoliakseli 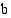 ja lyhyempi kateetti kuvion merkinnöin
ja lyhyempi kateetti kuvion merkinnöin 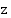 .
.
Ratkaistaan ensin 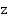 . Koska
. Koska 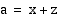 , on
, on 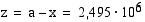 (km). Puuttuva radan puoliakseli voidaan nyt ratkaista Pythagoraan lauseen avulla.
(km). Puuttuva radan puoliakseli voidaan nyt ratkaista Pythagoraan lauseen avulla.
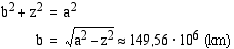
Vastaus: Radan puoliakselit ovat 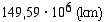 ja
ja 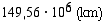 .
.
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
 Ellipsi on niiden tason pisteiden joukko, joiden kahdesta kiinteästä pisteestä mitattujen etäisyyksien summa on vakio. Nämä pisteet ovat ellipsin
polttopisteet. Ellipsiltä polttopisteisiin piirrettyjä etäisyysjanoja sanotaan
polttosäteiksi. Ellipsi voidaan piirtää käyttämällä apuna polttosäteiden summan mittaista lankaa, jonka päät on kiinnitetty polttopisteisiin. Ellipsi on symmetrinen sekä polttopisteiden kautta kulkevan suoran että polttopisteiden välisen janan keskinormaalin suhteen. Ellipsin ja sen symmetria-akselien leikkauspisteitä kutsutaan ellipsin
huipuiksi.
Ellipsi on niiden tason pisteiden joukko, joiden kahdesta kiinteästä pisteestä mitattujen etäisyyksien summa on vakio. Nämä pisteet ovat ellipsin
polttopisteet. Ellipsiltä polttopisteisiin piirrettyjä etäisyysjanoja sanotaan
polttosäteiksi. Ellipsi voidaan piirtää käyttämällä apuna polttosäteiden summan mittaista lankaa, jonka päät on kiinnitetty polttopisteisiin. Ellipsi on symmetrinen sekä polttopisteiden kautta kulkevan suoran että polttopisteiden välisen janan keskinormaalin suhteen. Ellipsin ja sen symmetria-akselien leikkauspisteitä kutsutaan ellipsin
huipuiksi.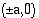 ja
ja 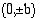 on yhtälö
on yhtälö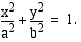
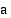 ja
ja 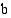 ovat ellipsin
puoliakseleita
ovat ellipsin
puoliakseleita Tämä ellipsi voidaan piirtää oheisen kuvion mukaisesti käyttämällä apukuviona suorakulmiota, jonka sivut ovat koordinaattiakselien suuntaiset ja joka leikkaa koordinaattiakselit ellipsin huippupisteissä. Halutessaan tarkemman kuvion voi lisäksi laskea ellipsiltä joitakin pisteitä.
Tämä ellipsi voidaan piirtää oheisen kuvion mukaisesti käyttämällä apukuviona suorakulmiota, jonka sivut ovat koordinaattiakselien suuntaiset ja joka leikkaa koordinaattiakselit ellipsin huippupisteissä. Halutessaan tarkemman kuvion voi lisäksi laskea ellipsiltä joitakin pisteitä.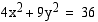 huiput.
huiput.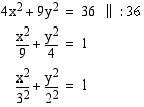
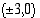 ja
ja 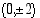 .
.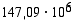 (km) ja pisin etäisyys
(km) ja pisin etäisyys 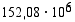 (km). Mitkä ovat Maan radan puoliakselien pituudet?
(km). Mitkä ovat Maan radan puoliakselien pituudet? Sijoitetaan Maan rata koordinaatistoon, jonka origo on ellipsiradan keskipisteessä. Tällöin ellipsin poltto-pisteet, joista toinen on Auringon keskipiste, ovat koordinaattiakselilla. Olkoon Maan lyhin etäisyys Auringosta
Sijoitetaan Maan rata koordinaatistoon, jonka origo on ellipsiradan keskipisteessä. Tällöin ellipsin poltto-pisteet, joista toinen on Auringon keskipiste, ovat koordinaattiakselilla. Olkoon Maan lyhin etäisyys Auringosta 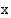 ja pisin
ja pisin 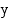 , ja olkoot Maan radan puoliakselit
, ja olkoot Maan radan puoliakselit 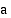 ja
ja 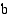 (
(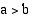 ).
). 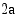 . Määritelmän mukaan tämä polttosäteiden summa on vakio. Kun Maan etäisyys Auringosta on pisimmillään (tai lyhimmillään), Maasta radan polttopisteisiin piirrettyjen polttosäteiden summa on oheisen kuvion merkinnöin
. Määritelmän mukaan tämä polttosäteiden summa on vakio. Kun Maan etäisyys Auringosta on pisimmillään (tai lyhimmillään), Maasta radan polttopisteisiin piirrettyjen polttosäteiden summa on oheisen kuvion merkinnöin 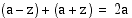 .
. 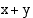 . Merkitään nämä yhtäsuuriksi ja ratkaistaan pisempi puoliakseli saadusta yhtälöstä.
. Merkitään nämä yhtäsuuriksi ja ratkaistaan pisempi puoliakseli saadusta yhtälöstä.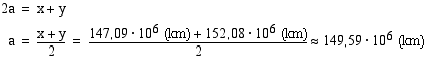
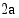 , on kummankin etäisyyden oltava
, on kummankin etäisyyden oltava 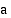 . Kuvioon muodostuu suorakulmainen kolmio, jonka hypotenuusa on
. Kuvioon muodostuu suorakulmainen kolmio, jonka hypotenuusa on 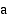 ja pisempi kateetti radan toinen puoliakseli
ja pisempi kateetti radan toinen puoliakseli 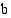 ja lyhyempi kateetti kuvion merkinnöin
ja lyhyempi kateetti kuvion merkinnöin 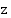 .
. 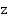 . Koska
. Koska 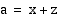 , on
, on 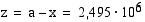 (km). Puuttuva radan puoliakseli voidaan nyt ratkaista Pythagoraan lauseen avulla.
(km). Puuttuva radan puoliakseli voidaan nyt ratkaista Pythagoraan lauseen avulla.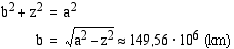
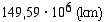 ja
ja 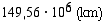 .
.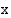 - ja
- ja 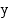 -akseleilla olevat puoliakselit ovat
-akseleilla olevat puoliakselit ovat 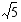 ja 3.
ja 3.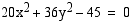 .
.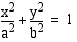
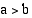 .
.