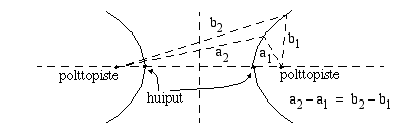
Hyperbeli on niiden tason pisteiden joukko, joiden kahdesta kiinteästä pisteestä mitattujen etäisyyksien erotus on vakio. Näitä pisteitä nimitetään hyperbelin polttopisteiksi. Hyperbeli on symmetrinen polttopisteiden kautta kulkevan suoran ja polttopisteiden välisen janan keskinormaalin suhteen. Hyperbelin ja sen symmetria-akselin leikkauspisteet ovat hyperbelin huiput.

Tällä kurssilla rajoitutaan kolmeen erikoistapaukseen hyperbeleistä.
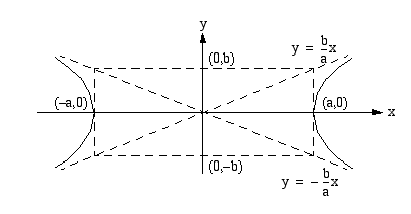
Kun hyperbelin polttopisteet sijaitsevat 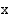 -akselilla symmetrisesti origon suhteen, sen yhtälö on
-akselilla symmetrisesti origon suhteen, sen yhtälö on
Hyperbeli leikkaa 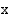 -akselin huippupisteissä
-akselin huippupisteissä 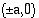 ja sen puoliakselit ovat
ja sen puoliakselit ovat 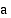 ja
ja 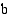 . Kun
. Kun 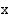 :n itseisarvo kasvaa, hyperbeli lähestyy rajatta suoria
:n itseisarvo kasvaa, hyperbeli lähestyy rajatta suoria 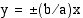 , joita kutsutaan hyperbelin
asymptooteiksi.
, joita kutsutaan hyperbelin
asymptooteiksi.
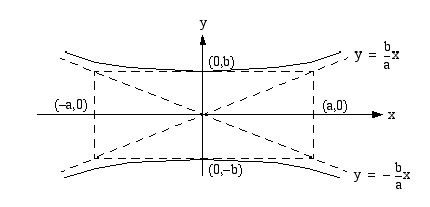
Tämän hyperbelin piirtämiseksi kannattaa tehdä oheisen kuvan kaltainen apukuvio. Se koostuu pisteiden 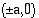 ja
ja 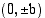 kautta kulkevasta suorakulmiosta, jonka sivut ovat koordinaattiakselien suuntaiset sekä tämän suorakulmion lävistäjäsuorista. Nämä lävistäjät ovat hyperbelin
kautta kulkevasta suorakulmiosta, jonka sivut ovat koordinaattiakselien suuntaiset sekä tämän suorakulmion lävistäjäsuorista. Nämä lävistäjät ovat hyperbelin
asymptootit. Hyperbeli hahmotellaan kuvan osoittamalla tavalla huipuista lähestymään asymptoottisesti suorakulmion lävistäjäsuoria.
Toinen erikoistapaus on edellä esitellyn hyperbelin ns. liittohyperbeli. Sen yhtälö on
Tämän hyperbelin huiput ovat 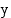 -akselilla pisteissä
-akselilla pisteissä 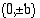 ja myös sen asymptootteina ovat suorat
ja myös sen asymptootteina ovat suorat 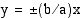 .
.
Yhtälö 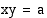 , missä
, missä 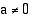 , esittää hyperbeliä, jonka asymptootteina ovat koordinaattiakselit. Tämä havaitaan, kun esitetään yhtälö muodossa
, esittää hyperbeliä, jonka asymptootteina ovat koordinaattiakselit. Tämä havaitaan, kun esitetään yhtälö muodossa 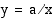 . Kun
. Kun 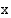 :n arvot kasvavat itseisarvoltaan rajatta, osamäärä lähestyy nollaa ja kuvaaja
:n arvot kasvavat itseisarvoltaan rajatta, osamäärä lähestyy nollaa ja kuvaaja 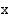 -akselia. Kun
-akselia. Kun 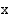 :n arvot lähestyvät nollaa, osamäärä joko kasvaa tai vähenee rajatta ja kuvaaja lähestyy
:n arvot lähestyvät nollaa, osamäärä joko kasvaa tai vähenee rajatta ja kuvaaja lähestyy 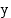 -akselia. Hyperbelin
-akselia. Hyperbelin 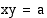 , missä
, missä 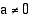 , huiput ovat
, huiput ovat
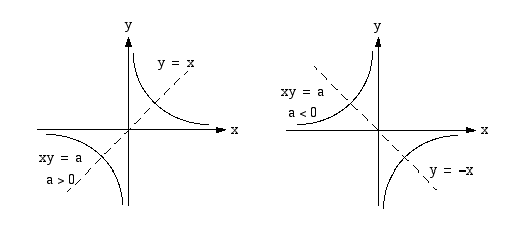
Määrää seuraavien hyperbelien huiput ja asymptootit.
(a) Muutetaan hyperbelin yhtälö ensin puoliakselimuotoon.
Hyperbelin huiput ovat pisteissä 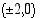 ja sen asymptootit ovat
ja sen asymptootit ovat
(b) Tämäkin yhtälö on ensin muutettava puoliakselimuotoon.
Hyperbelin huiput ovat pisteissä 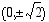 ja sen asymptootit ovat
ja sen asymptootit ovat
(c) Hyperbelin huiput ovat suoralla 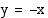 . Määrätään huiput ratkaisemalla yhtälöpari
. Määrätään huiput ratkaisemalla yhtälöpari
Yhtälöparin ratkaisut ovat 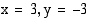 ja
ja 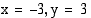 . Hyperbelin asymptootteina ovat koordinaattiakselit.
. Hyperbelin asymptootteina ovat koordinaattiakselit.
38. Määrää hyperbelin 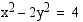 huiput ja asymptootit.
huiput ja asymptootit.
39. Hyperbelin huiput ovat pisteissä 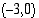 ja
ja 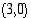 . Määrää hyperbelin yhtälö, kun sen toisena asymptoottina on suora
. Määrää hyperbelin yhtälö, kun sen toisena asymptoottina on suora 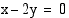 .
.
40. Määrää graafisesti käyrien 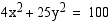 ja
ja 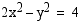 leikkauspisteet.
leikkauspisteet.
41. Yritys myy tuotetta, jonka yksikköhinta on 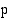 (mk/kpl). Olkoon vuorokaudessa myyty tuotemäärä
(mk/kpl). Olkoon vuorokaudessa myyty tuotemäärä 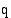 (kpl/vrk). Tällöin yrityksen myyntitulot
(kpl/vrk). Tällöin yrityksen myyntitulot 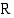 (mk/vrk) ovat
(mk/vrk) ovat 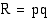 . Oletetaan, että yrityksen myyntitulot pysyvät vakiona:
. Oletetaan, että yrityksen myyntitulot pysyvät vakiona: 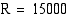 (mk/vrk). Esitä vakiona säilyvät myyntitulot hyperbelinä
(mk/vrk). Esitä vakiona säilyvät myyntitulot hyperbelinä 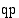 -koordinaatistossa ja tulkitse kuvaajan pisteet.
-koordinaatistossa ja tulkitse kuvaajan pisteet.