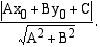3.4. Ympyrä
Ympyrä on niiden tason pisteiden joukko, jotka ovat säteen etäisyydellä ympyrän keskipisteestä.
Olkoon ympyrän keskipiste 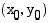 ja säde
ja säde 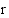 . Johdetaan ympyrän yhtälö.
. Johdetaan ympyrän yhtälö. 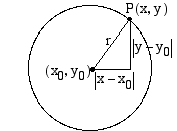 Piste
Piste 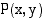 on ympyrän kehällä, jos sen etäisyys keskipisteestä
on ympyrän kehällä, jos sen etäisyys keskipisteestä 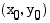 on säde
on säde 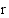 . Tämä etäisyysjana on hypotenuusana oheisessa suorakulmaisessa kolmiossa, jonka kateettien pituudet ovat
. Tämä etäisyysjana on hypotenuusana oheisessa suorakulmaisessa kolmiossa, jonka kateettien pituudet ovat 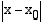 ja
ja 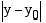 . Pythagoraan lauseen nojalla on oltava voimassa
. Pythagoraan lauseen nojalla on oltava voimassa
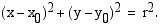
Tämä on 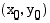 -keskisen
-keskisen 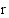 -säteisen ympyrän yhtälö. Edellä esitetty yhtälö on ympyrän yhtälön
keskipistemuoto. Suorittamalla potenssiinkorotukset ympyrän yhtälö saadaan ns.
yleiseen muotoon.
-säteisen ympyrän yhtälö. Edellä esitetty yhtälö on ympyrän yhtälön
keskipistemuoto. Suorittamalla potenssiinkorotukset ympyrän yhtälö saadaan ns.
yleiseen muotoon.
Huom!
Origokeskisen ympyrän yhtälö on
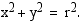
Esimerkki 3.10.
Tarkastellaan ympyrää 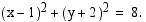
(a) Mikä on ympyrän keskipiste ja säde?
(b) Mikä on ympyrän yhtälön yleinen muoto?
(c) Onko piste 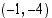 ympyrän kehällä?
ympyrän kehällä?
(d) Missä pisteissä suora 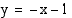 leikkaa ympyrän kehän?
leikkaa ympyrän kehän?
Ratkaisu:
(a) Ympyrän keskipiste on 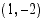 ja säde
ja säde 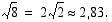
(b) Suoritetaan yhtälön potenssiinkorotukset.
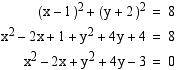
(c) Piste 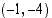 on ympyrän kehällä, jos se toteuttaa ympyrän yhtälön. Sijoitetaan pisteen koordinaatit ympyrän yhtälöön.
on ympyrän kehällä, jos se toteuttaa ympyrän yhtälön. Sijoitetaan pisteen koordinaatit ympyrän yhtälöön.
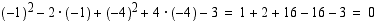
Koska pisteen koordinaatit toteuttavat ympyrän yhtälön, piste on sen kehällä.
(d) Suoran ja ympyrän leikkauspiste saadaan ratkaisemalla yhtälöpari
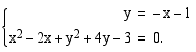
Käytetään sijoituskeinoa.
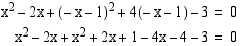
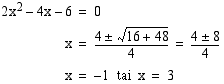
Lasketaan lopuksi leikkauspisteiden 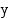 -koordinaatit. Kun
-koordinaatit. Kun 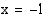 , niin
, niin 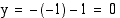 , ja kun
, ja kun 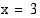 , niin
, niin 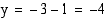 .
.
Vastaus: (a) Keskipiste on 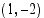 ja säde
ja säde 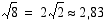 .
.
(b) Ympyrän yhtälön yleinen muoto on 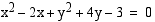 .
.
(c) On.
(d) Ympyrän ja suoran leikkauspisteet ovat 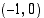 ja
ja 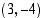 .
.
Kun suoralla ja ympyrällä on kaksi yhteistä pistettä, sanotaan suoran olevan ympyrän
sekantti. Jos suoralla ja ympyrällä on yksi yhteinen piste, suora on ympyrän
tangentti. Tangentti on kohtisuorassa sivuamispisteeseen piirrettyä sädettä vastaan. Tangentin etäisyys ympyrän keskipisteestä on säteen suuruinen.
Esimerkki 3.11.
Määrää ympyrän 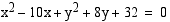 keskipiste ja säde.
keskipiste ja säde.
Ratkaisu:
Muutetaan ympyrän yhtälön yleinen muoto keskipistemuotoon täydentämällä se neliöksi.
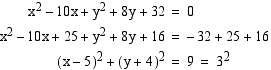
Vastaus: Keskipiste 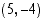 ja säde 3.
ja säde 3.
Harjoituksia
23. Muodosta yhtälö ympyrälle, jonka keskipiste on 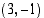 ja säde 5. Kirjoita yhtälö sekä keskipiste- että yleisessä muodossa.
ja säde 5. Kirjoita yhtälö sekä keskipiste- että yleisessä muodossa.
Vastaus tehtävään 23
24. Piirrä ympyrät 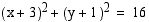 ja
ja 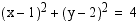 ja määrää niiden leikkauspisteet graafisesti.
ja määrää niiden leikkauspisteet graafisesti.
Vastaus tehtävään 24
25. Missä pisteissä suora 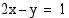 leikkaa ympyrän
leikkaa ympyrän 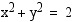 . Piirrä kuva.
. Piirrä kuva.
Vastaus tehtävään 25
26. Osoita, että ympyröiden 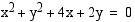 ja
ja 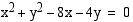 keskipisteiden välimatka on yhtä suuri kuin ympyröiden säteiden summa.
keskipisteiden välimatka on yhtä suuri kuin ympyröiden säteiden summa.
Vastaus tehtävään 26
27. Määrää sen ympyrän yhtälö, jonka keskipiste on 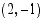 ja jonka eräs tangenttisuora on
ja jonka eräs tangenttisuora on 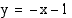 . Vihje: Käytä tietoa: suoran
. Vihje: Käytä tietoa: suoran 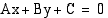 etäisyys pisteestä
etäisyys pisteestä 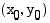 on
on
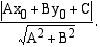
Vastaus tehtävään 27
28. Seismologiset asemat pystyvät määrittämään maanjäristyksen keskuksen etäisyyden asemasta. Maanjäristys havaittiin kahdelta eri asemalta A ja B. Keskus sijaitsi 200 (km):n päässä asemasta A ja 300 (km):n päässä asemasta B. Asemalle B päästään kulkemalla asemalta A 300 (km) länteen ja 200 (km) etelään. Missä kohdissa järistyksen keskus voi sijaita asemasta A katsottuna?
Vastaus tehtävään 28
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
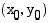 ja säde
ja säde 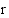 . Johdetaan ympyrän yhtälö.
. Johdetaan ympyrän yhtälö. 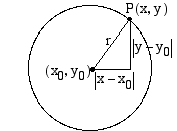 Piste
Piste 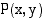 on ympyrän kehällä, jos sen etäisyys keskipisteestä
on ympyrän kehällä, jos sen etäisyys keskipisteestä 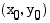 on säde
on säde 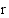 . Tämä etäisyysjana on hypotenuusana oheisessa suorakulmaisessa kolmiossa, jonka kateettien pituudet ovat
. Tämä etäisyysjana on hypotenuusana oheisessa suorakulmaisessa kolmiossa, jonka kateettien pituudet ovat 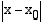 ja
ja 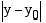 . Pythagoraan lauseen nojalla on oltava voimassa
. Pythagoraan lauseen nojalla on oltava voimassa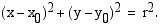
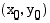 -keskisen
-keskisen 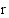 -säteisen ympyrän yhtälö. Edellä esitetty yhtälö on ympyrän yhtälön
keskipistemuoto. Suorittamalla potenssiinkorotukset ympyrän yhtälö saadaan ns.
yleiseen muotoon.
-säteisen ympyrän yhtälö. Edellä esitetty yhtälö on ympyrän yhtälön
keskipistemuoto. Suorittamalla potenssiinkorotukset ympyrän yhtälö saadaan ns.
yleiseen muotoon.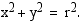
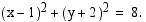
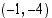 ympyrän kehällä?
ympyrän kehällä?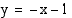 leikkaa ympyrän kehän?
leikkaa ympyrän kehän?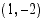 ja säde
ja säde 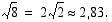
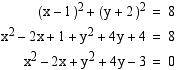
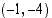 on ympyrän kehällä, jos se toteuttaa ympyrän yhtälön. Sijoitetaan pisteen koordinaatit ympyrän yhtälöön.
on ympyrän kehällä, jos se toteuttaa ympyrän yhtälön. Sijoitetaan pisteen koordinaatit ympyrän yhtälöön.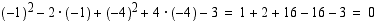
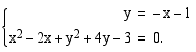
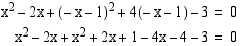
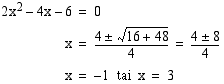
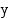 -koordinaatit. Kun
-koordinaatit. Kun 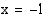 , niin
, niin 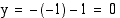 , ja kun
, ja kun 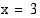 , niin
, niin 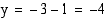 .
.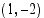 ja säde
ja säde 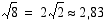 .
.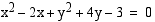 .
.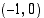 ja
ja 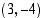 .
.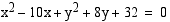 keskipiste ja säde.
keskipiste ja säde. 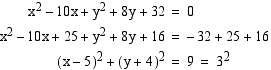
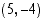 ja säde 3.
ja säde 3.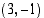 ja säde 5. Kirjoita yhtälö sekä keskipiste- että yleisessä muodossa.
ja säde 5. Kirjoita yhtälö sekä keskipiste- että yleisessä muodossa.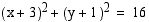 ja
ja 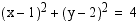 ja määrää niiden leikkauspisteet graafisesti.
ja määrää niiden leikkauspisteet graafisesti. 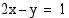 leikkaa ympyrän
leikkaa ympyrän 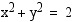 . Piirrä kuva.
. Piirrä kuva.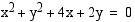 ja
ja 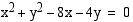 keskipisteiden välimatka on yhtä suuri kuin ympyröiden säteiden summa.
keskipisteiden välimatka on yhtä suuri kuin ympyröiden säteiden summa.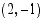 ja jonka eräs tangenttisuora on
ja jonka eräs tangenttisuora on 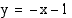 . Vihje: Käytä tietoa: suoran
. Vihje: Käytä tietoa: suoran 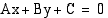 etäisyys pisteestä
etäisyys pisteestä 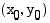 on
on