1.5. Mittayksiköllisten suureiden laskutoimitukset

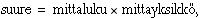
Koska tässä monisteessa kaikki suureet esitetään mittayksiköllisinä, on syytä tarkastella lähemmin mittayksiköllisten suureiden laskutoimituksia. Määritelmän mukaan

joten mittayksikkö on oleellinen osa suureen arvoa. Kuitenkin mittayksiköt on useimmiten jätetty pois erityisesti talousmatematiikan oppikirjoista. Esimerkiksi yrityksen kuukausittaisten kustannusten 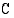riippuvuus tuotantonopeudesta 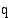on tavallisesti esitetty muodossa 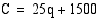, jolloin lukija ajattelee funktion määrittelyssä esiintyvien vakioiden olevan reaalilukuja, vaikka ne ovatkin mittayksiköllisiä suureita. Riippuvuussuhteen oikea esitystapa on

Tämä esitystapa auttaa myös tulkitsemaan funktion määrittelyssä esiintyvät vakiot oikein. Tässä monisteessa mittayksiköt esitetään selvyyden vuoksi aina suluissa.

Suureiden yhteenlasku on mahdollinen ainoastaan samandimensionaalisten suureiden kesken, esimerkiksi 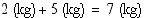. Tämä ominaisuus itse asiassa määrittelee dimensiokäsitteen: dimensio on yhteenlaskettavien suureiden joukko. Käytetään esimerkiksi ajan dimensiolle merkintää 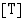, jolloin 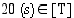, 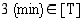ja 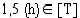, sillä

Dimensiot jaetaan perusdimensioihin ja näistä johdettuihin dimensioihin. Perusdimensiot ovat toisistaan riippumattomia yhteenlaskettavien suureiden joukkoja. Fysiikan mittajärjestelmän perusdimensioita ovat esimerkiksi 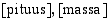ja 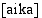. Kansantalouden perusdimensioita ovat mm. määrän dimensio 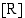"real dimension" ja arvon dimensio 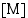"monetary dimension". Perusdimensioista voidaan muodostaa johdettuja dimensioita, jotka ovat perusdimensioiden potenssituloja ts. ne on muodostettu perusdimensioista joko kerto- tai jakolaskun avulla. Johdettuja dimensioita ovat esimerkiksi fysiikassa 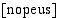, joka on , ja taloustieteessä tuotantonopeuden dimensio 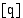, joka on 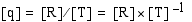. Fysiikan mittajärjestelmä on esitetty kirjassa H. C. Ohanian: Physics, Second Edition Expanded (1988). Taloustieteen mittajärjestelmää voi opiskella tarkemmin teoksista M. Estola: Kansantaloustieteen perusteet (1996) tai F. de Jong: Dimensional Analysis for Economists (1967).

Seuraavassa luettelossa on esimerkkejä mittayksiköllisten suureiden laskutoimituksista.

Edellä esitetyt yhtälöt ovat dimensiohomogeenisia eli yhtälöiden kummatkin puolet kuuluvat samaan dimensioon. Tämä vaatimus yhtälöiden on aina toteutettava. Käytännön ongelmista muodostetut yhtälöt pitäisi kirjoittaa mittayksiköineen, sillä yksiköitä voidaan käyttää apuna yhtälön oikeellisuuden takistamiseen: jos kirjoitettu yhtälö ei ole dimensiohomogeeninen, se ei voi olla oikein. Yhtälö saadaan mittayksiköttömäksi ratkaisuvaiheita varten kertomalla se puolittain sopivalla nollasta eroavalla suureella esimerkiksi näin:

Kertojana olevan suureen mittaluku on usein 1. Tämä ei kuitenkaan ole välttämätöntä. Edellinen yhtälö saadaan mittayksiköttömäksi ja yksinkertaisempaan muotoon kertomalla seuraavasti:

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]