6.3.3. Määrätyn integraalin ominaisuuksia
Määrätylle integraalille on voimassa seuraavat ominaisuudet.
Vakiolla kerrotun funktion määrätty integraali
Integroitavan funktion vakiokerroin voidaan siirtää määrätyn integraalin kertoimeksi:
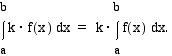
Tämä ominaisuus voidaan todistaa samoin kuin edellinenkin, joten se jätetään lukijalle harjoitustehtäväksi.
Esimerkki 6.20.
Laske määrätty integraali
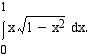
Ratkaisu:
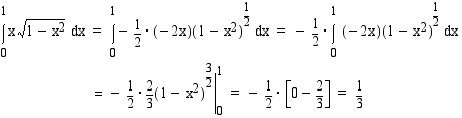
Vastaus: 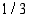
Integroimisrajat yhtä suuret
Jos määrätyn integraalin ylä- ja alaraja ovat yhtä suuret, määrätyn integraalin arvo on 0:
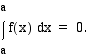
Olkoon 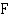 jokin funktion
jokin funktion 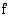 integraalifunktio. Tällöin
integraalifunktio. Tällöin
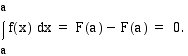
Integroimisrajojen vaihto
Jos ylä- ja alaraja vaihdetaan keskenään, määrätty integraali muuttuu vastaluvukseen:
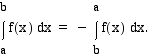
Olkoon jälleen funktio 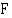 funktion
funktion 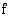 jokin integraalifunktio. Tällöin
jokin integraalifunktio. Tällöin
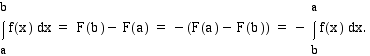
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
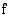 ja
ja 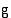 summan
summan 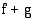 määrätty integraali on yhteenlaskettavien funktioiden määrättyjen integraalien summa:
määrätty integraali on yhteenlaskettavien funktioiden määrättyjen integraalien summa: 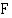 jokin funktion
jokin funktion 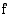 integraalifunktio ja
integraalifunktio ja 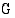 jokin funktion
jokin funktion 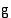 integraalifunktio, jolloin
integraalifunktio, jolloin 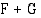 on summafunktion
on summafunktion 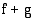 integraalifunktio. Tällöin
integraalifunktio. Tällöin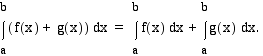
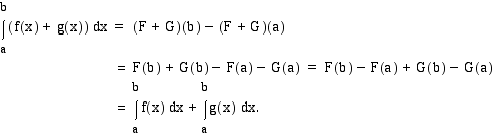
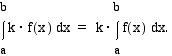
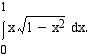
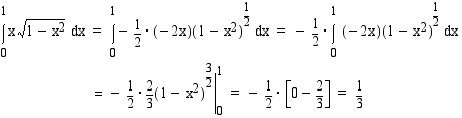
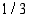
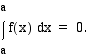
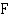 jokin funktion
jokin funktion 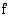 integraalifunktio. Tällöin
integraalifunktio. Tällöin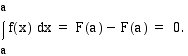
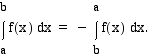
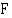 funktion
funktion 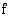 jokin integraalifunktio. Tällöin
jokin integraalifunktio. Tällöin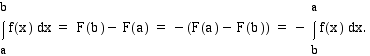
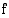 määrätyt integraalit
määrätyt integraalit 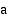 :sta
:sta 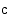 :hen ja
:hen ja 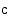 :stä
:stä 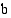 :hen, summa on yhtä suuri kuin funktion
:hen, summa on yhtä suuri kuin funktion 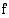 määrätty integraali
määrätty integraali 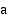 :sta
:sta 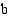 :hen:
:hen: 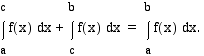
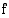 on jatkuva välillä, joka sisältää luvut
on jatkuva välillä, joka sisältää luvut 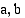 ja
ja 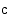 . Luvun
. Luvun 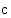 ei tarvitse kuulua välille
ei tarvitse kuulua välille 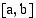 .
.