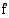 on jatkuva välillä
on jatkuva välillä 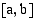 , niin määrätty integraali
, niin määrätty integraali
Jos funktio 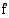 on jatkuva välillä
on jatkuva välillä 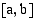 , niin määrätty integraali
, niin määrätty integraali
missä 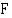 on jokin funktion
on jokin funktion 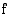 integraalifunktio.
integraalifunktio.
Perustelu: Muodostetaan pinta-alafunktio 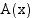 , joka ilmoittaa välillä
, joka ilmoittaa välillä 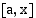 funktion
funktion 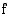 kuvaajan ja
kuvaajan ja 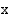 -akselin väliin jäävän alueen pinta-alan. Tällöin
-akselin väliin jäävän alueen pinta-alan. Tällöin 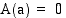 ja
ja
Osoitetaan ensin, että pinta-alafunktion 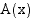 derivaatta
derivaatta 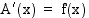 . Funktion
. Funktion 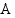 erotusosamäärä kohdassa
erotusosamäärä kohdassa 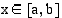 on
on
Erotusosamäärän osoittaja 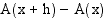 on käyrän
on käyrän 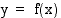 ja
ja 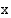 -akselin välillä
-akselin välillä 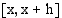 rajoittaman alueen pinta-ala. Kun
rajoittaman alueen pinta-ala. Kun 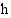 on hyvin pieni, tämä pinta-ala on likimäärin yhtä suuri kuin suorakulmio, jonka kanta on
on hyvin pieni, tämä pinta-ala on likimäärin yhtä suuri kuin suorakulmio, jonka kanta on 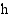 ja korkeus
ja korkeus 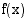 . Tämän pinta-ala on
. Tämän pinta-ala on 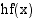 , joten
, joten
Tämä approksimaatio on sitä parempi mitä pienempi 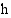 on. Kun
on. Kun 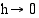 , arvion virhe lähestyy myös nollaa, joten
, arvion virhe lähestyy myös nollaa, joten
Pinta-alafunktio 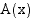 siis jokin funktion
siis jokin funktion 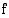 integraalifunktio. Oletetaan, että funktio
integraalifunktio. Oletetaan, että funktio 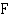 on eräs funktion
on eräs funktion 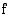 integraalifunktio. Tällöin kaikki
integraalifunktio. Tällöin kaikki 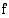 :n integraalifunktiot ovat muotoa
:n integraalifunktiot ovat muotoa 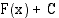 , missä
, missä 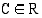 , ja erityisesti pinta-alafunktio
, ja erityisesti pinta-alafunktio 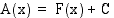 jollakin
jollakin 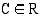 . Koska
. Koska 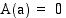 , on
, on
kaikilla 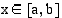 . Tästä seuraa, että funktion
. Tästä seuraa, että funktion 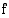 kuvaajan,
kuvaajan, 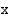 -akselin sekä suorien
-akselin sekä suorien 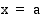 ja
ja 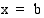 rajoittaman alueen pinta-ala
rajoittaman alueen pinta-ala
missä 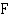 on jokin funktion
on jokin funktion 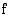 integraalifunktio.
integraalifunktio.
arvon laskeminen analyysin peruslauseen nojalla on kaksivaiheinen:
• määrätään jokin funktion 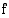 integraalifunktio
integraalifunktio 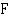 ja
ja
Vaiheessa, jossa funktio 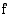 on integroitu, mutta arvoja
on integroitu, mutta arvoja 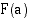 ja
ja 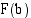 ei ole vielä laskettu käytetään merkintää
ei ole vielä laskettu käytetään merkintää
joka tarkoittaa erotusta 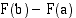 . Merkintä luetaan: "sijoitus
. Merkintä luetaan: "sijoitus 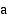 :sta
:sta 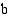 :hen
:hen 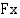 ". Siis
". Siis