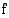 jatkuva suljetulla välillä
jatkuva suljetulla välillä 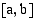 . Jaetaan väli
. Jaetaan väli 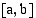 edellisen esimerkin tapaan
edellisen esimerkin tapaan 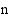 osaväliin. Merkitään jakopisteitä tunnuksin
osaväliin. Merkitään jakopisteitä tunnuksin 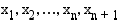 , missä
, missä 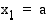 ja
ja 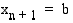 . Osavälien pituudet olkoot
. Osavälien pituudet olkoot 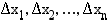 , missä
, missä 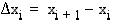 kaikilla
kaikilla 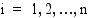 . Muodostetaan summa
. Muodostetaan summa
Olkoon funktio 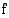 jatkuva suljetulla välillä
jatkuva suljetulla välillä 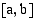 . Jaetaan väli
. Jaetaan väli 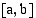 edellisen esimerkin tapaan
edellisen esimerkin tapaan 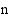 osaväliin. Merkitään jakopisteitä tunnuksin
osaväliin. Merkitään jakopisteitä tunnuksin 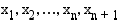 , missä
, missä 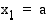 ja
ja 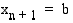 . Osavälien pituudet olkoot
. Osavälien pituudet olkoot 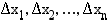 , missä
, missä 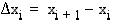 kaikilla
kaikilla 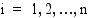 . Muodostetaan summa
. Muodostetaan summa
Kun jakopisteiden lukumäärä 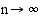 ja jakovälin pituus
ja jakovälin pituus 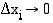 kaikilla
kaikilla 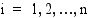 , summa
, summa 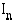 lähestyy raja-arvoa, joka on funktion
lähestyy raja-arvoa, joka on funktion 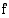 määrätty integraali
määrätty integraali 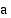 :sta
:sta 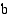 :hen ja jota merkitään
:hen ja jota merkitään
Funktion 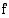 määrätty integraali
määrätty integraali 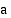 :sta
:sta 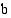 :hen on siis raja-arvo
:hen on siis raja-arvo
jos tämä raja-arvo on olemassa. Lukuja 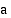 ja
ja 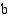 kutsutaan
integroimisrajoiksi:
kutsutaan
integroimisrajoiksi: 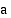 on alaraja ja
on alaraja ja 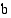 on yläraja.
on yläraja.
Johdantoesimerkissä saatu raja-arvo, joka ilmoittaa yrityksen tuotannon määrän tarkasteltavien 30 vuorokauden aikana, on tuotantonopeusfunktion 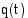 määrätty integraali 0:sta 30:een, jota merkitään
määrätty integraali 0:sta 30:een, jota merkitään
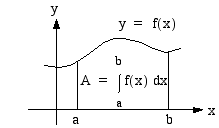 Geometrisesti tulkittuna funktion
Geometrisesti tulkittuna funktion 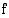 määrätty integraali
määrätty integraali 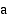 :sta
:sta 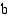 :hen on
itseisarvoltaan funktion
:hen on
itseisarvoltaan funktion 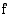 kuvaajan,
kuvaajan, 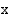 -akselin sekä suorien
-akselin sekä suorien 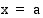 ja
ja 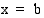 rajoittaman alueen pinta-ala. Tämä on ymmärrettävissä seuraavasti. Jos funktio
rajoittaman alueen pinta-ala. Tämä on ymmärrettävissä seuraavasti. Jos funktio 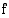 on välillä
on välillä 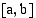 jatkuva ja ei-negatiivinen, summan
jatkuva ja ei-negatiivinen, summan 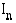 termit
termit 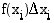 ilmoittavat sen suorakulmion pinta-alan, jonka kanta on jakovälin pituus
ilmoittavat sen suorakulmion pinta-alan, jonka kanta on jakovälin pituus 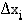 ja korkeus funktion arvo jakovälin alkupisteessä
ja korkeus funktion arvo jakovälin alkupisteessä 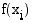 . Tällöin summa
. Tällöin summa
on likiarvo funktion 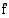 kuvaajan,
kuvaajan, 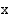 -akselin sekä suorien
-akselin sekä suorien 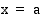 ja
ja 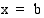 rajoittaman alueen pinta-alalle.
rajoittaman alueen pinta-alalle.
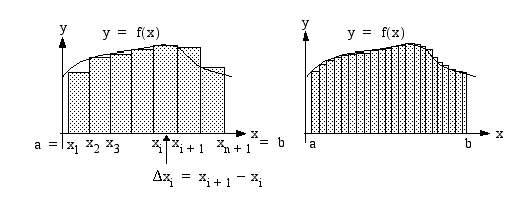
Arvio paranee, kun jakovälien lukumäärä kasvaa ja jakovälin pituus pienenee. Alueen pinta-ala on siten summan 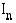 raja-arvo, kun
raja-arvo, kun 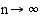 ja
ja 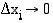 kaikilla
kaikilla 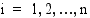 :
:
Edellä oletettiin, että funktio 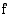 on ei-negatiivinen välillä
on ei-negatiivinen välillä 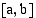 . Jos
. Jos 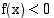 kaikilla
kaikilla 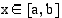 , niin määrätty integraali
, niin määrätty integraali
ja se on itseisarvoltaan yhtä suuri kuin funktion kuvaajan, 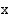 -akselin sekä suorien
-akselin sekä suorien 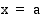 ja
ja 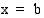 rajoittaman alueen pinta-ala.
rajoittaman alueen pinta-ala.
Määrätyn integraalin laskeminen summan raja-arvona on työlästä ja vaatii yleensä tehokkaan laskulaitteen käyttämistä. Poikkeuksena ovat sellaiset erikoistapaukset, joissa määrätty integraali voidaan laskea geometrisesti pinta-alana. Seuraava lause tarjoaa yksinkertaisemman tavan määrätyn integraalin laskemiseksi.