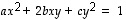 .
(1)
.
(1)Tarkastellaan ensin kahden muuttujan toisen asteen (tasa-asteista) yhtälöä
Sen vasenta puolta sanotaan kahden muuttujan neliömuodoksi. Tämä yhtälö voidaan kirjoittaa matriisimuotoon
missä alkuperäinen termin 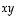 kerroin
kerroin 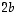 on jaettu kahteen paikkaan, jotta saadusta kerroinmatriisista
on jaettu kahteen paikkaan, jotta saadusta kerroinmatriisista
tulee symmetrinen. Silloin se voidaan nimittäin lauseen 11.5 mukaan diagonalisoida, ts. on olemassa ortonormaali tason kanta 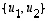 niin, että
niin, että
Tässä matriisi 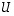 muodostuu, kuten edellisessä luvussa johdettiin, ominaisvektoreista ja matriisi
muodostuu, kuten edellisessä luvussa johdettiin, ominaisvektoreista ja matriisi 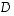 ominaisarvoista:
ominaisarvoista:
Lisäksi 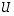 on ortogonaalinen matriisi, jolloin siis
on ortogonaalinen matriisi, jolloin siis 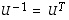 .
Toisaalta tietenkin ominaisarvoyhtälöt
.
Toisaalta tietenkin ominaisarvoyhtälöt 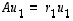 ja
ja 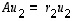 pätevät.
pätevät.
Nyt matriisi 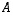 voidaan esittää muodossa
voidaan esittää muodossa 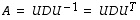 ,
joten yhtälö (2) voidaan muuttaa muotoon
,
joten yhtälö (2) voidaan muuttaa muotoon
eli toisin kirjoitettuna muotoon
Tässä kaarisuluissa esiintyvä tulo antaa itse asiassa lauseen 9.2 mukaan vektorin 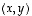 koordinaatit
koordinaatit 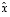 ja
ja 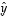 kannassa
kannassa 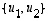 ,
ts.
,
ts.
Tämä yhtälö määrittelee siis aivan saman ratkaisujoukon kuin yhtälö (1), nyt vain ratkaisuvektorien koordinaatit on ilmoitettu vektorien 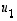 ja
ja 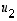 muodostamassa kannassa eikä enää luonnollisessa kannassa.
muodostamassa kannassa eikä enää luonnollisessa kannassa.
saatettua muotoa sanotaan neliömuodon normaalimuodoksi tai pääakseliesitykseksi. Ominaisvektoreiden määräämät suorat ovat silloin neliömuodon pääakselit. Kaikissa tapauksissa saatava käyrä on symmetrinen pääakselien suhteen. Mahdolliset pääakseliesitykset voidaan luokitella esimerkiksi seuraavasti.
(1) Jos ominaisarvot ovat molemmat positiivisia, esitys saadaan muotoon
ja kyseessä on silloin
ellipsi, jonka puoliakselien pituudet ovat 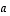 ja
ja 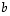 .
.
(2) Jos ominaisarvot ovat erimerkkiset, esitys saadaan muotoon
ja kyseessä on silloin (kummassakin tapauksessa) hyperbeli. Se aukeaa sen muuttujan akselin suuntaan, jonka kerroin on positiivinen.
(3) Jos toinen ominaisarvoista on positiivinen ja toinen nolla, esitys saadaan muotoon
ja kyseessä on silloin kaksi yhdensuuntaista suoraa - kaksi pystysuoraa tai kaksi vaakasuoraa.
(4) Muut tapaukset ovat vielä surkastuneempia käyriä tai sitten mahdottomia yhtälöitä.
muuttujien kertoimista saadaan symmetrinen matriisi (kun 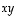 -kerroin puolitetaan)
-kerroin puolitetaan)
jonka karakteristinen yhtälö on
Edelleen tämän ratkaisut eli matriisin 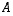 ominaisarvot ovat
ominaisarvot ovat
Ratkaistaan sitten ominaisvektorit ominaisarvoyhtälöistä. Ensiksi ominaisarvolle 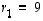 saadaan:
saadaan:
Valitaan saadusta ratkaisusta ykkösen pituiseksi ominaisvektoriksi
Toiseksi ominaisarvolle 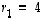 saadaan:
saadaan:
Valitaan nyt ykkösen pituiseksi ominaisvektoriksi
Koordinaatistossa 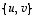 yhtälö
yhtälö 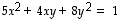 saa siten muodon
saa siten muodon
Tämä yhtälö, kuten myös alkuperäinen yhtälö, esittää näin ollen ellipsiä, jonka puoliakselit ovat pituudeltaan 1/3 ja 1/2. Edellinen on vektorin 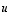 suuntaan ja jälkimmäinen vektorin
suuntaan ja jälkimmäinen vektorin 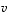 suuntaan. Piirrä itsellesi havainnollistava kuva!
suuntaan. Piirrä itsellesi havainnollistava kuva!