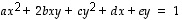,
(1*)Tarkastellaan sitten yleistä toisen asteen yhtälöä
jossa esiintyy siis edellisen tapauksen lisäksi myös ensimmäisen asteen termejä. Tällaisen yhtälön tutkiminen voidaan aloittaa kuten edellä, ts. etsitään ensin vastaavaan tasa-asteiseen toisen asteen yhtälöön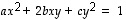 
liittyvä pääakselimuoto
Tämän jälkeen sijoitetaan muuttujien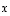 
ja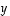 
riippuvuudet muuttujista 
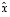ja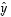 
yhtälöön (1*). Lopuksi yritetään saatua yhtälöä muuntaa, yleensä neliöön täydentämällä, sievempään muotoon. Edellä olevien luokitukseen on nyt otettava oleellisena lisäyksenä seuraava mahdollisuus.
(5) Jos toinen ominaisarvoista on positiivinen ja toinen nolla, esitys voidaan silloin saada tapauksen (3) lisäksi myös muotoon
ja kyseessä on silloin (kaikissa näissä tapauksissa) paraabeli. Se aukeaa sen muuttujan akselin suuntaan, joka esiintyy ilman neliöön korotusta.
määräämää käyrää. Tämän yhtälön neliöosa on sama kuin esimerkissä 12.1, joten sieltä kopioidaan, että koordinaatistossa
Muuttujien vaihtoa sitoo yhteen ehto
joten koko alkuperäinen yhtälö saadaan nyt muotoon
Täydennetään sitten vasen puoli neliöiden summaksi, jolloin saadaan yhtälö
saadaan lopulta pääakseliesitykseksi
Tästä näkyykin, että kyseessä on ellipsi. Sen keskipiste on pisteessä
sen pääakselit ovat vektorien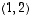 
ja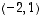 
suuntaiset (kulkien keskipisteen kautta) ja sen puoliakselien pituudet 
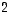ja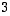 
.
Piirrä itsellesi havainnollistava kuva!
Edellä on tarkasteltu kahden muuttujan neliömuotoja. Samantapaista tarkastelua voidaan soveltaa useammankin muuttujan avulla muodostettuihin neliömuotolausekkeisiin. Nämä yhtälöt voidaan yleisesti kirjoittaa muotoon
missä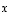 
on muuttujista 
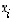muodostuva avaruuden 
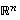vektori, 
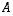on toisen asteen termien kertoimista (osa puolitettuna) muodostuva symmetrinen neliömatriisi ja 
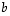on ensimmäisen asteen termien kertoimista muodostettu vektori.
Tällaisen yleisen toisen asteen yhtälön selvittäminen voidaan periaatteessa tehdä samalla tavalla kuin kahdelle muuttujalle, ts. diagonalisoidaan ensin matriisi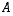 
,
vaihdetaan diagonalisoinnissa tehdyn kannanvaihdon mukaisesti muuttujat ja yritetään sitten neliöimisillä saada näiden muuttujien ensimmäisen asteen termit pois. Esimerkiksi avaruudessa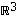 
tulokseksi saadaan, että toisen asteen yhtälöt esittävät erilaisia pintoja, kuten ellipsoideja, hyperboloideja, paraboloideja, tasoja jne. Tarkemmat tarkastelut jätetään kuitenkin tässä yhteydessä tekemättä.
.
on muotoa 
.
,
.
.
.
,
,