1.1.  Joukko-opin merkintöjä

Tässä ensimmäisessä pykälässä esitämme muutamia tuttuja joukko-opin perusasioita, lähinnä nimityksien ja merkintätapojen kertaamiseksi.

Yleensä tarkasteltavat joukot tulevat olemaan jonkin tunnetun perusjoukon 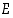osajoukkoja. Ne ilmoitetaan silloin muodossa

,

jossa alkion sisältyvyyttä joukkoon merkitään symbolilla ja annetulla ehdolla rajataan se, mitkä alkiot joukkoon otetaan mukaan. Joukko, jossa on äärellisen monta alkiota, voidaan ilmoittaa myös luettelemalla sen alkiot, kuten esimerkiksi 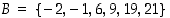. Luettelomaisesti voidaan ilmaista usein myös joukko, jossa on ääretön määrä alkioita, mikäli esitetty luettelon osa ilmaisee selkeän säännön, jolla joukkoon kuuluvat alkiot määräytyvät. Esimerkiksi parillisten kokonaislukujen joukko voidaan esittää muodossa .

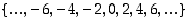Tuttuja (perus)joukkoja ovat muun muassa

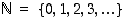= luonnolliset luvut (eli lukumääräluvut),

= kokonaisluvut,

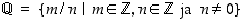= rationaaliluvut eli murtoluvut ja

= reaaliluvut.

Reaalilukujen muodostumista selitetään enemmän pykälässä Rationaali- ja reaaliluvuista.

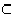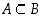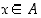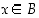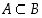Joukkojen sisältyvyys eli inkluusio () määritellään seuraavasti: , jos ehdosta seuraa aina, että . Kun , niin 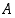on joukon 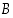osajoukko. Joukot ovat yhtäsuuret eli samat, 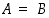, jos sek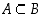ä että 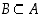. Huomaa, että sisältyvyys ei kiellä sitä mahdollisuutta, että joukot jo olisivat samoja, eli sisältyvyyden ei tarvitse olla aitoa. Yllä oleville lukujoukoille pätevät perättäiset inkluusiot 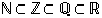ja näistä jokainen on aito sisältyvyys.

Kahdelle perusjoukon 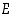osajoukolle 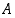ja 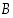voidaan muodostaa

yhdiste ,

leikkaus ja

erotus .

Joukoista voidaan muodostaa myös tulojoukkoja eli karteesisia tuloja

,

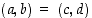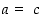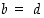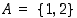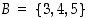minkä määrittelyssä esiintyville järjestetyille pareille sovitaan, että täsmälleen silloin, kun ja . Esimerkiksi joukoille ja on

.

Jos tulojoukossa 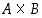on erikoisesti 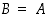, merkitään myös 'potenssimaisesti', että 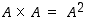. Esimerkiksi reaalilukujen tulojoukkoa 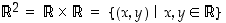havainnollistetaan kuvan 1 mukaisesti tasona.

Kuva 1.

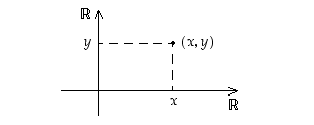
Tasoa käsitellään tarkemmin pykälässä Koordinaattitaso.