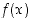 on määritelty ja jatkuva kaikilla reaalisilla
on määritelty ja jatkuva kaikilla reaalisilla 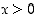 . Koska
. Koska
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Funktio 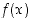 on määritelty ja jatkuva kaikilla reaalisilla
on määritelty ja jatkuva kaikilla reaalisilla 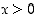 . Koska
. Koska
(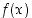 on derivoituva kaikilla reaalisilla
on derivoituva kaikilla reaalisilla 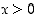 .) Edelleen
.) Edelleen
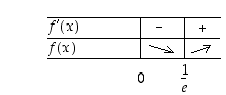
Funktio 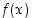 on aidosti vähenevä, kun
on aidosti vähenevä, kun 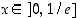 ja aidosti kasvava kun
ja aidosti kasvava kun 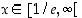 . Lisäksi
. Lisäksi
Jälkimmäinen seuraa siitä, että
Funktiolla 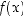 on yksi ääriarvo, joka on globaali minimi kohdassa
on yksi ääriarvo, joka on globaali minimi kohdassa 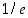 ,
ja sen arvo on
,
ja sen arvo on
[Opiskelutehtävä 36] [Vinkki tehtävään 36]