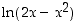on määritelty, kun 
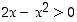eli 
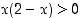. Selvitetään ensin milloin 
,
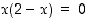ja päätellään sitten määrittelyjoukko toisen asteen käyrän kuvaajan avulla. Nollakohdat:
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
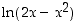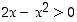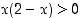Lauseke on määritelty, kun eli . Selvitetään ensin milloin ,
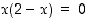ja päätellään sitten määrittelyjoukko toisen asteen käyrän kuvaajan avulla. Nollakohdat:
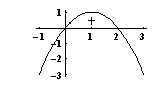
Lauseke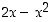 
on siten alaspäin aukeava paraabeli ja saa täten positiivisia arvoja vain nollakohtiensa välissä. Näin ollen 
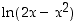on määritelty, kun 
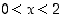. Derivoidaan se:
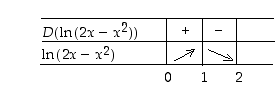
Lauseke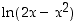 
saa maksimiarvon kohdassa 
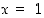; kyseinen arvo on 
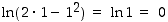. Minimiarvoa lauseke ei saa (huomaa, että määrittelyjoukkona on avoin väli).
[Opiskelutehtävä 34] [Vinkki tehtävään 34]
