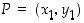 ja
ja 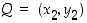 eivät ole samalla pystysuoralla, ts.
eivät ole samalla pystysuoralla, ts. 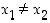 . Näiden pisteiden kautta kulkevan suoran kulmakerroin (kaltevuussuhde, jyrkkyys) on suhde
. Näiden pisteiden kautta kulkevan suoran kulmakerroin (kaltevuussuhde, jyrkkyys) on suhde
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Oletetaan sitten, että pisteet 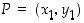 ja
ja 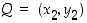 eivät ole samalla pystysuoralla, ts.
eivät ole samalla pystysuoralla, ts. 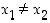 . Näiden pisteiden kautta kulkevan suoran kulmakerroin (kaltevuussuhde, jyrkkyys) on suhde
. Näiden pisteiden kautta kulkevan suoran kulmakerroin (kaltevuussuhde, jyrkkyys) on suhde
ja tämän suoran yhtälö saadaan ehdosta
Esimerkiksi pisteiden 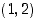 ja
ja 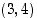 kautta kulkevan suoran yhtälö on
kautta kulkevan suoran yhtälö on
Kun suoran yhtälö on muodossa 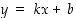 ,
on
,
on 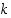 sen kulmakerroin sekä
sen kulmakerroin sekä 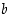 sen ja
sen ja 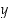 −akselin leikkauspisteen arvo. Pystysuoran eli
−akselin leikkauspisteen arvo. Pystysuoran eli 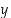 −akselin suuntaisen suoran yhtälö on muotoa
−akselin suuntaisen suoran yhtälö on muotoa 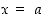 . Sille ei määritellä kulmakerrointa. Vaakasuoran eli
. Sille ei määritellä kulmakerrointa. Vaakasuoran eli 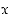 −akselin suuntaisen suoran kulmakerroin on nolla.
−akselin suuntaisen suoran kulmakerroin on nolla.
Kaksi tason suoraa ovat yhdensuuntaiset, jos niiden kulmakertoimet ovat samat. Lisäksi kaikki pystysuorat ovat keskenään yhdensuuntaiset.
Suoraa 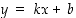 ,
joka ei ole vaakasuora, vastaan kohtisuorassa ovat kaikki sellaiset suorat, joiden yhtälö on muotoa
,
joka ei ole vaakasuora, vastaan kohtisuorassa ovat kaikki sellaiset suorat, joiden yhtälö on muotoa 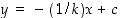 . Tämä tulos näkyy seuraavasta: Koska origon kautta kulkeva suora
. Tämä tulos näkyy seuraavasta: Koska origon kautta kulkeva suora 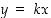 kulkee myös pisteen
kulkee myös pisteen 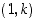 kautta, kulkee sitä vastaan kohtisuorassa oleva, origon kautta kulkeva suora pisteen
kautta, kulkee sitä vastaan kohtisuorassa oleva, origon kautta kulkeva suora pisteen 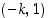 kautta (jos nimittäin tasoa kierretään
kautta (jos nimittäin tasoa kierretään 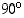 vastapäivään, muuttuvat pisteiden vaakakoordinaatit pystykoordinaateiksi ja pystykoordinaatit vastakkaismerkkisiksi vaakakoordinaateiksi). Yhdensuuntaissiirroin tilanne saadaan siirrettyä origosta mielivaltaiseen
vastapäivään, muuttuvat pisteiden vaakakoordinaatit pystykoordinaateiksi ja pystykoordinaatit vastakkaismerkkisiksi vaakakoordinaateiksi). Yhdensuuntaissiirroin tilanne saadaan siirrettyä origosta mielivaltaiseen 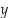 −akselin leikkauspisteeseen. Kaksi suoraa (jotka eivät ole pysty- eikä vaakasuoria) ovat siten kohtisuorassa toisiaan vastaan, mikäli niiden kulmakertoimien tulo on −1 (ks. myös harjoitustehtävä 28). Lisäksi pystysuorat ja vaakasuorat ovat keskenään kohtisuorassa toisiaan vastaan.
−akselin leikkauspisteeseen. Kaksi suoraa (jotka eivät ole pysty- eikä vaakasuoria) ovat siten kohtisuorassa toisiaan vastaan, mikäli niiden kulmakertoimien tulo on −1 (ks. myös harjoitustehtävä 28). Lisäksi pystysuorat ja vaakasuorat ovat keskenään kohtisuorassa toisiaan vastaan.