I.4. Joukko-oppia
Yksinkertaisesti ilmaistuna joukko tunnistetaan alkioistaan. Kun alkio
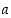 on joukon
on joukon
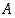 alkio, merkitään
alkio, merkitään 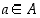 . Yleisin tapa määritellä joukko on ilmoittaa se jonkin tunnetun joukon osajoukoksi. Alkioiden valinta voidaan ilmoittaa jollakin lausekkeella, ominaisuudella tai ehdolla. Esimerkiksi
. Yleisin tapa määritellä joukko on ilmoittaa se jonkin tunnetun joukon osajoukoksi. Alkioiden valinta voidaan ilmoittaa jollakin lausekkeella, ominaisuudella tai ehdolla. Esimerkiksi 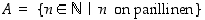 tarkoittaa sitä luonnollisten lukujen osajoukkoa, jonka alkiot toteuttavat annetun ehdon, parillisuuden. Valinta voidaan tehdä myös luettelemalla joukkoon kuuluvat alkiot, kuten esimerkiksi
tarkoittaa sitä luonnollisten lukujen osajoukkoa, jonka alkiot toteuttavat annetun ehdon, parillisuuden. Valinta voidaan tehdä myös luettelemalla joukkoon kuuluvat alkiot, kuten esimerkiksi 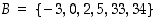 tai
tai 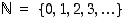 . Varsinainen joukon käsitteen aksiomaattinen määrittely on työläs ja ehdotonta tarkkuutta vaativa. Kaikki ajateltavissa olevat ilmaisut eivät silti tuota matemaattisesti mielekästä joukkoa, ei esimerkiksi ole olemassa kaikkien joukkojen joukkoa.
. Varsinainen joukon käsitteen aksiomaattinen määrittely on työläs ja ehdotonta tarkkuutta vaativa. Kaikki ajateltavissa olevat ilmaisut eivät silti tuota matemaattisesti mielekästä joukkoa, ei esimerkiksi ole olemassa kaikkien joukkojen joukkoa.
Joukko
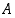 on joukon
on joukon
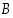 osajoukko eli
osajoukko eli
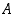 sisältyy joukkoon
sisältyy joukkoon
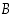 ,
jos kaikki sen alkiot ovat myös joukon
,
jos kaikki sen alkiot ovat myös joukon
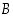 alkioita:
alkioita:
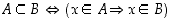 .
.
Kaksi joukkoa ovat samat, jos kumpikin on toisensa osajoukko eli jos kumpikin sisältää toistensa alkiot:
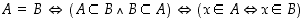 .
.
Huomaa, että merkintä 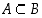 pitää sisällään sen mahdollisuuden, että
pitää sisällään sen mahdollisuuden, että 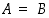 . Jos
. Jos 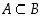 ,
mutta
,
mutta 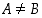 ,
on joukko
,
on joukko
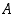 joukon
joukon
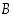 aito osajoukko, merkitään
aito osajoukko, merkitään 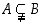 .
Tyhjä
joukko
.
Tyhjä
joukko 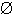 on joukko, jossa ei ole alkioita. Se on aina jokaisen joukon osajoukko.
on joukko, jossa ei ole alkioita. Se on aina jokaisen joukon osajoukko.
Yllä joukkojen sisältyvyys ja samuus määriteltiin implikaation ja ekvivalenssin avulla. Käyttäen muita loogisia siteitä määrittelyehtoihin saadaan määriteltyä joukkojen
komplementti,
leikkaus ja
yhdiste seuraavaan tapaan.
Jos
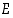 on ns. perusjoukko, jonka osajoukkoja tarkasteltavat joukot
on ns. perusjoukko, jonka osajoukkoja tarkasteltavat joukot 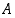 ja
ja 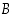 ovat, asetetaan
leikkaus
ovat, asetetaan
leikkaus 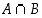 ja
yhdiste
ja
yhdiste 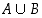 seuraavasti:
seuraavasti:
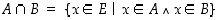 ja
ja 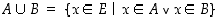 .
.
Jos 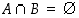 ,
ovat joukot
,
ovat joukot 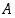 ja
ja 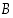 erilliset.
erilliset.
Joukoille voidaan muodostaa myös ns.
joukkoerotus:
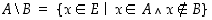 .
.
Sitä sanotaan myös joukon 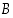 komplementiksi joukossa
komplementiksi joukossa 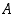 . Osajoukon
. Osajoukon 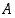 komplementtia
komplementtia 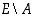 koko perusjoukossa merkitään myös
koko perusjoukossa merkitään myös 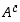 .
.
Kolmesta mielivaltaisesta joukosta 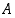
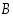 ja
ja 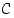 leikkauksilla ja yhdisteillä saatavat erilliset alkeisjoukot näkyvät seuraavasta ns.
Vennin
kuviosta. Siinä joukot
leikkauksilla ja yhdisteillä saatavat erilliset alkeisjoukot näkyvät seuraavasta ns.
Vennin
kuviosta. Siinä joukot 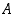 ,
,
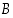 ja
ja 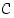 ovat keskenään siinä mielessä mahdollisimman yleisessä asennossa, että kaikki näiden avulla muodostettavat kahdeksan erillistä osajoukkoa näkyvät. Vennin kuvioiden avulla voidaankin sen takia yleispätevästi katsoa, päteekö jokin korkeintaan kolmea joukkoa koskeva väite paikkansa, esimerkiksi vaikkapa seuraavan opiskelutehtävän väite.
ovat keskenään siinä mielessä mahdollisimman yleisessä asennossa, että kaikki näiden avulla muodostettavat kahdeksan erillistä osajoukkoa näkyvät. Vennin kuvioiden avulla voidaankin sen takia yleispätevästi katsoa, päteekö jokin korkeintaan kolmea joukkoa koskeva väite paikkansa, esimerkiksi vaikkapa seuraavan opiskelutehtävän väite.
Opiskelutehtävä 7. (Joukko-opillinen väite)
Tutki, pitääkö väite 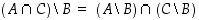 aina paikkansa.
aina paikkansa.
Vinkki tehtävään 7
Opiskelutehtävä 8. (Vennin kuvion palat)
Olkoot 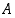 ,
,
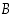 ja
ja 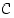 saman perusjoukon
saman perusjoukon 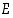 osajoukkoja. Valitse Vennin kuviosta jotkin kaksi palaa, jotka eivät sivua toisiaan, ja esitä näiden yhdiste joukkojen
osajoukkoja. Valitse Vennin kuviosta jotkin kaksi palaa, jotka eivät sivua toisiaan, ja esitä näiden yhdiste joukkojen 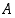 ,
,
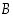 ja
ja 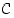 avulla vähintään kahdella eri tavalla.
avulla vähintään kahdella eri tavalla.
Vinkki tehtävään 8
Opiskelutehtävä 9. (Joukkojen sisältymisen vastakohta)
Mitä tarkoittaa mielestäsi merkintä 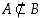 ? Selitä se sanallisesti ja alkioittain määriteltynä sekä anna esimerkki tällaisesta joukkotilanteesta.
? Selitä se sanallisesti ja alkioittain määriteltynä sekä anna esimerkki tällaisesta joukkotilanteesta.
Vinkki tehtävään 9
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
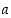 on joukon
on joukon
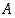 alkio, merkitään
alkio, merkitään 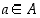 . Yleisin tapa määritellä joukko on ilmoittaa se jonkin tunnetun joukon osajoukoksi. Alkioiden valinta voidaan ilmoittaa jollakin lausekkeella, ominaisuudella tai ehdolla. Esimerkiksi
. Yleisin tapa määritellä joukko on ilmoittaa se jonkin tunnetun joukon osajoukoksi. Alkioiden valinta voidaan ilmoittaa jollakin lausekkeella, ominaisuudella tai ehdolla. Esimerkiksi 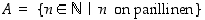 tarkoittaa sitä luonnollisten lukujen osajoukkoa, jonka alkiot toteuttavat annetun ehdon, parillisuuden. Valinta voidaan tehdä myös luettelemalla joukkoon kuuluvat alkiot, kuten esimerkiksi
tarkoittaa sitä luonnollisten lukujen osajoukkoa, jonka alkiot toteuttavat annetun ehdon, parillisuuden. Valinta voidaan tehdä myös luettelemalla joukkoon kuuluvat alkiot, kuten esimerkiksi 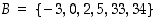 tai
tai 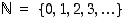 . Varsinainen joukon käsitteen aksiomaattinen määrittely on työläs ja ehdotonta tarkkuutta vaativa. Kaikki ajateltavissa olevat ilmaisut eivät silti tuota matemaattisesti mielekästä joukkoa, ei esimerkiksi ole olemassa kaikkien joukkojen joukkoa.
. Varsinainen joukon käsitteen aksiomaattinen määrittely on työläs ja ehdotonta tarkkuutta vaativa. Kaikki ajateltavissa olevat ilmaisut eivät silti tuota matemaattisesti mielekästä joukkoa, ei esimerkiksi ole olemassa kaikkien joukkojen joukkoa. 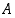 on joukon
on joukon
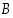 osajoukko
osajoukko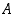 sisältyy joukkoon
sisältyy joukkoon
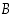 ,
jos kaikki sen alkiot ovat myös joukon
,
jos kaikki sen alkiot ovat myös joukon
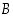 alkioita:
alkioita: 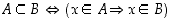 .
. 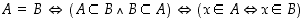 .
.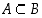 pitää sisällään sen mahdollisuuden, että
pitää sisällään sen mahdollisuuden, että 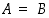 . Jos
. Jos 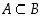 ,
mutta
,
mutta 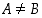 ,
on joukko
,
on joukko
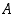 joukon
joukon
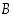 aito
aito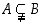 .
Tyhjä
joukko
.
Tyhjä
joukko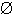 on joukko, jossa ei ole alkioita. Se on aina jokaisen joukon osajoukko.
on joukko, jossa ei ole alkioita. Se on aina jokaisen joukon osajoukko. 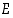 on ns.
on ns. 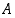 ja
ja 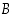 ovat, asetetaan
leikkaus
ovat, asetetaan
leikkaus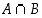 ja
yhdiste
ja
yhdiste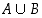 seuraavasti:
seuraavasti: 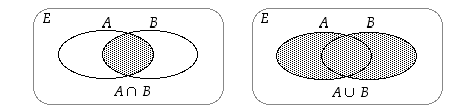
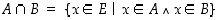 ja
ja 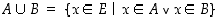 .
. 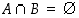 ,
ovat joukot
,
ovat joukot 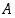 ja
ja 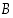 erilliset
erilliset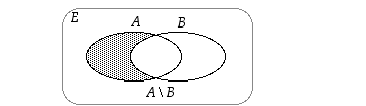
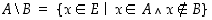 .
. 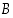 komplementiksi
komplementiksi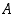 . Osajoukon
. Osajoukon 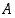 komplementtia
komplementtia 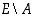 koko perusjoukossa merkitään myös
koko perusjoukossa merkitään myös 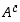 .
. 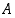
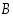 ja
ja 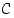 leikkauksilla ja yhdisteillä saatavat erilliset alkeisjoukot näkyvät seuraavasta ns.
Vennin
leikkauksilla ja yhdisteillä saatavat erilliset alkeisjoukot näkyvät seuraavasta ns.
Vennin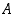 ,
,
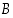 ja
ja  ovat keskenään siinä mielessä mahdollisimman yleisessä asennossa, että kaikki näiden avulla muodostettavat kahdeksan erillistä osajoukkoa näkyvät. Vennin kuvioiden avulla voidaankin sen takia yleispätevästi katsoa, päteekö jokin korkeintaan kolmea joukkoa koskeva väite paikkansa, esimerkiksi vaikkapa seuraavan opiskelutehtävän väite.
ovat keskenään siinä mielessä mahdollisimman yleisessä asennossa, että kaikki näiden avulla muodostettavat kahdeksan erillistä osajoukkoa näkyvät. Vennin kuvioiden avulla voidaankin sen takia yleispätevästi katsoa, päteekö jokin korkeintaan kolmea joukkoa koskeva väite paikkansa, esimerkiksi vaikkapa seuraavan opiskelutehtävän väite. 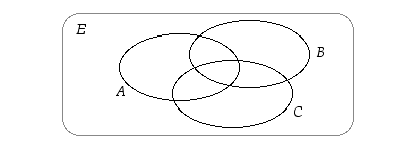
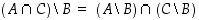 aina paikkansa.
aina paikkansa. 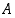 ,
,
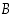 ja
ja 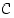 saman perusjoukon
saman perusjoukon 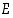 osajoukkoja. Valitse Vennin kuviosta jotkin kaksi palaa, jotka eivät sivua toisiaan, ja esitä näiden yhdiste joukkojen
osajoukkoja. Valitse Vennin kuviosta jotkin kaksi palaa, jotka eivät sivua toisiaan, ja esitä näiden yhdiste joukkojen 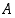 ,
,
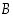 ja
ja 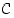 avulla vähintään kahdella eri tavalla.
avulla vähintään kahdella eri tavalla. 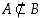 ? Selitä se sanallisesti ja alkioittain määriteltynä sekä anna esimerkki tällaisesta joukkotilanteesta.
? Selitä se sanallisesti ja alkioittain määriteltynä sekä anna esimerkki tällaisesta joukkotilanteesta. 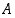 ,
,
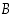 ja
ja 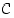 saman perusjoukon
saman perusjoukon 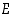 osajoukkoja. Osoita oikeaksi ns. osittelulaki
osajoukkoja. Osoita oikeaksi ns. osittelulaki 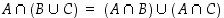 .
. 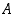 ja
ja 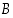 saman perusjoukon
saman perusjoukon 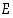 osajoukkoja. Osoita oikeaksi ns. de
osajoukkoja. Osoita oikeaksi ns. de 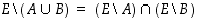 .
.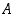 ,
,
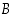 ja
ja 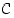 saman perusjoukon
saman perusjoukon 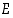 osajoukkoja. Määrää Vennin kuviosta joukko
osajoukkoja. Määrää Vennin kuviosta joukko 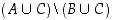 .
.