I.3. Predikaattilogiikkaa
Jos jokin lause
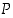 riippuu jostain muuttujasta
riippuu jostain muuttujasta 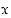 ,
ilmoitamme riippuvuuden kirjoittamalla
,
ilmoitamme riippuvuuden kirjoittamalla 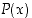 ja sanomme, että se on
avoin lause. Esimerkiksi
ja sanomme, että se on
avoin lause. Esimerkiksi 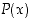 voi olla kokonaisluvusta
voi olla kokonaisluvusta 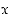 riippuva lause "
riippuva lause "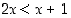 ". Jos tässä muuttujalle
". Jos tässä muuttujalle 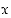 annetaan jokin arvo, avoin lause
annetaan jokin arvo, avoin lause 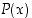 muuttuu lauseeksi, jolla on jokin totuusarvo, joko tosi tai epätosi.
muuttuu lauseeksi, jolla on jokin totuusarvo, joko tosi tai epätosi.
Avoin lause 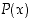 voi siis saada kumpiakin totuusarvoja, ts. voi olla olemassa arvo
voi siis saada kumpiakin totuusarvoja, ts. voi olla olemassa arvo 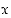 ,
jolle
,
jolle 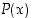 on tosi, ja voi olla olemassa arvo
on tosi, ja voi olla olemassa arvo 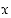 ,
jolle
,
jolle 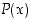 on epätosi. Tällainen on edellä mainittu lause "
on epätosi. Tällainen on edellä mainittu lause "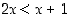 ".
".
On toisaalta helppo keksiä avoin lause, joka on tosi kaikilla muuttujansa arvoilla. Esimerkiksi kokonaisluvusta riippuva lause "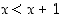 " on sellainen. Vastaavasti lause "
" on sellainen. Vastaavasti lause "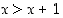 " on aina epätosi.
" on aina epätosi.
Matematiikassa edellisten kaltaiset tilanteet ovat itse asiassa varsin tavallisia ja siksi niitä varten on otettu käyttöön omat operaatiosymbolit:
olemassaolokvanttori (∃) ja
kaikki- eli
universaalikvanttori (∀). Merkitäänkin 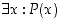 ,
kun tarkoitetaan, että on olemassa
,
kun tarkoitetaan, että on olemassa 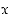 ,
jolla on ominaisuus
,
jolla on ominaisuus 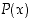 . Vastaavasti merkintä
. Vastaavasti merkintä 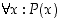 tarkoittaa, että kaikilla
tarkoittaa, että kaikilla 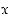 on ominaisuus
on ominaisuus 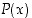 . Jos näissä lausumissa muuttuja
. Jos näissä lausumissa muuttuja 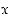 halutaan rajata johonkin joukkoon tai luokkaan
halutaan rajata johonkin joukkoon tai luokkaan 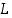 ,
merkitään silloin täsmennettynä
,
merkitään silloin täsmennettynä  ,
ts. merkitään
,
ts. merkitään 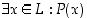 tai
tai 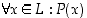 . Kummassakin tapauksessa avoimesta lauseesta on saatu kvanttorin lisäyksellä aikaan looginen lause, jolla on totuusarvo.
. Kummassakin tapauksessa avoimesta lauseesta on saatu kvanttorin lisäyksellä aikaan looginen lause, jolla on totuusarvo.
Esimerkki 1.3.1.
Lause 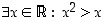 väittää, että on olemassa reaaliluku
väittää, että on olemassa reaaliluku 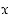 ,
jolle epäyhtälö
,
jolle epäyhtälö 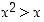 pätee. Se on tosi lause, sillä esimerkiksi luku
pätee. Se on tosi lause, sillä esimerkiksi luku 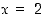 kelpaa etsityksi luvuksi. Monet muutkin luvut kelpaavat, mutta olemassaoloväitteen todeksi osoittamiseen riittää löytää yksi.
kelpaa etsityksi luvuksi. Monet muutkin luvut kelpaavat, mutta olemassaoloväitteen todeksi osoittamiseen riittää löytää yksi.
Myös lause 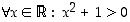 on tosi, sillä reaalilukujen neliöt ovat aina ei-negatiivisia, joten
on tosi, sillä reaalilukujen neliöt ovat aina ei-negatiivisia, joten 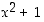 on aina positiivinen.
on aina positiivinen.

Usein vastaan saattaa tulla tilanne, jossa kvanttorilauseelle on tarpeen muodostaa negaatiolause. Seuraava antaa siihen muodollisen ratkaisun.
Lause 1.3.2. Lause (Negaation ja kvanttorin vaihtosääntö)
Avoimelle lauseelle 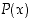 seuraavat ovat tautologioita:
seuraavat ovat tautologioita:
 ,
,
 .
.
Sanallisesti ilmaistuna edellinen tarkoittaa, että lauseen "jokaiselle luokan 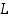 alkiolle
alkiolle 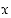 on
on 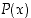 voimassa" vastaväite kuuluu "luokassa
voimassa" vastaväite kuuluu "luokassa 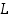 on alkio
on alkio 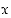 ,
jolle
,
jolle 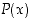 ei päde." Lausu mielessäsi vastaavasti toinen vaihtosääntö. Koska jokaiselle lauseelle joko se itse tai sitten sen negaatio on tosi, pätee esimerkiksi lauseista
ei päde." Lausu mielessäsi vastaavasti toinen vaihtosääntö. Koska jokaiselle lauseelle joko se itse tai sitten sen negaatio on tosi, pätee esimerkiksi lauseista 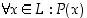 ja
ja 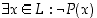 jokaisessa tilanteessa vain toinen.
jokaisessa tilanteessa vain toinen.
Esimerkki 1.3.3.
Reaaliluvusta 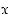 riippuvan lauseen
riippuvan lauseen 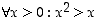 vastaväite on vaihtosäännön mukaan
vastaväite on vaihtosäännön mukaan 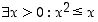 . Näistä siis vain toinen on tosi − jälkimmäinen, sillä esimerkiksi luku
. Näistä siis vain toinen on tosi − jälkimmäinen, sillä esimerkiksi luku 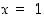 toteuttaa väitteen.
toteuttaa väitteen.

Kvanttoreita voidaan yhdistellä sellaisiksi lauseiksi, jotka riippuvat useammista muuttujista. Esimerkiksi kvanttorilause 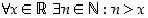 tarkoittaa, että "jokaista reaalilukua
tarkoittaa, että "jokaista reaalilukua
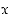 kohti on olemassa luonnollinen luku
kohti on olemassa luonnollinen luku 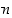 siten, että
siten, että 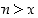 ", ja on siis tosi lause. Tässä
", ja on siis tosi lause. Tässä 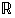 on reaalilukujen ja
on reaalilukujen ja 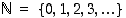 on luonnollisten lukujen joukko.
on luonnollisten lukujen joukko.
Perättäiset kvanttorit yhdistetään vasemmalta oikealle. Yllä oleva väite on siten muotoa 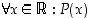 ,
missä
,
missä 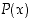 on luonnollisesta luvusta
on luonnollisesta luvusta 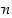 riippuva väite
riippuva väite 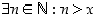 .
.
Myös väite 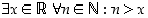 eli "on olemassa reaaliluku
eli "on olemassa reaaliluku 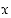 ,
jolle kaikilla luonnollisilla luvuilla
,
jolle kaikilla luonnollisilla luvuilla 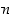 pätee
pätee 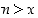 " on tosi lause, sillä luvuksi
" on tosi lause, sillä luvuksi 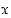 kelpaa mikä tahansa negatiivinen luku.
kelpaa mikä tahansa negatiivinen luku.
Opiskelutehtävä 5. (Kvanttorilauseiden totuusarvo)
Seuraavissa väitteissä kaikki muuttujat voivat olla nollasta eroavia kokonaislukuja. Määrää kunkin väitelauseen totuusarvo. Jos se on epätosi, muodosta myös lauseen negaatio.
(a) 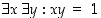 ,
,
(b) 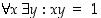 ,
,
(c) 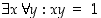 .
.
Vinkki tehtävään 5
Opiskelutehtävä 6. Kvanttorilauseen vastaväite)
Muodosta väitelauseen 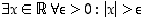 vastaväite ja mieti, kumpi väite pitää paikkansa. (
vastaväite ja mieti, kumpi väite pitää paikkansa. ( 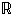 on reaalilukujen joukko.)
on reaalilukujen joukko.)
Vinkki tehtävään 6
Lopputoteamus: Loogisten operaatioiden ja symbolien hallinta ei ole tämän osan pääasia, vaan tarkoitus on tuoda esiin matemaattisen ajattelun perusperiaatteita ja korostaa täsmällisyyden merkitystä. Vältä kuitenkin liiallista lyhenteiden ja symbolien käyttöä. Pyri käyttämään sanallisempia ilmaisuja − ne hallitset automaattisesti paremmin. Jo muutamien sidesanojen käyttö ("jos …, niin …", "siten, että", "tästä/näistä seuraa …") tuo selkeyttä ja luettavuutta esitykseen.
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
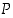 riippuu jostain muuttujasta
riippuu jostain muuttujasta 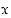 ,
ilmoitamme riippuvuuden kirjoittamalla
,
ilmoitamme riippuvuuden kirjoittamalla 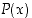 ja sanomme, että se on
avoin lause. Esimerkiksi
ja sanomme, että se on
avoin lause. Esimerkiksi 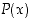 voi olla kokonaisluvusta
voi olla kokonaisluvusta 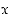 riippuva lause "
riippuva lause "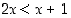 ". Jos tässä muuttujalle
". Jos tässä muuttujalle 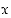 annetaan jokin arvo, avoin lause
annetaan jokin arvo, avoin lause 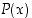 muuttuu lauseeksi, jolla on jokin totuusarvo, joko tosi tai epätosi.
muuttuu lauseeksi, jolla on jokin totuusarvo, joko tosi tai epätosi. 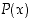 voi siis saada kumpiakin totuusarvoja, ts. voi olla olemassa arvo
voi siis saada kumpiakin totuusarvoja, ts. voi olla olemassa arvo 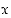 ,
jolle
,
jolle 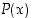 on tosi, ja voi olla olemassa arvo
on tosi, ja voi olla olemassa arvo 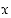 ,
jolle
,
jolle 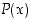 on epätosi. Tällainen on edellä mainittu lause "
on epätosi. Tällainen on edellä mainittu lause "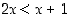 ".
". 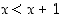 " on sellainen. Vastaavasti lause "
" on sellainen. Vastaavasti lause "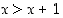 " on aina epätosi.
" on aina epätosi. 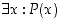 ,
kun tarkoitetaan, että on olemassa
,
kun tarkoitetaan, että on olemassa 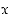 ,
jolla on ominaisuus
,
jolla on ominaisuus 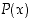 . Vastaavasti merkintä
. Vastaavasti merkintä 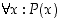 tarkoittaa, että kaikilla
tarkoittaa, että kaikilla 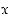 on ominaisuus
on ominaisuus 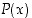 . Jos näissä lausumissa muuttuja
. Jos näissä lausumissa muuttuja 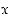 halutaan rajata johonkin joukkoon tai luokkaan
halutaan rajata johonkin joukkoon tai luokkaan 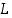 ,
merkitään silloin täsmennettynä
,
merkitään silloin täsmennettynä  ,
ts. merkitään
,
ts. merkitään 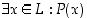 tai
tai 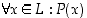 . Kummassakin tapauksessa avoimesta lauseesta on saatu kvanttorin lisäyksellä aikaan looginen lause, jolla on totuusarvo.
. Kummassakin tapauksessa avoimesta lauseesta on saatu kvanttorin lisäyksellä aikaan looginen lause, jolla on totuusarvo. 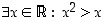 väittää, että on olemassa reaaliluku
väittää, että on olemassa reaaliluku 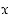 ,
jolle epäyhtälö
,
jolle epäyhtälö 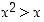 pätee. Se on tosi lause, sillä esimerkiksi luku
pätee. Se on tosi lause, sillä esimerkiksi luku 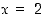 kelpaa etsityksi luvuksi. Monet muutkin luvut kelpaavat, mutta olemassaoloväitteen todeksi osoittamiseen riittää löytää yksi.
kelpaa etsityksi luvuksi. Monet muutkin luvut kelpaavat, mutta olemassaoloväitteen todeksi osoittamiseen riittää löytää yksi. 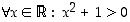 on tosi, sillä reaalilukujen neliöt ovat aina ei-negatiivisia, joten
on tosi, sillä reaalilukujen neliöt ovat aina ei-negatiivisia, joten 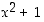 on aina positiivinen.
on aina positiivinen. 
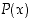 seuraavat ovat tautologioita:
seuraavat ovat tautologioita: ,
,
 .
. 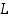 alkiolle
alkiolle 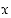 on
on 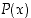 voimassa" vastaväite kuuluu "luokassa
voimassa" vastaväite kuuluu "luokassa 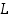 on alkio
on alkio 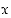 ,
jolle
,
jolle 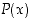 ei päde." Lausu mielessäsi vastaavasti toinen vaihtosääntö. Koska jokaiselle lauseelle joko se itse tai sitten sen negaatio on tosi, pätee esimerkiksi lauseista
ei päde." Lausu mielessäsi vastaavasti toinen vaihtosääntö. Koska jokaiselle lauseelle joko se itse tai sitten sen negaatio on tosi, pätee esimerkiksi lauseista 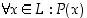 ja
ja 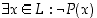 jokaisessa tilanteessa vain toinen.
jokaisessa tilanteessa vain toinen. 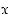 riippuvan lauseen
riippuvan lauseen 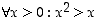 vastaväite on vaihtosäännön mukaan
vastaväite on vaihtosäännön mukaan 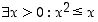 . Näistä siis vain toinen on tosi − jälkimmäinen, sillä esimerkiksi luku
. Näistä siis vain toinen on tosi − jälkimmäinen, sillä esimerkiksi luku 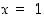 toteuttaa väitteen.
toteuttaa väitteen. 
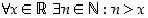 tarkoittaa, että "jokaista reaalilukua
tarkoittaa, että "jokaista reaalilukua
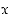 kohti on olemassa luonnollinen luku
kohti on olemassa luonnollinen luku 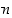 siten, että
siten, että 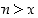 ", ja on siis tosi lause. Tässä
", ja on siis tosi lause. Tässä 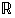 on reaalilukujen ja
on reaalilukujen ja 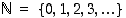 on luonnollisten lukujen joukko.
on luonnollisten lukujen joukko. 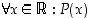 ,
missä
,
missä 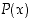 on luonnollisesta luvusta
on luonnollisesta luvusta 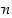 riippuva väite
riippuva väite 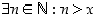 .
. 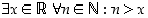 eli "on olemassa reaaliluku
eli "on olemassa reaaliluku 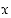 ,
jolle kaikilla luonnollisilla luvuilla
,
jolle kaikilla luonnollisilla luvuilla 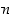 pätee
pätee 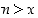 " on tosi lause, sillä luvuksi
" on tosi lause, sillä luvuksi 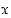 kelpaa mikä tahansa negatiivinen luku.
kelpaa mikä tahansa negatiivinen luku. 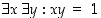 ,
,
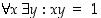 ,
,
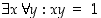 .
. 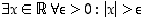 vastaväite ja mieti, kumpi väite pitää paikkansa. (
vastaväite ja mieti, kumpi väite pitää paikkansa. ( 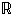 on reaalilukujen joukko.)
on reaalilukujen joukko.) 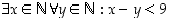 sanallisesti ja muodosta sen vastaväite symbolein ja sanallisesti. Kumpi väite pitää paikkansa? (
sanallisesti ja muodosta sen vastaväite symbolein ja sanallisesti. Kumpi väite pitää paikkansa? ( 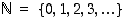 on luonnollisten lukujen joukko.)
on luonnollisten lukujen joukko.) 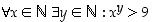 vastaväite symbolein ja sanallisesti. Kumpi väite pitää paikkansa?
vastaväite symbolein ja sanallisesti. Kumpi väite pitää paikkansa?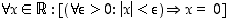 vastaväite ja mieti, kumpi näistä väitteistä pitää paikkansa. (
vastaväite ja mieti, kumpi näistä väitteistä pitää paikkansa. ( 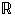 on reaalilukujen joukko.)
on reaalilukujen joukko.)