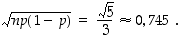VI.5. Jakauma ja odotusarvo
Olkoon 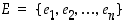 äärellisen todennäköisyyskentän perusjoukko.
Satunnaismuuttujaksi sanotaan yleisesti mitä tahansa satunnaisilmiöön liittyvää funktiota
äärellisen todennäköisyyskentän perusjoukko.
Satunnaismuuttujaksi sanotaan yleisesti mitä tahansa satunnaisilmiöön liittyvää funktiota 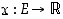 . Nopanheitossa se voi olla sama kuin tuloksena oleva silmäluku, kun taas lapsen sukupuolen määräytymisessä voidaan asettaa esimerkiksi, että
. Nopanheitossa se voi olla sama kuin tuloksena oleva silmäluku, kun taas lapsen sukupuolen määräytymisessä voidaan asettaa esimerkiksi, että 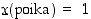 ja
ja 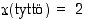 .
.
Satunnaismuuttujan yhteydessä merkinnällä 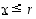 ,
missä
,
missä 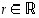 ,
tarkoitetaan tapahtumaa
,
tarkoitetaan tapahtumaa 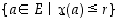 . Tämän avulla määritellään ns.
kertymäfunktio
. Tämän avulla määritellään ns.
kertymäfunktio 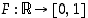 ,
jolle
,
jolle 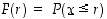 . Äärelliseen todennäköisyyskenttään liittyvän kertymäfunktion kuvaaja on aina portaittain kasvava. Se saa arvonlisäyksen
. Äärelliseen todennäköisyyskenttään liittyvän kertymäfunktion kuvaaja on aina portaittain kasvava. Se saa arvonlisäyksen 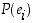 kohdissa
kohdissa 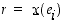 ja on näitten välillä vakiosuuruinen.
ja on näitten välillä vakiosuuruinen.
Satunnaismuuttujan 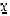 tiheysfunktiolla eli
frekvenssifunktiolla taas tarkoitetaan kuvausta
tiheysfunktiolla eli
frekvenssifunktiolla taas tarkoitetaan kuvausta 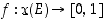 ,
jolle
,
jolle 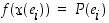 . Tiheysfunktion saamista arvoista eli alkeistapausten todennäköisyyksistä muodostuu satunnaismuuttujan
jakauma. Sitä sanotaan myös satunnaisilmiön
todennäköisyysjakaumaksi.
. Tiheysfunktion saamista arvoista eli alkeistapausten todennäköisyyksistä muodostuu satunnaismuuttujan
jakauma. Sitä sanotaan myös satunnaisilmiön
todennäköisyysjakaumaksi.
Esimerkki 6.5.1.
Nopanheitossa perusjoukkona on 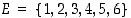 ja satunnaismuuttujalle voidaan asettaa, että
ja satunnaismuuttujalle voidaan asettaa, että 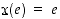 joukossa
joukossa 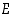 . Tiheysfunktio
. Tiheysfunktio 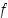 saa aina arvon
saa aina arvon 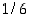 ja kertymäfunktiolle
ja kertymäfunktiolle 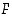 on
on
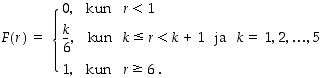
Kertymäfunktion kuvaaja on porrasfunktio. Piirrä tiheys- ja kertymäfunktion kuvaajat.

Esimerkki 6.5.2.
Heitettäessä noppaa neljästi olkoon 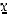 saatujen kuutosten lukumäärä. Tiheysfunktio
saatujen kuutosten lukumäärä. Tiheysfunktio 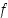 saa silloin binomitodennäköisyyden mukaan arvot
saa silloin binomitodennäköisyyden mukaan arvot
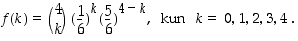
Taulukoidaan tiheysfunktion 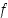 ja kertymäfunktion
ja kertymäfunktion 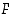 arvot näissä pisteissä:
arvot näissä pisteissä:
Alla ovat vielä tiheys- ja kertymäfunktioiden kuvaajat. Kertymäfunktion arvo kokonaislukupisteissä on ylemmällä tasolla oleva arvo.

Satunnaismuuttujan jakaumaan liittyy pari sen reaaliakselille sijoittumista kuvaavaa tunnuslukua, nimittäin odotusarvo ja keskihajonta. Satunnaismuuttujan
odotusarvo 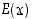 on sen todennäköisyyksillä painotettu keskiarvo, ts.
on sen todennäköisyyksillä painotettu keskiarvo, ts.
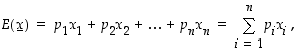
kun 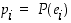 ja
ja 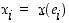 . Jakauman hajaantumista kuvaa taas
keskihajonta
. Jakauman hajaantumista kuvaa taas
keskihajonta
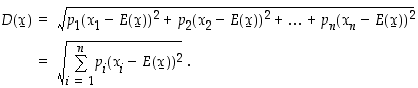
Esimerkki 6.5.3.
Nopanheitossa silmäluvun ilmoittavan satunnaismuuttujan odotusarvo on
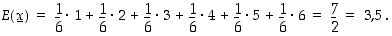
Tässä tapauksessa odotusarvo ei ole ollenkaan mahdollinen tulos. Odotusarvo ei siten välttämättä ole odotettavissa oleva arvo.
Nopanheitossa keskihajonnan neliö on
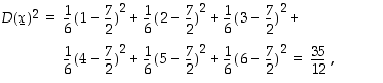
joten keskihajonta on
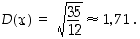

Esimerkki 6.5.4.
Heitettäessä noppaa neljästi olkoon 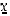 saatujen kuutosten lukumäärä. Tiheysfunktion
saatujen kuutosten lukumäärä. Tiheysfunktion 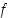 arvot on taulukoitu esimerkissä 6.5.2. Odotusarvoksi saadaan siten
arvot on taulukoitu esimerkissä 6.5.2. Odotusarvoksi saadaan siten
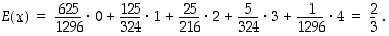

Yleisesti toistokokeeseen liittyvän binomijakauman odotusarvo on 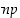 ja keskihajonta
ja keskihajonta 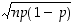 ,
kun
,
kun 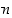 on toistojen lukumäärä ja
on toistojen lukumäärä ja 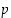 on tarkasteltavan tapahtuman onnistumistodennäköisyys. Todistus sivuutetaan tässä.
on tarkasteltavan tapahtuman onnistumistodennäköisyys. Todistus sivuutetaan tässä.
Esimerkki 6.5.5.
Edellisen tehtävän nopanheitossa on kyse binomijakaumasta, jossa 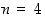 ja
ja 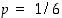 . Odotusarvoksi saadaan siten
. Odotusarvoksi saadaan siten 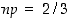 ja keskihajonnaksi
ja keskihajonnaksi
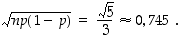

Harjoitustehtäviä
1. Laatikosta, jossa on 6 valkoista ja 10 mustaa palloa, nostetaan umpimähkään 5 palloa. Määrää sen satunnaismuuttujan odotusarvo, joka ilmoittaa nostettujen valkoisten pallojen määrän. Tarvittavat todennäköisyydet ovat laskettavana pykälän Otanta ja toistokoe tehtävässä 1. Piirrä myös tiheys- ja kertymäfunktioiden kuvaajat.
2. Tee edellinen tehtävä ( 6 valkoisen ja 10 mustan pallon joukosta nostetaan umpimähkään 5 palloa) sillä muutoksella, että pallot pannaan joka noston jälkeen takaisin laatikkoon. Tarvittavat todennäköisyydet ovat laskettavana pykälän Otanta ja toistokoe tehtävässä 2.
3. Arpajaisissa on myytävänä 300 kahden euron hintaista arpaa. Päävoittona on 100 euroa, toisena voittona 40 euroa ja kolmantena 20 euroa. Muita voittoja ei ole. Laske yhdellä arvalla saatavan voiton odotusarvo.
4. Tarkastele pykälän Ehdollinen todennäköisyys tehtävän 8 hajamielisen herran sateenvarjon unohtamisilmiötä. Määrää sen satunnaismuuttujan odotusarvo, joka ilmoittaa sen, kuinka monenteen kauppaan sateenvarjo on unohtunut. Piirrä myös tiheys- ja kertymäfunktioiden kuvaajat.
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
 äärellisen todennäköisyyskentän perusjoukko.
Satunnaismuuttujaksi sanotaan yleisesti mitä tahansa satunnaisilmiöön liittyvää funktiota
äärellisen todennäköisyyskentän perusjoukko.
Satunnaismuuttujaksi sanotaan yleisesti mitä tahansa satunnaisilmiöön liittyvää funktiota 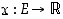 . Nopanheitossa se voi olla sama kuin tuloksena oleva silmäluku, kun taas lapsen sukupuolen määräytymisessä voidaan asettaa esimerkiksi, että
. Nopanheitossa se voi olla sama kuin tuloksena oleva silmäluku, kun taas lapsen sukupuolen määräytymisessä voidaan asettaa esimerkiksi, että 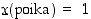 ja
ja 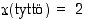 .
. 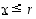 ,
missä
,
missä 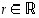 ,
tarkoitetaan tapahtumaa
,
tarkoitetaan tapahtumaa 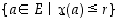 . Tämän avulla määritellään ns.
kertymäfunktio
. Tämän avulla määritellään ns.
kertymäfunktio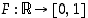 ,
jolle
,
jolle 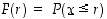 . Äärelliseen todennäköisyyskenttään liittyvän kertymäfunktion kuvaaja on aina portaittain kasvava. Se saa arvonlisäyksen
. Äärelliseen todennäköisyyskenttään liittyvän kertymäfunktion kuvaaja on aina portaittain kasvava. Se saa arvonlisäyksen 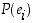 kohdissa
kohdissa 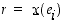 ja on näitten välillä vakiosuuruinen.
ja on näitten välillä vakiosuuruinen. 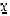 tiheysfunktiolla
tiheysfunktiolla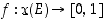 ,
jolle
,
jolle 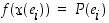 . Tiheysfunktion saamista arvoista eli alkeistapausten todennäköisyyksistä muodostuu satunnaismuuttujan
jakauma
. Tiheysfunktion saamista arvoista eli alkeistapausten todennäköisyyksistä muodostuu satunnaismuuttujan
jakauma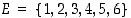 ja satunnaismuuttujalle voidaan asettaa, että
ja satunnaismuuttujalle voidaan asettaa, että 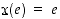 joukossa
joukossa 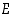 . Tiheysfunktio
. Tiheysfunktio 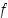 saa aina arvon
saa aina arvon 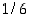 ja kertymäfunktiolle
ja kertymäfunktiolle 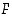 on
on 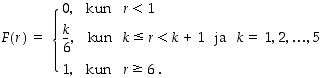

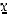 saatujen kuutosten lukumäärä. Tiheysfunktio
saatujen kuutosten lukumäärä. Tiheysfunktio 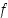 saa silloin binomitodennäköisyyden mukaan arvot
saa silloin binomitodennäköisyyden mukaan arvot 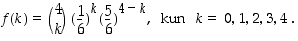
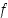 ja kertymäfunktion
ja kertymäfunktion 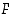 arvot näissä pisteissä:
arvot näissä pisteissä: 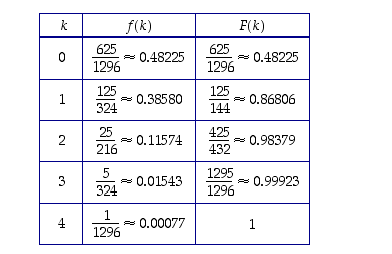
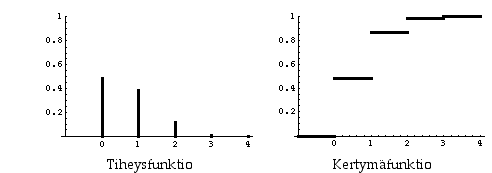

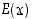 on sen todennäköisyyksillä painotettu keskiarvo, ts.
on sen todennäköisyyksillä painotettu keskiarvo, ts. 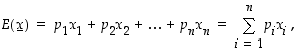
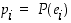 ja
ja 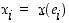 . Jakauman hajaantumista kuvaa taas
keskihajonta
. Jakauman hajaantumista kuvaa taas
keskihajonta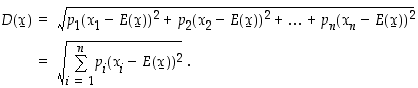
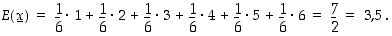
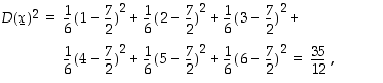
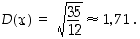

 saatujen kuutosten lukumäärä. Tiheysfunktion
saatujen kuutosten lukumäärä. Tiheysfunktion 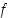 arvot on taulukoitu esimerkissä
arvot on taulukoitu esimerkissä 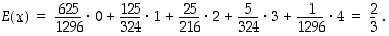

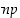 ja keskihajonta
ja keskihajonta 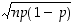 ,
kun
,
kun 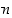 on toistojen lukumäärä ja
on toistojen lukumäärä ja 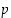 on tarkasteltavan tapahtuman onnistumistodennäköisyys. Todistus sivuutetaan tässä.
on tarkasteltavan tapahtuman onnistumistodennäköisyys. Todistus sivuutetaan tässä. 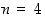 ja
ja 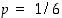 . Odotusarvoksi saadaan siten
. Odotusarvoksi saadaan siten 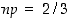 ja keskihajonnaksi
ja keskihajonnaksi