VI.4. Ehdollinen todennäköisyys
Oletetaan, että todennäköisyyskentässä 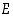 tapahtumalla
tapahtumalla 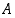 on positiivinen todennäköisyys,
on positiivinen todennäköisyys, 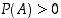 . Tarkastellaan jonkin toisen tapahtuman
. Tarkastellaan jonkin toisen tapahtuman 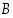 todennäköisyyttä sillä ehdolla, että tapahtuma
todennäköisyyttä sillä ehdolla, että tapahtuma 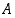 sattuu myös. Kyseessä on siten tapahtuman
sattuu myös. Kyseessä on siten tapahtuman 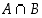 osuus tapahtumasta
osuus tapahtumasta 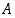 . Tämän perusteella ns. tapahtuman
. Tämän perusteella ns. tapahtuman 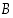 ehdollinen
todennäköisyys ehdolla
ehdollinen
todennäköisyys ehdolla 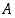 voidaan määritellä suhteella
voidaan määritellä suhteella
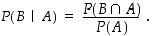
Ehdollinen todennäköisyys on todellakin uusi todennäköisyys perusjoukossa 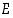 ,
sillä on varsin helppo todeta, että
,
sillä on varsin helppo todeta, että
(T1) 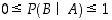 ,
,
(T2) 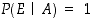 ,
ja
,
ja
(T3) jos 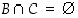 ,
niin
,
niin 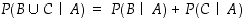 .
.
Esimerkki 6.4.1.
Korttipakasta vedetään kaksi korttia. Mikä on todennäköisyys, että toinen on ässä, kun ensimmäinen oli jo ässä?
Ratkaisua varten otetaan käyttöön tapahtumat 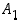 = "ensimmäinen kortti on ässä" ja
= "ensimmäinen kortti on ässä" ja 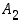 = "toinen kortti on ässä". Silloin
= "toinen kortti on ässä". Silloin
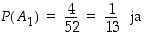
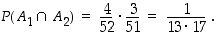
Siten kysytty todennäköisyys on
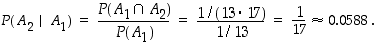
Toki tämä todennäköisyys voidaan laskea suoraankin, kun ajatellaan, että yhden ässän poisottamisen jälkeen pakassa on 51 korttia, joista kolme on ässää:
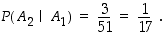

Tehtävä. Millä todennäköisyydellä kahdella nopalla saadaan silmäluvuiksi yhteensä vähintään 10 sillä ehdolla, että ensimmäisellä saadaan viitonen?
Ehdollisen todennäköisyyden määrittelystä saadaan ns.
kertolaskusääntö
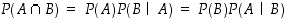 .
.
Kahden tapahtuman 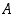 ja
ja 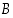 sanotaan olevan toisistaan (stokastisesti)
riippumattomia, jos
sanotaan olevan toisistaan (stokastisesti)
riippumattomia, jos 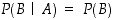 . Tällöin symmetrisesti myös
. Tällöin symmetrisesti myös 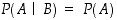 . Riippumattomille tapahtumillle kertolaskusääntö tulee yksinkertaisempaan muotoon
. Riippumattomille tapahtumillle kertolaskusääntö tulee yksinkertaisempaan muotoon
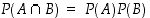 .
.
Huomaa, että riippumattomat tapahtumat eivät suinkaan ole erillisiä tapahtumia, vaan niiden suhteelliset osuudet toisistaan ovat samat kuin osuudet koko todennäköisyyskentässä.
Usein ehdollinen todennäköisyys voi olla helposti pääteltävissä ja silloin sitä voidaan käyttää kertolaskusäännön mukaisesti leikkaustapauksen 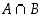 todennäköisyyden laskemiseen.
todennäköisyyden laskemiseen.
Esimerkki 6.4.2.
Korttipakka jaetaan tasan neljälle. Mikä on todennäköisyys, että pelaajat 1 ja 2 saavat kumpikin kaksi ässää?
Ratkaisua varten merkitään, että 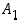 = "pelaaja 1 saa kaksi ässää" ja
= "pelaaja 1 saa kaksi ässää" ja 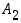 = "pelaaja 2 saa kaksi ässää". Silloin otantatodennäköisyyksien mukaisesti
= "pelaaja 2 saa kaksi ässää". Silloin otantatodennäköisyyksien mukaisesti
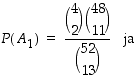
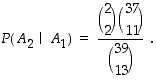
Tässä jälkimmäinen todennäköisyys saadaan ajattelemalla, että korttipakasta on jo otettu pois kolmetoista korttia, joista kaksi on ässää. Jäljellä on silloin kaksi ässää ja 37 muuta korttia.
Kysytty todennäköisyys on siten leikkaustapahtuman todennäköisyys
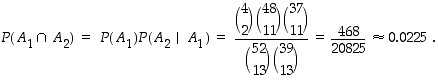

Kertolaskusääntöä voi käyttää myös toistuvasti kuten seuraavassa esimerkissä on tehty.
Esimerkki 6.4.3.
Mikä on todennäköisyys, että korttipakasta vedetään ensin hertta (
H), toiseksi risti (
R) ja kolmanneksi musta kortti (
M)?
Kysytään siis todennäköisyyttä 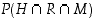 . Se saadaan kahden ehdollisen todennäköisyyden avulla seuraavasti. Ensinnäkin
. Se saadaan kahden ehdollisen todennäköisyyden avulla seuraavasti. Ensinnäkin
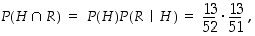
ja siten
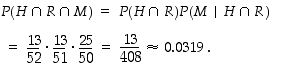

Opiskelutehtävä 62. (Ehdollinen todennäköisyys nopilla)
Noppaa heitetään kaksi kertaa. Millä todennäköisyydellä silmälukujen summa on vähintään 9 sillä ehdolla, että ainakin toisella heitoista saadaan silmäluku 5? Laske todennäköisyys sekä suoraan että käyttäen ehdollista todennäköisyyttä.
Vinkki tehtävään 62
Opiskelutehtävä 63. (Ehdollinen todennäköisyys korteilla)
Korttipakasta vedetään kolme korttia (ilman takaisinpanoa). Mikä on todennäköisyys, että ne ovat kaikki punaisia kuvakortteja? Laske todennäköisyys sekä suoraan että käyttäen ehdollista todennäköisyyttä.
Vinkki tehtävään 63
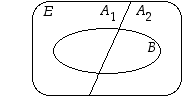
Tarkastellaan sitten tilannetta, jossa perusjoukko 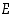 on jaettu kahteen erilliseen osaan
on jaettu kahteen erilliseen osaan 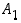 ja
ja 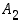 ,
jolloin
,
jolloin
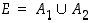 ,
,
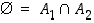 .
.
Tällaisessa tilanteessa sanotaan, että osajoukot 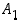 ja
ja  muodostavat joukon
muodostavat joukon 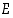 osituksen. Jos nyt
osituksen. Jos nyt 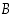 on jokin tapahtuma, muodostavat leikkausjoukot
on jokin tapahtuma, muodostavat leikkausjoukot 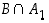 ja
ja 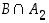 vuorostaan joukon
vuorostaan joukon 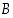 osituksen, ts.
osituksen, ts.
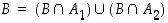 ja
ja 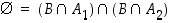 .
.
Siten aksiooman (T3) ja kertolaskusäännön perusteella saadaan, että
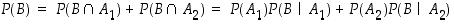 .
.
Tämä on ns.
kokonaistodennäköisyyden kaava ja se kuvaa satunnaisilmiön etenemistodennäköisyyttä tapahtumien 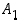 ja
ja 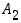 kautta tapahtumaan
kautta tapahtumaan 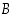
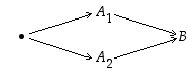 .
.
Yleistyksenä useammalle 'välitapahtumalle' saadaan, että jos
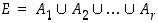
on perusjoukon 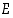 jako pistevieraisiin osiin eli se on joukon
jako pistevieraisiin osiin eli se on joukon 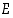 ositus,
pätee tapahtuman
ositus,
pätee tapahtuman 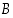 todennäköisyydelle, että
todennäköisyydelle, että
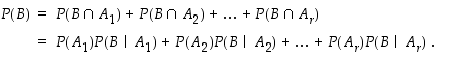
Esimerkki 6.4.4.
Kolmessa laatikossa on valkoisia ja mustia palloja seuraavasti:
Umpimähkään valitusta laatikosta nostetaan summassa yksi pallo. Millä todennäköisyydellä se on valkoinen?
Kun merkitään, että 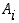 = "valitaan laatikko
i" (
= "valitaan laatikko
i" ( 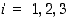 ) ja
) ja 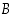 = "saadaan valkoinen pallo", saadaan kysytyksi kokonaistodennäköisyydeksi
= "saadaan valkoinen pallo", saadaan kysytyksi kokonaistodennäköisyydeksi
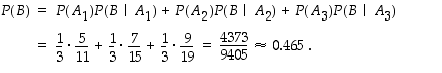

Opiskelutehtävä 64. (Kokonaistodennäköisyys)
Luvuista 1, …, 6 arvotaan yksi, olkoon se 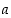 . Luvuista 1, …,
. Luvuista 1, …, 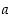 arvotaan sen jälkeen yksi. Mikä on todennäköisyys, että se on nelonen?
arvotaan sen jälkeen yksi. Mikä on todennäköisyys, että se on nelonen?
Vinkki tehtävään 64
Opiskelutehtävä 65. (Käänteinen todennäköisyys lapsilla)
Kaksilapsisesta perheestä tiedetään, että toinen lapsista on tytär. Millä todennäköisyydellä perheen toinen lapsi on poika? Jos lisäksi tiedetään, että toinen lapsi on nuorempi kuin em. tytär, mikä on silloin todennäköisyys, että hän on poika?
Vinkki tehtävään 65
Kun perusjoukko 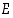 on jaettu kahtia, saadaan kokonaistodennäköisyyden kaavasta
on jaettu kahtia, saadaan kokonaistodennäköisyyden kaavasta
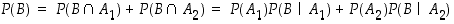
että esimerkiksi
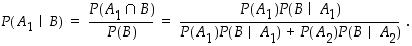
Tämä on ns.
käänteistodennäköisyys eli
Bayesin
kaava. Se vastaa siis kysymykseen, mikä on todennäköisyys, että tapahtuma 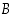 on sattunut tapahtuman
on sattunut tapahtuman 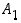 kautta. Vastaavasti määritellään käänteistodennäköisyys tapahtumalle
kautta. Vastaavasti määritellään käänteistodennäköisyys tapahtumalle 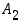 .
.
Kuten kokonaistodennäköisyyden kaava yleistyy käänteistodennäköisyyden kaava useammalle kuin kahdelle osajoukolle. Jos 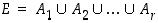 on perusjoukon
on perusjoukon 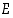 ositus,
niin
ositus,
niin
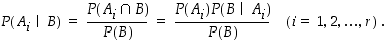
Esimerkki 6.4.5.
Oletetaan, että edellisen esimerkin 6.4.5 asetteluin nostetuksi palloksi on tullut valkoinen pallo. Mikä on todennäköisyys, että se oli nostettu ensimmäisestä laatikosta?
Nyt kysytään ehdollista todennäköisyyttä 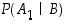 . Koska
. Koska
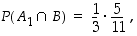
vastaus on
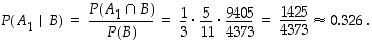
Samaan tapaan määrätään todennäköisyydet, että valittu pallo on tullut toisesta tai kolmannesta laatikosta:
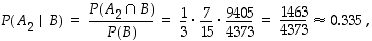
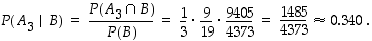
Huomaa, että laskettujen käänteistodennäköisyyksien summa on tasan yksi kuten pitääkin.

Opiskelutehtävä 66. (Käänteinen todennäköisyys tehdaskoneilla)
Tehtaassa on kaksi konetta, jotka valmistavat tiettyä tuotetta suhteessa 3:2. Edellinen kone tekee virheellisiä tuotteita todennäköisyydellä 0.01 ja jälkimmäinen todennäköisyydellä 0.02. Mikä on todennäköisyys, että virheelliseksi havaittu tuote on edellisen koneen tekemä? Entä jälkimmäisen?
Vinkki tehtävään 66
Harjoitustehtäviä
1. Noppaa heitetään kaksi kertaa. Millä todennäköisyydellä silmälukujen summa on vähintään 10 sillä ehdolla, että ainakin toisella heitoista saadaan silmäluku 5?
2. Olet heittänyt rahaa viisikymmentä kertaa ja saanut aina klaavan. Mikä on todennäköisyys, että seuraavalla kahdella heitolla saat kummallakin kruunan?
3. Luvuista 1, …, 6 arvotaan yksi, olkoon se 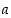 . Luvuista 1, …,
. Luvuista 1, …, 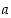 arvotaan taas yksi, olkoon se
arvotaan taas yksi, olkoon se 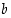 . Ja luvuista 1, …,
. Ja luvuista 1, …, 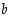 arvotaan vielä yksi. Mikä on todennäköisyys, että tämä kolmas luku on nelonen?
arvotaan vielä yksi. Mikä on todennäköisyys, että tämä kolmas luku on nelonen?
4. Korttipakasta vedetään umpimähkään kortteja. Mikä on todennäköisyys, että kuudennella vedolla saadaan kolmas pata?
5. Kahdesta samanlaisesta laatikosta tiedät vain, että toisessa on punainen ja toisessa valkoinen pallo. Lisäät valkoisen pallon toiseen laatikoista. Nostat tästä samasta laatikosta umpimähkään yhden pallon, joka osoittautuu valkoiseksi. Mikä on todennäköisyys, että siihen samaan laatikkoon jäi vielä valkoinen pallo?
6. Lääkäri tutkii potilaastaan erästä sairautta, joka esiintyy väestössä todennäköisyydellä 0.02. Hänellä on käytössään tutkimusmenetelmä, joka antaa positiivisen tuloksen (eli ilmaisee sairauden) todennäköisyydellä 0.90, mutta joka todennäköisyydellä 0.05 antaa virheellisesti positiivisen tuloksen, vaikka potilaalla ei kyseistä sairautta olisikaan. Jos menetelmä on antanut positiivisen tuloksen, mikä on todennäköisyys, että potilaalla on todella kyseinen sairaus. (Vihje: Laske ensin positiivisen tuloksen kokonaistodennäköisyys ja sitten kysytty ehdollinen todennäköisyys.) Jos tulos kummastuttaa, mieti, mitkä annetut todennäköisyydet sen aiheuttivat!
7. Oletetaan, että todennäköisyyskentässä 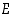 kummankin tapahtumista
kummankin tapahtumista 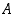 ja
ja 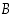 todennäköisyys on
todennäköisyys on 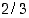 . Osoita (aksioomiin ja lauseisiin perustuen), että ehdollinen todennäköisyys
. Osoita (aksioomiin ja lauseisiin perustuen), että ehdollinen todennäköisyys 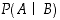 on vähintään puoli.
on vähintään puoli.
8. (a) Eräs hajamielinen herra unohtaa sateenvarjonsa kauppaan todennäköisyydellä 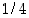 . Millä todennäköisyydellä hän on neljässä kaupassa käytyään unohtanut sateenvarjonsa?
. Millä todennäköisyydellä hän on neljässä kaupassa käytyään unohtanut sateenvarjonsa?
(b) Hajamielinen herra huomaa sitten neljässä kaupassa käytyään unohtaneensa sateenvarjonsa. Mikä on todennäköisyys, että sateenvarjo on jäänyt ensimmäiseen kauppaan? Entä toiseen, kolmanteen, tai neljänteen?
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
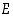 tapahtumalla
tapahtumalla 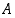 on positiivinen todennäköisyys,
on positiivinen todennäköisyys, 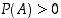 . Tarkastellaan jonkin toisen tapahtuman
. Tarkastellaan jonkin toisen tapahtuman 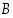 todennäköisyyttä sillä ehdolla, että tapahtuma
todennäköisyyttä sillä ehdolla, että tapahtuma 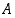 sattuu myös. Kyseessä on siten tapahtuman
sattuu myös. Kyseessä on siten tapahtuman 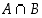 osuus tapahtumasta
osuus tapahtumasta 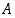 . Tämän perusteella ns. tapahtuman
. Tämän perusteella ns. tapahtuman 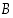 ehdollinen
todennäköisyys ehdolla
ehdollinen
todennäköisyys ehdolla 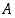 voidaan määritellä suhteella
voidaan määritellä suhteella 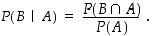
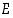 ,
sillä on varsin helppo todeta, että
,
sillä on varsin helppo todeta, että 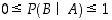 ,
,
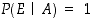 ,
ja
,
ja 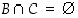 ,
niin
,
niin 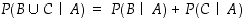 .
. 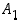 = "ensimmäinen kortti on ässä" ja
= "ensimmäinen kortti on ässä" ja 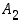 = "toinen kortti on ässä". Silloin
= "toinen kortti on ässä". Silloin 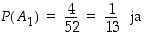
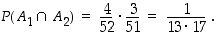
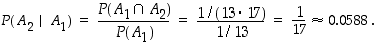
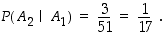

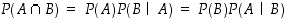 .
. 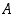 ja
ja 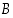 sanotaan olevan toisistaan (stokastisesti)
riippumattomia
sanotaan olevan toisistaan (stokastisesti)
riippumattomia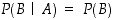 . Tällöin symmetrisesti myös
. Tällöin symmetrisesti myös 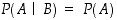 . Riippumattomille tapahtumillle kertolaskusääntö tulee yksinkertaisempaan muotoon
. Riippumattomille tapahtumillle kertolaskusääntö tulee yksinkertaisempaan muotoon 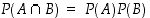 .
. 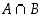 todennäköisyyden laskemiseen.
todennäköisyyden laskemiseen. 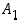 = "pelaaja 1 saa kaksi ässää" ja
= "pelaaja 1 saa kaksi ässää" ja 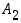 = "pelaaja 2 saa kaksi ässää". Silloin otantatodennäköisyyksien mukaisesti
= "pelaaja 2 saa kaksi ässää". Silloin otantatodennäköisyyksien mukaisesti 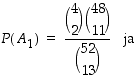
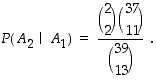
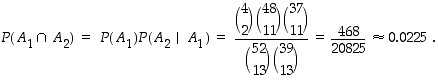

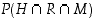 . Se saadaan kahden ehdollisen todennäköisyyden avulla seuraavasti. Ensinnäkin
. Se saadaan kahden ehdollisen todennäköisyyden avulla seuraavasti. Ensinnäkin 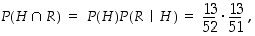
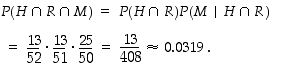

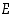 on jaettu kahteen erilliseen osaan
on jaettu kahteen erilliseen osaan 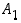 ja
ja 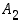 ,
jolloin
,
jolloin

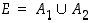 ,
,
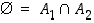 .
. 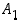 ja
ja  muodostavat joukon
muodostavat joukon 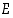 osituksen
osituksen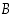 on jokin tapahtuma, muodostavat leikkausjoukot
on jokin tapahtuma, muodostavat leikkausjoukot 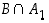 ja
ja 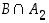 vuorostaan joukon
vuorostaan joukon 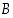
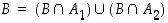 ja
ja 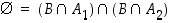 .
. 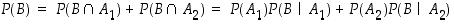 .
.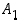 ja
ja 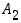 kautta tapahtumaan
kautta tapahtumaan 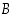
 .
. 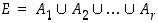
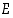 jako pistevieraisiin osiin eli se on joukon
jako pistevieraisiin osiin eli se on joukon 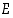
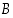 todennäköisyydelle, että
todennäköisyydelle, että 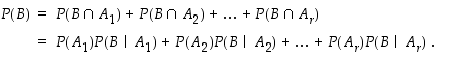

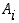 = "valitaan laatikko
i" (
= "valitaan laatikko
i" ( 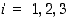 ) ja
) ja 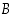 = "saadaan valkoinen pallo", saadaan kysytyksi kokonaistodennäköisyydeksi
= "saadaan valkoinen pallo", saadaan kysytyksi kokonaistodennäköisyydeksi 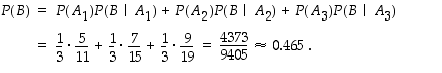

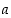 . Luvuista 1, …,
. Luvuista 1, …, 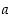 arvotaan sen jälkeen yksi. Mikä on todennäköisyys, että se on nelonen?
arvotaan sen jälkeen yksi. Mikä on todennäköisyys, että se on nelonen? 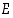 on jaettu kahtia, saadaan kokonaistodennäköisyyden kaavasta
on jaettu kahtia, saadaan kokonaistodennäköisyyden kaavasta 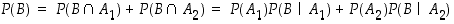
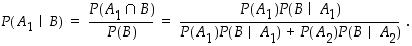
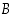 on sattunut tapahtuman
on sattunut tapahtuman 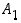 kautta. Vastaavasti määritellään käänteistodennäköisyys tapahtumalle
kautta. Vastaavasti määritellään käänteistodennäköisyys tapahtumalle 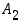 .
. 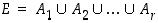 on perusjoukon
on perusjoukon 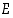
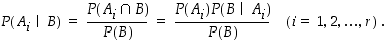
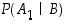 . Koska
. Koska 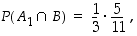
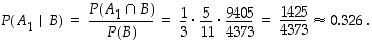
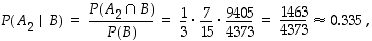
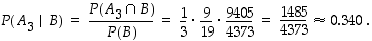

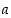 . Luvuista 1, …,
. Luvuista 1, …, 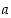 arvotaan taas yksi, olkoon se
arvotaan taas yksi, olkoon se 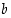 . Ja luvuista 1, …,
. Ja luvuista 1, …, 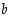 arvotaan vielä yksi. Mikä on todennäköisyys, että tämä kolmas luku on nelonen?
arvotaan vielä yksi. Mikä on todennäköisyys, että tämä kolmas luku on nelonen? 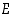 kummankin tapahtumista
kummankin tapahtumista 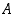 ja
ja 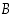 todennäköisyys on
todennäköisyys on 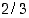 . Osoita (aksioomiin ja lauseisiin perustuen), että ehdollinen todennäköisyys
. Osoita (aksioomiin ja lauseisiin perustuen), että ehdollinen todennäköisyys 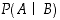 on vähintään puoli.
on vähintään puoli. 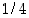 . Millä todennäköisyydellä hän on neljässä kaupassa käytyään unohtanut sateenvarjonsa?
. Millä todennäköisyydellä hän on neljässä kaupassa käytyään unohtanut sateenvarjonsa?