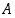todennäköisyys on 
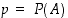. Toistetaan koetta ja lasketaan tapahtuman 
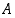esiintymiskerrat yhteen. Mikä on todennäköisyys, että tapahtuma 
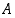esiintyy tietyn määrän verran?
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan vielä satunnaiskoetta, jossa jonkin yksittäisen tapahtuman 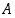todennäköisyys on 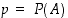. Toistetaan koetta ja lasketaan tapahtuman 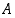esiintymiskerrat yhteen. Mikä on todennäköisyys, että tapahtuma 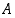esiintyy tietyn määrän verran?
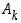= "tapahtuma 
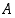sattuu täsmälleen 
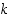kertaa" (
).
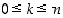Tulosäännön mukaan yhden koesarjan, jossa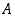 
sattuu 
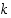kertaa ja ei satu 
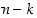kertaa, todennäköisyys on 
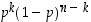. Tällaisia koesarjoja on 
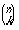erilaista, joten yhteenlaskien saadaan, että
Tätä todennäköisyyttä sanotaan
binomitodennäköisyydeksi. Se on sama kuin otantatodennäköisyys (ilman takaisinpanoa), kun siinä asetetaan, että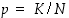 
. Binomikaavan mukaan näiden todennäköisyyksien summa on
Heitetään rahaa kuusi kertaa. Millä todennäköisyydellä saadaan a) täsmälleen neljä kruunua, b) vähintään neljä kruunua?
a) Oletetaan, että kruunun esiintymistodennäköisyys yksittäisessä heitossa on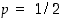 
. Koska nyt 
,
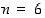on
b) Vähintään neljä kertaa kruunu esiintyy todennäköisyydellä
Tehtävä. Millä todennäköisyydellä täsmälleen puolet kymmenestä nastasta jää heitettäessä kärki ylöspäin, jos nasta jää kärki ylöspäin todennäköisyydellä 0.6? Entä ainakin yksi?
1. Laatikosta, jossa on 6 valkoista ja 10 mustaa palloa, nostetaan umpimähkään 5 palloa. Tee taulukko, josta näkyy kullekin nostettujen valkoisten pallojen määrälle sen todennäköisyys.
2. Tee edellinen tehtävä ( 6 valkoisen ja 10 mustan pallon joukosta nostetaan umpimähkään 5 palloa) sillä muutoksella, että pallot pannaan joka noston jälkeen takaisin laatikkoon. Tee taulukko, jossa näkyvät molempien tapojen todennäköisyydet (likiarvoina).
3. Säännöllistä tetraedriä, jonka kolme tahkoa on maalattu punaiseksi ja yksi valkoiseksi, heitetään kolme kertaa. Millä todennäköisyydellä joka kerta alin tahko on punainen? Määrää myös todennäköisyydet, että punainen tahko tulee alimmaksi kaksi kertaa, yhden kerran tai ei yhtään kertaa. (Tämä on sama kuin edellisen pykälän Äärellinen todennäköisyyskenttä harjoitustehtävä 2. Laske nyt kaikki binomitodennäköisyyksinä.)
4. Kukan siementen itämisprosentti on 70. Kuinka monta siementä on kylvettävä, että todennäköisyydellä 0.90 ainakin yksi siemen itäisi?
5. Kuinka monta opiskelijaa olisi luennolla oltava, että vähintään todennäköisyydellä puoli jollain heistä olisi syntymäpäivä luentopäivänä?
6. Oletetaan, että binäärisessä tiedonsiirtojärjestelmässä satunnaisten, toisistaan riippumattomien häiriöiden vuoksi nolla vääristyy ykköseksi todennäköisyydellä 0.01 ja ykkönen vääristyy nollaksi todennäköisyydellä 0.02. Mikä on todennäköisyys, että lähetetty sana 1001101 saapuu vastaanottimeen niin, että korkeintaan yksi merkki on virheellinen?
toistojen lukumäärä ja 
