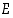Aksiomatisointi

Esitämme todennäköisyyden käsitteen tarkemman määrittelyn. Samalla yleistämme edellä olleen symmetristen alkeistapausten lukumäärään perustuvan määrittelyn. Olkoon sitä varten 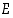äärellinen (perus)joukko. Merkitään sen kaikkien osajoukkojen eli kaikkien tapahtumien joukkoa

.

Sitä sanotaan joukon 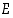potenssijoukoksi. Nimitys tulee siitä, että 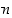−alkioiselle joukolle sen alkioiden lukumäärä on 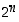, kuten edellä kombinaatioiden yhteydessä todettiin. Äärellinen todennäköisyyskenttä on nyt mikä tahansa kolmikko

,

missä 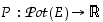on sellainen kuvaus, että kaikilla osajoukoilla 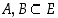pätee:

(T1)   ,

(T2)   ,

(T3)   jos , niin .

Luku 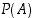on tapahtuman 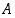todennäköisyys. Aksiooma (T3) on nimeltään erillisten tapahtumien yhteenlaskusääntö.

Seuraavassa on eräitä suoraan määrittelystä saatavia perusominaisuuksia. Nämä ovat siinä mielessä luonnollisen tuntuisia, että joukkojen alkioiden lukumääräsuhteelle 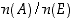pätevät kaikki nämä samat ominaisuudet.

Lause 6.2.4.

Äärellisen todennäköisyyskentän tapahtumalle 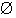("mahdoton tapaus") sekä tapahtumille 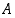ja 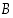pätevät:

(a)   ,

(b)   ,     Komplementtisääntö

(c)   ,

(d)   jos , niin ,     Monotonisuus

(e) 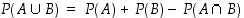  .    Yleinen yhteenlaskusääntö

Todistus. (a) Koska 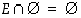, on aksiooman (T3) mukaan

eli , joten .

(b) Koska nyt 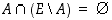, saadaan vastaavasti aksioomien (T3) ja (T2) perusteella päättelyketju:

(c) Tämän kohdan väite todennetaan vastaavasti kuin kohta (b), kunhan huomataan ensin, että

ja .

(d) Edellisen kohdan mukaan saadaan (tapahtumien 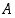ja 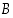roolit vaihtamalla), että

,

koskapa 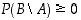aksiooman (T1) mukaan.

(e) Koska

ja ,

on aksiooman (T3) mukaan

,

mistä edelleen kohdan (c) mukaan saadaankin väite.

Opiskelutehtävä 57. (Leikkaustapahtuman todennäköisyys)

Tapahtuman 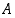todennäköisyys on 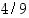ja tapahtuman 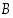todennäköisyys on 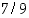. Voivatko tapahtumat 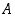ja 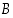olla erilliset? Määrää ala- ja ylärajat tapahtuman 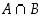todennäköisyydelle.

Vinkki tehtävään 57

Jos perusjoukon 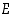alkiot luetellaan, esimerkiksi 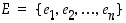, todennäköisyysfunktio 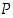voidaan määritellä myös ilmoittamalla alkeistapausten todennäköisyydet eli luvut 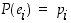. Näille on asetettava täsmälleen seuraavat ehdot:

(a)   kaikilla ,

(b)   .

Erityisesti on huomattava, että alkeistapausten ei tarvitse olla mitenkään symmetrisiä. Symmetrisessä kentässä on tietenkin .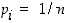

Esimerkki 6.2.5.

Lapsen sukupuoli voi olla tyttö (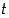) tai poika (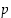). Voisi olettaa, että symmetrisesti 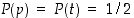. Kuitenkin suurista havaintoaineistoista on nähtävissä, että valinnat 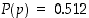ja 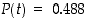vastaisivat paremmin todellisuutta. Kyseessä on silloin ns. tilastollinen todennäköisyys.

Esimerkki 6.2.6.

Tarkastellaan seuraavaa syntymäpäiväprobleemaa: Millä todennäköisyydellä kahdentoista henkilön ryhmässä on ainakin kahdella samana päivänä syntymäpäivä?

Oletetaan, että vuodessa on aina 365 päivää ja että kukin päivä on yhtä todennäköinen syntymäpäivä. Perusjoukko 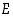muodostuu silloin päivämäärien 12−jonoista, jollainen on esimerkiksi jono (13.1., 15.12., 24.4., … , 29.4.). Näitä on kaikkiaan 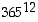erilaista jonoa.

Olkoon 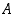tapahtuma "ainakin kahdella on sama syntymäpäivä". Koska tapahtuman 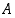alkeistapaukset ovat selvästi vaikeammin lueteltavissa kuin sen komplementtitapahtuman 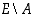= "kaikilla eri syntymäpäivä", siirrytäänkin komplementtitodennäköisyyden laskemiseen lauseen 6.2.4 kohdan (b) mukaisesti. Tulosäännön mukaan on 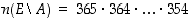ja siten

.

Yleisemmin voidaan yllä olevaan tapaan päätellä, että jos ryhmässä on 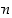henkilöä, on ainakin kahdella sama syntymäpäivä todennäköisyydellä

.

Seuraavassa on joitakin merkittäviä arvoja laskettuna:

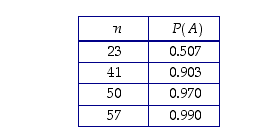
Esimerkki 6.2.7. (de Mérén probleema)

Kannattaako lyödä vetoa siitä, että heitettäessä neljä kertaa noppaa saadaan ainakin yksi kuutonen?

Käytetään tehtävän ratkaisuun symmetristä todennäköisyyskenttää, jossa alkeistapauksina ovat 4−jonot 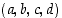, missä 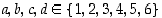. Perusjoukko 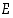on kaikista näistä jonoista muodostuva joukko ja siinä on siten 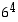alkiota. Jos nyt 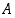on tapahtuma "saadaan ainakin yksi kuutonen", sen komplementtitapahtuma on "ei saada yhtään kuutosta" ja sille 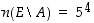. Siten

Kannattaa siis.

Esimerkki 6.2.8.

Laatikossa olkoon 12 lamppua, joista tiedetään, että 3 on viallista. Millä todennäköisyydellä laatikosta otetuissa kahdesta lampusta ainakin toinen on rikkinäinen?

Kuten esimerkissä 6.1.6 todettiin nostomahdollisuuksia on kaikkiaan

Jos 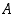on kyseinen tapahtuma, on 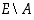= "molemmat lamput ovat ehjiä" ja sille

Siten kysytty todennäköisyys on

Opiskelutehtävä 58. (Vakioveikkauksen voittotodennäköisyys)

Vakioveikkauksessa on 13 kohdetta ja kunkin kohteen veikkausmahdollisuudet ovat 1, X ja 2. Mikä on todennäköisyys, että yhdellä veikkaussarakkeella saa täysosuman. Entä vähintään yksi oikein?

Vinkki tehtävään 58

Opiskelutehtävä 59. (Yhden kuutosen saaminen nopilla)

Kuinka monta kertaa on noppaa heitettävä, että saataisiin todennäköisyydellä 0.9 ainakin yksi kuutonen?

Vinkki tehtävään 59

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]