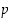 ja
ja 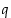 eri alkulukuja,
eri alkulukuja, 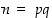 ja
ja 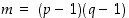 . Olkoon edelleen kokonaisluku
. Olkoon edelleen kokonaisluku 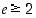 sellainen, että
sellainen, että 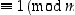 ,
ja kokonaisluku
,
ja kokonaisluku 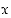 sellainen, että
sellainen, että 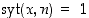 . Silloin pätee, että
. Silloin pätee, että 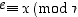 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Englantilaiset Rivest, Shamir ja Adleman julkaisivat vuonna 1978 erään suuriin alkulukuihin perustuvan salausmenetelmän, joka on osoittautunut tarpeeksi yksinkertaiseksi, mutta kuitenkin riittävän suojaavaksi. Menetelmää kutsutaan nykyään RSA-menetelmäksi. Se perustuu seuraavaan tulokseen.
Olkoot 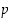 ja
ja 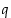 eri alkulukuja,
eri alkulukuja, 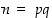 ja
ja 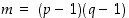 . Olkoon edelleen kokonaisluku
. Olkoon edelleen kokonaisluku 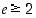 sellainen, että
sellainen, että 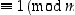 ,
ja kokonaisluku
,
ja kokonaisluku 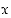 sellainen, että
sellainen, että 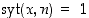 . Silloin pätee, että
. Silloin pätee, että 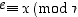 .
.
Todistus. (Jos todistus ei tunnu kiinnostavalta, hyppää sen yli! Todistuksen ideoita ei tarvita myöhemmin.) Oletuksen 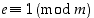 nojalla
nojalla 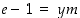 jollekin kokonaisluvulle
jollekin kokonaisluvulle 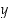 . Silloin
. Silloin
joten riittää osoittaa, että 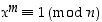 . Koska
. Koska 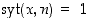 ,
luku
,
luku 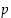 ei jaa lukua
ei jaa lukua 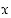 eli
eli 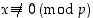 . Fermat'n pikkulause 3.4.6 ilmoittaa silloin, että
. Fermat'n pikkulause 3.4.6 ilmoittaa silloin, että
Vastaavasti symmetriasyistä 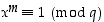 . Siten sekä
. Siten sekä 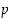 että
että 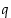 jakavat luvun
jakavat luvun 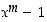 . Koska ne ovat eri alkulukuja, myös niiden tulo
. Koska ne ovat eri alkulukuja, myös niiden tulo 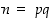 jakaa samaisen luvun. Siten on saatu, että
jakaa samaisen luvun. Siten on saatu, että 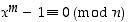 ,
mikä pitikin todistaa.
,
mikä pitikin todistaa.
Itse menetelmän kulku selvinnee parhaiten esimerkin avulla.
Esimerkki 3.5.2. (RSA-menetelmän algoritmi)
1° Koodin laatija valitsee kaksi (yleensä suurta) alkulukua, esimerkiksi
3° Laatija valitsee
koodausavaimen 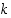 siten, että
siten, että 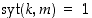 ,
esimerkiksi
,
esimerkiksi
4° Laatija laskee luvulle 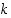 käänteisalkion
käänteisalkion 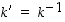 renkaassa
renkaassa 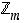 : Jakoyhtälön mukaisesti
: Jakoyhtälön mukaisesti 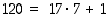 ,
joten
,
joten 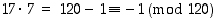 . Siten
. Siten 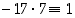 ja edelleen
ja edelleen 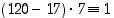 eli
eli 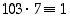 . Niinpä nyt
. Niinpä nyt
5° Laatija antaa viestin lähettäjälle tiedoksi vain luvut 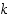 ja
ja 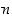 . Ja viestin vastaanottajalle vain luvut
. Ja viestin vastaanottajalle vain luvut 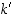 ja
ja 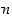 . Luku
. Luku 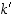 on ns.
purkuavain.
on ns.
purkuavain.
6° Lähettäjä lähettää sellaisen (numero)viestin 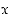 ,
jolle
,
jolle 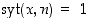 ,
koodattuna kaavalla
,
koodattuna kaavalla 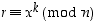 ; esimerkiksi viestille
; esimerkiksi viestille
Koska 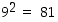 ja
ja 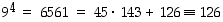 ,
koodatuksi viestiksi saadaan laskettua
,
koodatuksi viestiksi saadaan laskettua
7° Vastaanottaja purkaa koodatun viestin 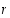 kaavalla
kaavalla 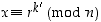 :
:
Tarkistetaan vielä, että purkutulos on oikein. Kun lasketaan modulo 143, saadaan ensinnä alkion 48 neliön neliöille jne:
Käyttäen potenssiluvun 103 binääriesitystä 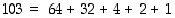 hyväksi saadaan siten, että
hyväksi saadaan siten, että
Miksi sitten viestin purku onnistuu aina? Jos merkitään, että 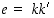 ,
on silloin
,
on silloin 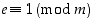 ja
ja 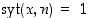 ,
joten edellä olevaa lausetta 3.5.1 voidaan käyttää. Sen mukaan
,
joten edellä olevaa lausetta 3.5.1 voidaan käyttää. Sen mukaan
Eräs RSA-menetelmän etu on se, että siinä viestin lähettäjä ja vastaanottaja käyttävät eri avaimia. Perinteisissä salausmenetelmissä he yleensä ovat käyttäneet samaa avainta. Pelkästään toisen avaimen avulla on myös lähes mahdotonta murtaa salausmenetelmää.
Edes koodauksen perustana olevan luvun 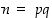 tietäminen ei anna heti murtomahdollisuutta. Tätä kuvannee hyvin internet-verkossa 1990-luvun alussa julkaistu koodattu viesti, jonka ilmoitettiin perustuvan annettuun 129−numeroiseen lukuun. Ensimmäisenä ratkaisun löytänyt ryhmä ilmoitti käyttäneensä viestin murtamiseen kahdeksan kuukautta ja noin 600 alilaskijaa 20 eri maassa. Yhteenlaskettuna tietokoneaikaa tarvittiin noin 5000 mips-vuotta (mips = miljoona toimintoa sekunnissa)!
tietäminen ei anna heti murtomahdollisuutta. Tätä kuvannee hyvin internet-verkossa 1990-luvun alussa julkaistu koodattu viesti, jonka ilmoitettiin perustuvan annettuun 129−numeroiseen lukuun. Ensimmäisenä ratkaisun löytänyt ryhmä ilmoitti käyttäneensä viestin murtamiseen kahdeksan kuukautta ja noin 600 alilaskijaa 20 eri maassa. Yhteenlaskettuna tietokoneaikaa tarvittiin noin 5000 mips-vuotta (mips = miljoona toimintoa sekunnissa)!
1. Olkoon RSA-menetelmässä 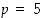 ja
ja 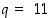 sekä koodausavain
sekä koodausavain 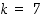 . Laske viestille
. Laske viestille 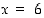 koodattu viesti.
koodattu viesti.
2. Määrää edellisen tehtävän tilanteessa purkuavain, pura koodattu viesti (41) ja tarkista, että tuloksena on alkuperäinen viesti.
3. Sinulle on annettu RSA-menetelmän käyttöä varten luku 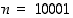 ja koodausavain
ja koodausavain 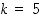 . Koodaa tämän perusteella numeroviestit 24 ja 53. Mikä on purkuavain?
. Koodaa tämän perusteella numeroviestit 24 ja 53. Mikä on purkuavain?