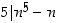ja b) 
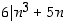voidaan modulolaskennan merkinnöin ilmoittaa yhtäpitävissä muodoissa a) 
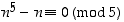ja b)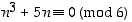 
. Todistetaan nämä:
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
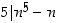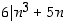Väitteet a) ja b) voidaan modulolaskennan merkinnöin ilmoittaa yhtäpitävissä muodoissa a) 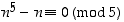ja b) 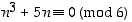. Todistetaan nämä:
a) Alla olevassa taulukossa kaikille ekvivalenssiluokkien edustajille (vasemman sarakkeen luvuille
n) on taulukoitu arvot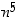 
ja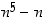 
modulo 5:
Koska tulos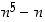 
on aina kongruentti nollan kanssa, niin väite pätee.
Väite pätee edellä olevan mukaan itse asiassa kaikille kokonaisluvuille, ei vain luonnollisille luvuille.
b) Perustelu taulukolla kuten edellä:
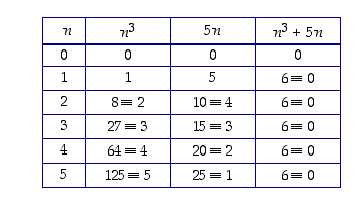
Lisätietoja. Vertaa tätä ratkaisua opiskelutehtävän 14 ratkaisuun, jossa tämän tehtävän väitteet on todistettu luonnollisille luvuille. Tämän tehtävän lähestymistapa kuitenkin toimii myös koko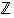 
:ssa.
[Opiskelutehtävä 29] [Vinkki tehtävään 29]