Summan integrointi
Funktioiden 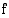 ja
ja 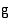 summan
summan 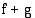 integraalifunktio on funktioiden
integraalifunktio on funktioiden 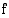 ja
ja 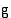 integraalifunktioiden summa:
integraalifunktioiden summa:
Derivoimissäännöistä voidaan johtaa seuraavat integroimissäännöt.
Funktioiden 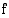 ja
ja 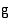 summan
summan 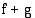 integraalifunktio on funktioiden
integraalifunktio on funktioiden 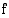 ja
ja 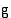 integraalifunktioiden summa:
integraalifunktioiden summa:
Funktion 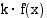 , missä
, missä 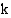 on jokin vakio, integraalifunktio saadaan, kun kerrotaan funktion
on jokin vakio, integraalifunktio saadaan, kun kerrotaan funktion 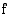 integraalifunktio vakiolla
integraalifunktio vakiolla 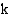 :
:
Potenssifunktion 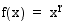 , missä
, missä 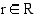 ja
ja 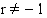 , integraalifunktio on
, integraalifunktio on
Määrää polynomifunktion 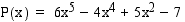 kaikki integraalifunktiot.
kaikki integraalifunktiot.
Integroinnin tuloksen voi aina tarkistaa derivoimalla:
Koska tulolle ei ole erityistä integroimissääntöä, suoritetaan ensin kertolasku ja integroidaan näin saatu funktio.
Edellä esitelty potenssifunktion integroimissääntö sopii kaikille niille potenssifunktioille 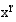 , joilla
, joilla 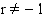 . Mikä sitten olisi funktion
. Mikä sitten olisi funktion 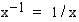 integraalifunktio? Koska luonnollisen logaritmifunktion derivoimissäännön mukaan
integraalifunktio? Koska luonnollisen logaritmifunktion derivoimissäännön mukaan 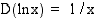 , kun
, kun 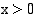 , on potenssifunktion
, on potenssifunktion 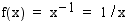 integraalifunktio
integraalifunktio
Logaritmifunktion argumentissa on itseisarvo, koska logaritmi on määritelty ainoastaan positiivisilla luvuilla. Derivoimalla on helppo todeta, että em. integroimissääntö on voimassa myös, kun 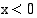 , jolloin sen itseisarvo on
, jolloin sen itseisarvo on 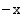 .
.
Osamäärälle ei ole olemassa erityistä integroimissääntöä. Jaetaan jokainen osoittajan termi erikseen nimittäjällä ja integroidaan näin saatu funktio.
Eksponenttifunktioiden derivoimissääntöjen nojalla niiden integraalifunktiot ovat:
Koska 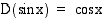 , on kosinifunktion integraalifunktio
, on kosinifunktion integraalifunktio
Yhdistetyn funktion derivoimissäännöistä voidaan johtaa lisää integroimissääntöjä, jotka on koottu seuraavaan luetteloon.
Edellä esitellyt integroimissäännöt sopivat vain tiettyihin funktioihin. Esimerkiksi funktion 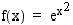 integrointi ei onnistu niiden avulla. Hankalissa tapauksissa kannattaa kokeilla osittaisintegrointia tai integrointia sijoituksen aulla. Tällä kurssilla nämä integrointimenetelmät sivuutetaan. Halutessaan lukija voi opiskella menetelmät sopivista integraalilaskentaa käsittelevistä oppikirjoista.
integrointi ei onnistu niiden avulla. Hankalissa tapauksissa kannattaa kokeilla osittaisintegrointia tai integrointia sijoituksen aulla. Tällä kurssilla nämä integrointimenetelmät sivuutetaan. Halutessaan lukija voi opiskella menetelmät sopivista integraalilaskentaa käsittelevistä oppikirjoista.
Kun kivi heitetään suoraan ylöspäin alkunopeudella 26 (m/s), sen nopeus 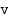 (m/s) ajan
(m/s) ajan 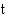 (s) funktiona on
(s) funktiona on
Muodosta funktio, joka ilmoittaa kiven korkeuden 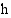 (m) lähtötasolta mitattuna. Kuinka kauan kivi on ilmassa?
(m) lähtötasolta mitattuna. Kuinka kauan kivi on ilmassa?
Kiven nopeus on sen sijainti- eli korkeusfunktion derivaatta. Kiven korkeusfunktio on jokin sen nopeusfunktion integraalifunktio.
Koska kiven korkeus hetkellä 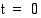 (s) on heittotason korkeus
(s) on heittotason korkeus 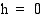 (m) ja
(m) ja 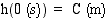 , edellä saaduista integraalifunktioista korkeuden ilmoittaa se, jossa vakio
, edellä saaduista integraalifunktioista korkeuden ilmoittaa se, jossa vakio 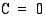 (m). Kiven korkeuden
(m). Kiven korkeuden 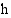 (m) ajan
(m) ajan 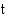 (s) kuluttua heitosta ilmoittaa funktio
(s) kuluttua heitosta ilmoittaa funktio
Kiven lentoaika saadaan, kun ratkaistaan yhtälö 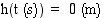 .
.
Vastaus: Kiven korkeus ajan funktiona on 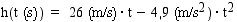 . Kivi on ilmassa n. 5,3 (s).
. Kivi on ilmassa n. 5,3 (s).
Erään hyödykkeen rajakustannukset 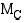 (mk/kpl) ovat tuotantonopeuden
(mk/kpl) ovat tuotantonopeuden 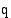 (kpl/kk) funktiona
(kpl/kk) funktiona
Muodosta funktio, joka ilmoittaa tuotantokustannukset 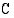 (mk/kk) tuotantonopeuden
(mk/kk) tuotantonopeuden 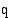 (kpl/kk) funktiona, kun kiinteät tuotantokustannukset ovat 1200 (mk/kk). Kuinka suuret ovat hyödykkeen tuotantokustannukset, kun tuotantonopeus on 1500 (kpl/kk)?
(kpl/kk) funktiona, kun kiinteät tuotantokustannukset ovat 1200 (mk/kk). Kuinka suuret ovat hyödykkeen tuotantokustannukset, kun tuotantonopeus on 1500 (kpl/kk)?
Hyödykkeen rajakustannukset ovat sen tuotantokustannusten muutosnopeus, joten rajakustannukset ovat tuotantokustannusten derivaattafunktio. Tuotantokustannusfunktio on siten eräs rajakustannusten integraalifunktio.
Kun 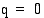 (kpl/kk), tuotantokustannukset ovat 1200 (mk/kk). Koska
(kpl/kk), tuotantokustannukset ovat 1200 (mk/kk). Koska
oheisista rajakustannusten integraalifunktioista tuotantokustannukset ilmoittaa se, jolla vakio 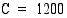 (mk/kk). Tuotantokustannukset ovat
(mk/kk). Tuotantokustannukset ovat
Kun tuotantonopeus on 1500 (kpl/kk), tuotantokustannukset ovat
Vastaus: Tuotantokustannukset tuotantonopeuden funktiona ovat
Kun tuotantonopeus on 1500 (kpl/kk), kustannukset ovat 41700 (mk/kk).
7. Raketin nopeus on lähdön jälkeen vähän aikaa suoraan verrannollinen lähtöhetkestä kuluneen ajan neliöön. Neljän sekunnin kuluttua lähdöstä raketin nopeus oli 62 (m/s). Kuinka pitkän matkan raketti kulki neljän ensimmäisen sekunnin aikana?
8. Erään kaupungin asukasluvun arvioidaan kasvavan 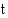 (kk):n kuluttua tästä hetkestä alkaen nopeudella
(kk):n kuluttua tästä hetkestä alkaen nopeudella
Kaupungin asukasluku on tällä hetkellä 12600 (as). Laske kaupungin arvioitu asukasluku 9 (kk):n kuluttua.
9. Erään hyödykkeen rajakustannukset 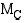 (mk/kpl) ovat tuotantonopeuden
(mk/kpl) ovat tuotantonopeuden 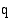 (kpl/kk) funktiona
(kpl/kk) funktiona 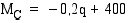 (mk/kpl). Mitkä ovat rajakustannusfunktion määrittelyssä esiintyvien vakioiden mittayksiköt? Kiinteät tuotantokustannukset ovat 9000 (mk/kk). Muodosta funktio, joka ilmoittaa hyödykkeen tuotantokustannukset
(mk/kpl). Mitkä ovat rajakustannusfunktion määrittelyssä esiintyvien vakioiden mittayksiköt? Kiinteät tuotantokustannukset ovat 9000 (mk/kk). Muodosta funktio, joka ilmoittaa hyödykkeen tuotantokustannukset 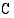 (mk/kk) tuotantonopeuden
(mk/kk) tuotantonopeuden 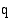 (kpl/kk) funktiona. Laske, kuinka paljon kustannukset kasvavat, kun tuotantonopeutta lisätään arvosta 100 (kpl/kk) arvoon 101 (kpl/kk). Vertaan tulosta rajakustannuksiin tuotantonopeudella 100 (kpl/kk).
(kpl/kk) funktiona. Laske, kuinka paljon kustannukset kasvavat, kun tuotantonopeutta lisätään arvosta 100 (kpl/kk) arvoon 101 (kpl/kk). Vertaan tulosta rajakustannuksiin tuotantonopeudella 100 (kpl/kk).
10. Eräällä alueella Lapissa mäkäräisten lukumäärä kasvaa suotuisissa olosuhteissa nopeudella
missä 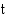 (vrk) on aika tarkastelun alkuhetkestä. Kuinka paljon alueella oli mäkäräisiä 14 (vrk):n kuluttua, kun niitä oli aluksi 10000 (kpl)?
(vrk) on aika tarkastelun alkuhetkestä. Kuinka paljon alueella oli mäkäräisiä 14 (vrk):n kuluttua, kun niitä oli aluksi 10000 (kpl)?