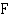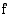6.2.1. Integraalifunktion määritelmä

Edellä etsittiin funktioita, joiden derivaatta kasvunopeutta esittävä funktio on. Tuloksena saatu funktio on kasvunopeusfunktion integraalifunktio. Funktio 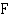on funktion 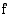integraalifunktio, jos

määrittelyjoukon jokaisella muuttujan arvolla 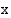. Merkitään

Integraalifunktion määrittämistä kutsutaan integroinniksi. Integraalimerkinnässä 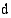-kirjaimen jäljessä oleva tunnus ilmoittaa muuttujan, jonka suhteen integroidaan.

Funktiolla on äärettömän monta integraalifunktiota. Jos funktio 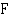on funktion 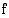integraalifunktio, niin kaikki funktiot, jotka ovat muotoa 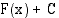, missä 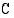on jokin vakio, ovat myös funktion 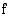integraalifunktioita, sillä 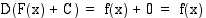. Voidaan osoitaa, että jos funktio 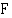on funktion 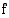jokin integraalifunktio, niin funktion 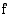kaikki integraalifunktiot ovat muotoa 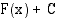, missä 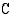on jokin vakio. Vakiota 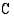kutsutaan integroimisvakioksi.

Esimerkki 6.3.

Määrää funktion 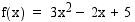kaikki integraalifunktiot.

Ratkaisu:

Vastaus:   Integraalifunktiot ovat muotoa .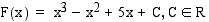

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]