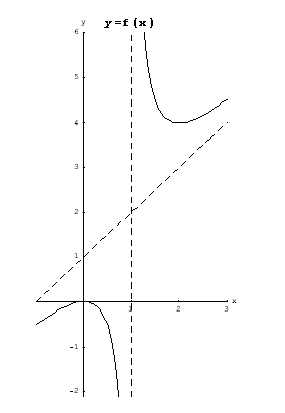
Rationaalifunktion kuvaaja
Raja-arvo äärettömyydessä
Rationaalifunktion kuvaajan piirtämistä varten on tärkeää tietää, mitä funktion arvoille tapahtuu 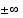 :ssä. Tämän ilmoittaa funktion
raja-arvo äärettömyydessä.
:ssä. Tämän ilmoittaa funktion
raja-arvo äärettömyydessä.
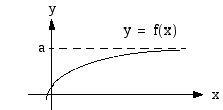 Funktiolla
Funktiolla 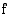 on raja-arvo
on raja-arvo 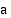 , kun muuttujan arvot kasvavat rajatta, jos aina jostakin muuttujan arvosta lähtien funktion
, kun muuttujan arvot kasvavat rajatta, jos aina jostakin muuttujan arvosta lähtien funktion 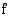 arvot saadaan miten tahansa lähelle lukua
arvot saadaan miten tahansa lähelle lukua 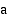 . Tätä raja-arvoa merkitään
. Tätä raja-arvoa merkitään
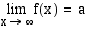
tai 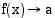 , kun
, kun 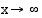 . Esimerkiksi
. Esimerkiksi
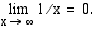
Vastaavasti sanotaan, että funktiolla 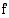 on raja-arvo
on raja-arvo 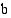 , kun muuttujan arvot vähenevät rajatta, jos aina jotakin muuttujan arvoa pienemmillä luvuilla funktion
, kun muuttujan arvot vähenevät rajatta, jos aina jotakin muuttujan arvoa pienemmillä luvuilla funktion 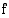 arvot saadaan miten tahansa lähelle lukua
arvot saadaan miten tahansa lähelle lukua 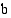 . Tätä raja-arvoa merkitään
. Tätä raja-arvoa merkitään
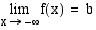
tai 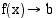 , kun
, kun 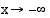 .
.
Esimerkki 5.26.
Määrää raja-arvo
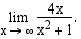
Ratkaisu:
Raja-arvon määrittämistä varten otetaan sekä osoittajassa että nimittäjässä korkeinta astetta oleva muuttujan potenssi yhteiseksi tekijäksi ja supistetaan. Raja-arvo saadaan määrättyä, kun tämän jälkeen käytetään tietoa
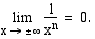
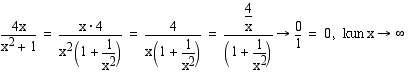
Vastaus: 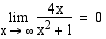
Esimerkki 5.27.
Määrää raja-arvo
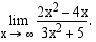
Ratkaisu:
Otetaan tässäkin sekä osoittajassa että nimittäjässä korkeinta astetta oleva muuttujan potenssi yhteiseksi tekijäksi ja supistetaan. Päätellään raja-arvo jäljelle jäävästä lausekkeesta.
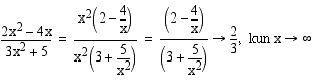
Vastaus: 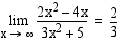
Asymptootit
Rationaalifunktion kuvaajalla on aina vähintään yksi
asymptootti, joka on sellainen suora tai käyrä, jota funktion kuvaaja jatkuvasti lähestyy, mutta ei koskaan saavuta. Jokaisella rationaalifunktiolla on asymptootti, joka kuvaa funktion kulkua 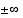 :ssä. Lisäksi rationaalifunktion kuvaajalla on pystysuora asymptootti jokaisessa nimittäjän nollakohdassa. Lähestyttäessä tätä kohtaa oikealta tai vasemmalta, funktion arvot aina kasvavat tai vähenevät rajatta. (Tässä oletetaan, että rationaalifunktion lauseke on supistetussa muodossa.)
:ssä. Lisäksi rationaalifunktion kuvaajalla on pystysuora asymptootti jokaisessa nimittäjän nollakohdassa. Lähestyttäessä tätä kohtaa oikealta tai vasemmalta, funktion arvot aina kasvavat tai vähenevät rajatta. (Tässä oletetaan, että rationaalifunktion lauseke on supistetussa muodossa.)
Rationaalifunktion kulkua 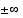 :ssä kuvaava asymptootti riippuu osoittajan ja nimittäjän asteluvuista.
:ssä kuvaava asymptootti riippuu osoittajan ja nimittäjän asteluvuista.
• Jos osoittaja on alempaa astetta kuin nimittäjä, asymptoottina on 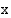 -akseli eli suora
-akseli eli suora 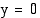 . Tällöin funktion raja-arvo
. Tällöin funktion raja-arvo 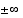 :ssä on aina nolla (vrt. esim. 5.25).
:ssä on aina nolla (vrt. esim. 5.25).
• Jos rationaalifunktion 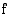 osoittaja ja nimittäjä ovat samaa astetta, funktion kuvaajalla on asymptoottina
osoittaja ja nimittäjä ovat samaa astetta, funktion kuvaajalla on asymptoottina 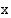 -akselin suuntainen suora
-akselin suuntainen suora 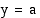 , missä
, missä
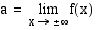 .
.
• Jos rationaalifunktion osoittajan asteluku on suurempi kuin nimittäjän asteluku, sen kuvaajalla on asymptoottina suora tai käyrä, jonka yhtälö saadaan suorittamalla jakolasku ja "unohtamalla" jakojäännöstermi, joka lähestyy aina nollaa, kun muuttujan arvot kasvavat tai vähenevät rajatta. Esimerkiksi funktio
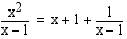 .
.
(Saatu suorittamalla jakolasku jakokulmassa.) Kun 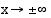 ,
, 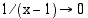 , jolloin funktion kuvaaja lähestyy suoraa
, jolloin funktion kuvaaja lähestyy suoraa 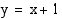 , mikä on funktion kuvaajan asymptootti.
, mikä on funktion kuvaajan asymptootti.
Kuvaajan piirtäminen
Rationaalifunktion kuvaaja voidaan hahmottaa selvittämällä funktion monotonisuus sekä kuvaajan ääriarvopisteet ja asymptootit.
Esimerkki 5.28.
Piirrä funktion
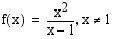
kuvaaja.
Ratkaisu:
Edellä tehdyn tarkastelun perusteella funktion kuvajalla on asymptoottina suora 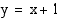 . Koska kohta
. Koska kohta 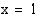 on funktion nimittäjän nollakohta, sen kuvaajalla on asymptoottina pystysuora suora
on funktion nimittäjän nollakohta, sen kuvaajalla on asymptoottina pystysuora suora 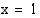 .
.
Selvitetään vielä funktion monotonisuus sekä lokaalit ääriarvot. Funktio 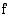 on derivoituva määrittelyjoukossaan, joten sen ainoat mahdolliset ääriarvokohdat ovat derivaatan nollakohdat. Funktion derivatta on
on derivoituva määrittelyjoukossaan, joten sen ainoat mahdolliset ääriarvokohdat ovat derivaatan nollakohdat. Funktion derivatta on
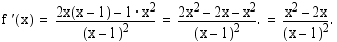
Ratkaistaan derivaatan nollakohdat.
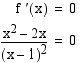
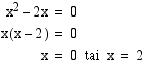
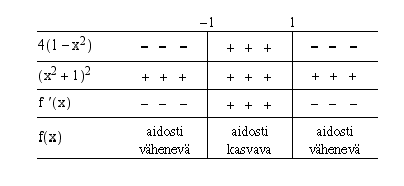
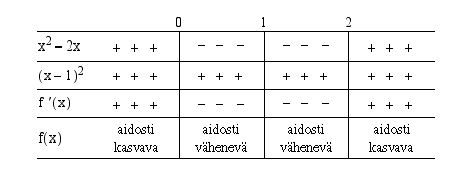
Selvitetään funktion monotonisuus sekä ääriarvojen laatu derivaatan merkkikaavion avulla.
Kaavion perusteella funktio 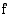 muuttuu aidosti kasvavasta aidosti väheneväksi kohdassa
muuttuu aidosti kasvavasta aidosti väheneväksi kohdassa 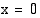 , joten funktiolla on lokaali maksimi
, joten funktiolla on lokaali maksimi 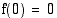 . Kohdassa
. Kohdassa 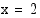 funktio
funktio 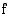 muuttuu aidosti vähenevästä aidosti kasvavaksi, joten funktiolla on tässä kohdassa lokaali minimi
muuttuu aidosti vähenevästä aidosti kasvavaksi, joten funktiolla on tässä kohdassa lokaali minimi
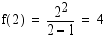 .
.
Koska funktion kuvaajalla on pystysuora asymptootti 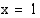 ja funktio on aidosti vähenevä, kun
ja funktio on aidosti vähenevä, kun 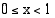 , funktion arvot vähenevät rajatta, kun
, funktion arvot vähenevät rajatta, kun 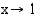 vasemmalta eli
vasemmalta eli
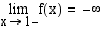 .
.
Kun 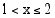 , funktio
, funktio 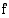 on myös aidosti vähenevä. Koska
on myös aidosti vähenevä. Koska 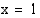 on kuvaajan asymptootti, funktion arvot kasvavat rajatta, kun lähestytään kohtaa
on kuvaajan asymptootti, funktion arvot kasvavat rajatta, kun lähestytään kohtaa 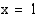 oikealta eli
oikealta eli
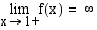 .
.
Funktion käyttäytymisen kohdan 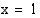 läheisyydessä voi päätellä myös tutkimalla funktion lauseketta. Kun
läheisyydessä voi päätellä myös tutkimalla funktion lauseketta. Kun 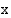 lähestyy lukua 1 vasemmalta, funktion osoittaja lähestyy lukua 1 ja nimittäjä lukua 0 ollen koko ajan negatiivinen, jolloin osamäärä vähenee rajatta. Kun
lähestyy lukua 1 vasemmalta, funktion osoittaja lähestyy lukua 1 ja nimittäjä lukua 0 ollen koko ajan negatiivinen, jolloin osamäärä vähenee rajatta. Kun 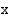 :n arvot lähestyvät lukua 1 oikealta, osoittaja lähestyy edelleen lukua 1 ja nimittäjä lukua 0, mutta nyt nimittäjä on positiivinen, jolloin osamäärä kasvaa rajatta.
:n arvot lähestyvät lukua 1 oikealta, osoittaja lähestyy edelleen lukua 1 ja nimittäjä lukua 0, mutta nyt nimittäjä on positiivinen, jolloin osamäärä kasvaa rajatta.
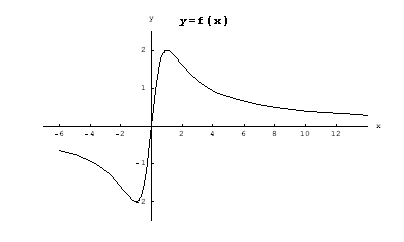
Funktion kuvaajan voi nyt piirtää asymptoottien, ääriarvojen sekä monotonisuuden avulla. Jos haluaa tarkemman kuvan, voi laskea kuvaajalta joitakin lisäpisteitä.
Vastaus:
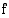 on kohdassa
on kohdassa 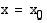 lokaali minimi (lokaali maksimi)
lokaali minimi (lokaali maksimi) 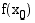 , jos kohdan
, jos kohdan 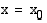 läheisyydessä jokaisessa pisteessä
läheisyydessä jokaisessa pisteessä 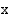 on voimassa
on voimassa 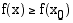 (
(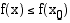 ). Kohtaa
). Kohtaa 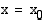 kutsutaan tällöin
ääriarvokohdaksi (minimi- tai maksimikohta) ja funktion arvoa
kutsutaan tällöin
ääriarvokohdaksi (minimi- tai maksimikohta) ja funktion arvoa 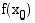 ääriarvoksi (minimi- tai maksimiarvo).
ääriarvoksi (minimi- tai maksimiarvo). 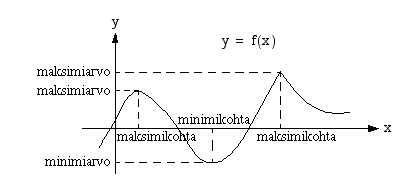
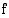 jatkuva. Tällöin kohta, jossa funktio muuttuu aidosti vähenevästä aidosti kasvavaksi, on funktion minimikohta. Jos funktio
jatkuva. Tällöin kohta, jossa funktio muuttuu aidosti vähenevästä aidosti kasvavaksi, on funktion minimikohta. Jos funktio 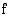 muuttuu kohdassa päinvastoin aidosti kasvavasta aidosti väheneväksi, kohta on funktion maksimikohta. Tällainen kohta voi olla derivaatan nollakohta, johon piirretty tangentti on vaakasuora, tai kohta, jossa funktio ei ole derivoituva (esim. kärkikohta). Jos siis funktio
muuttuu kohdassa päinvastoin aidosti kasvavasta aidosti väheneväksi, kohta on funktion maksimikohta. Tällainen kohta voi olla derivaatan nollakohta, johon piirretty tangentti on vaakasuora, tai kohta, jossa funktio ei ole derivoituva (esim. kärkikohta). Jos siis funktio 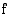 on jatkuva kohdassa
on jatkuva kohdassa 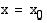 ja derivoituva jossakin tämän kohdan ympäristössä, niin kohta
ja derivoituva jossakin tämän kohdan ympäristössä, niin kohta 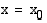 , jossa
, jossa 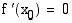 tai
tai 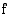 ei ole derivoituva, on
ei ole derivoituva, on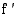 muuttuu tässä kohdassa negatiivisesta positiiviseksi.
muuttuu tässä kohdassa negatiivisesta positiiviseksi.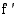 muuttuu tässä kohdassa positiivisesta negatiiviseksi.
muuttuu tässä kohdassa positiivisesta negatiiviseksi. 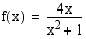
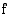 on määritelty koko reaalilukujen joukossa ja se on rationaalifunktiona tässä joukossa derivoituva. Funktion ainoat mahdolliset ääriarvokohdat ovat siten derivaatan nollakohdat. Funktion derivaatta on
on määritelty koko reaalilukujen joukossa ja se on rationaalifunktiona tässä joukossa derivoituva. Funktion ainoat mahdolliset ääriarvokohdat ovat siten derivaatan nollakohdat. Funktion derivaatta on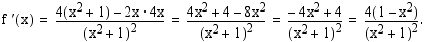
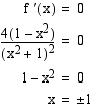
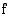 muuttuu kohdassa
muuttuu kohdassa 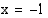 aidosti vähenevästä aidosti kasvavaksi, kohta
aidosti vähenevästä aidosti kasvavaksi, kohta 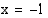 on minimikohta ja funktion minimiarvo tässä kohdassa on
on minimikohta ja funktion minimiarvo tässä kohdassa on 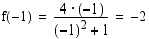 .
. 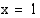 funktio
funktio 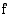 muuttuu aidosti kasvavasta aidosti väheneväksi, joten
muuttuu aidosti kasvavasta aidosti väheneväksi, joten 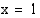 on funktion maksimikohta. Funktion maksimiarvo on tässä kohdassa
on funktion maksimikohta. Funktion maksimiarvo on tässä kohdassa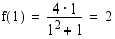 .
. 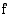 ääriarvot ovat: minimi
ääriarvot ovat: minimi 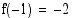 ja maksimi
ja maksimi 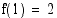 .
.
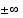 :ssä. Tämän ilmoittaa funktion
raja-arvo äärettömyydessä
:ssä. Tämän ilmoittaa funktion
raja-arvo äärettömyydessä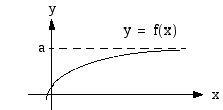 Funktiolla
Funktiolla 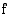 on raja-arvo
on raja-arvo 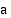 , kun muuttujan arvot kasvavat rajatta, jos aina jostakin muuttujan arvosta lähtien funktion
, kun muuttujan arvot kasvavat rajatta, jos aina jostakin muuttujan arvosta lähtien funktion 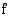 arvot saadaan miten tahansa lähelle lukua
arvot saadaan miten tahansa lähelle lukua 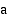 . Tätä raja-arvoa merkitään
. Tätä raja-arvoa merkitään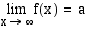
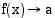 , kun
, kun 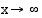 . Esimerkiksi
. Esimerkiksi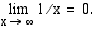
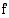 on raja-arvo
on raja-arvo 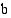 , kun muuttujan arvot vähenevät rajatta, jos aina jotakin muuttujan arvoa pienemmillä luvuilla funktion
, kun muuttujan arvot vähenevät rajatta, jos aina jotakin muuttujan arvoa pienemmillä luvuilla funktion 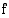 arvot saadaan miten tahansa lähelle lukua
arvot saadaan miten tahansa lähelle lukua 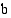 . Tätä raja-arvoa merkitään
. Tätä raja-arvoa merkitään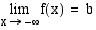
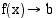 , kun
, kun 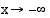 .
.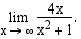
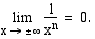
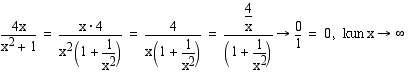
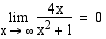
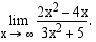
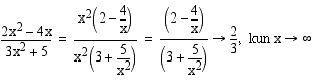
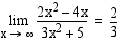
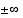 :ssä. Lisäksi rationaalifunktion kuvaajalla on pystysuora asymptootti jokaisessa nimittäjän nollakohdassa. Lähestyttäessä tätä kohtaa oikealta tai vasemmalta, funktion arvot aina kasvavat tai vähenevät rajatta. (Tässä oletetaan, että rationaalifunktion lauseke on supistetussa muodossa.)
:ssä. Lisäksi rationaalifunktion kuvaajalla on pystysuora asymptootti jokaisessa nimittäjän nollakohdassa. Lähestyttäessä tätä kohtaa oikealta tai vasemmalta, funktion arvot aina kasvavat tai vähenevät rajatta. (Tässä oletetaan, että rationaalifunktion lauseke on supistetussa muodossa.) 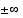 :ssä kuvaava asymptootti riippuu osoittajan ja nimittäjän asteluvuista.
:ssä kuvaava asymptootti riippuu osoittajan ja nimittäjän asteluvuista.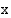 -akseli eli suora
-akseli eli suora 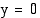 . Tällöin funktion raja-arvo
. Tällöin funktion raja-arvo 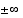 :ssä on aina nolla (vrt. esim. 5.25).
:ssä on aina nolla (vrt. esim. 5.25).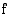 osoittaja ja nimittäjä ovat samaa astetta, funktion kuvaajalla on asymptoottina
osoittaja ja nimittäjä ovat samaa astetta, funktion kuvaajalla on asymptoottina 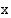 -akselin suuntainen suora
-akselin suuntainen suora 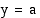 , missä
, missä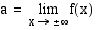 .
. 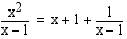 .
. 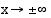 ,
, 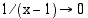 , jolloin funktion kuvaaja lähestyy suoraa
, jolloin funktion kuvaaja lähestyy suoraa 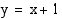 , mikä on funktion kuvaajan asymptootti.
, mikä on funktion kuvaajan asymptootti. 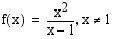
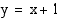 . Koska kohta
. Koska kohta 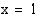 on funktion nimittäjän nollakohta, sen kuvaajalla on asymptoottina pystysuora suora
on funktion nimittäjän nollakohta, sen kuvaajalla on asymptoottina pystysuora suora 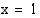 .
. 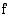 on derivoituva määrittelyjoukossaan, joten sen ainoat mahdolliset ääriarvokohdat ovat derivaatan nollakohdat. Funktion derivatta on
on derivoituva määrittelyjoukossaan, joten sen ainoat mahdolliset ääriarvokohdat ovat derivaatan nollakohdat. Funktion derivatta on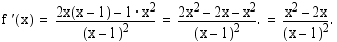
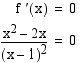
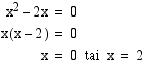
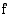 muuttuu aidosti kasvavasta aidosti väheneväksi kohdassa
muuttuu aidosti kasvavasta aidosti väheneväksi kohdassa 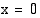 , joten funktiolla on lokaali maksimi
, joten funktiolla on lokaali maksimi 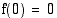 . Kohdassa
. Kohdassa 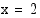 funktio
funktio 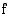 muuttuu aidosti vähenevästä aidosti kasvavaksi, joten funktiolla on tässä kohdassa lokaali minimi
muuttuu aidosti vähenevästä aidosti kasvavaksi, joten funktiolla on tässä kohdassa lokaali minimi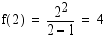 .
. 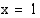 ja funktio on aidosti vähenevä, kun
ja funktio on aidosti vähenevä, kun 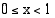 , funktion arvot vähenevät rajatta, kun
, funktion arvot vähenevät rajatta, kun 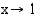 vasemmalta eli
vasemmalta eli 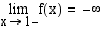 .
. 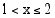 , funktio
, funktio 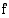 on myös aidosti vähenevä. Koska
on myös aidosti vähenevä. Koska 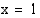 on kuvaajan asymptootti, funktion arvot kasvavat rajatta, kun lähestytään kohtaa
on kuvaajan asymptootti, funktion arvot kasvavat rajatta, kun lähestytään kohtaa 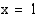 oikealta eli
oikealta eli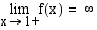 .
. 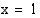 läheisyydessä voi päätellä myös tutkimalla funktion lauseketta. Kun
läheisyydessä voi päätellä myös tutkimalla funktion lauseketta. Kun 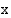 lähestyy lukua 1 vasemmalta, funktion osoittaja lähestyy lukua 1 ja nimittäjä lukua 0 ollen koko ajan negatiivinen, jolloin osamäärä vähenee rajatta. Kun
lähestyy lukua 1 vasemmalta, funktion osoittaja lähestyy lukua 1 ja nimittäjä lukua 0 ollen koko ajan negatiivinen, jolloin osamäärä vähenee rajatta. Kun 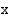 :n arvot lähestyvät lukua 1 oikealta, osoittaja lähestyy edelleen lukua 1 ja nimittäjä lukua 0, mutta nyt nimittäjä on positiivinen, jolloin osamäärä kasvaa rajatta.
:n arvot lähestyvät lukua 1 oikealta, osoittaja lähestyy edelleen lukua 1 ja nimittäjä lukua 0, mutta nyt nimittäjä on positiivinen, jolloin osamäärä kasvaa rajatta.