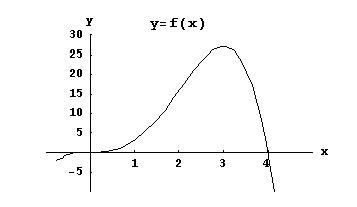
5.5.1. Funktion kasvaminen ja väheneminen
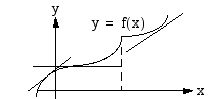 Jos tietyllä välillä jatkuvan funktion kuvaajalle piirretyt tangentit ovat nousevia suoria, funktio on tällä välillä aidosti kasvava. Kuvasta nähdään, että välillä saa olla yksittäisiä pisteitä (ei kokonaista väliä), joissa tangentti on vaakasuora tai joissa funktio ei ole derivoituva (kärkikohta tai tangentti pystysuora).
Jos tietyllä välillä jatkuvan funktion kuvaajalle piirretyt tangentit ovat nousevia suoria, funktio on tällä välillä aidosti kasvava. Kuvasta nähdään, että välillä saa olla yksittäisiä pisteitä (ei kokonaista väliä), joissa tangentti on vaakasuora tai joissa funktio ei ole derivoituva (kärkikohta tai tangentti pystysuora).
Jos funktio 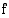 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 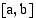 ja
ja 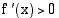 koko välillä lukuunottamatta yksittäisiä pisteitä, joissa
koko välillä lukuunottamatta yksittäisiä pisteitä, joissa 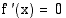 tai
tai 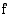 ei ole derivoituva, niin funktio
ei ole derivoituva, niin funktio 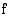 on aidosti kasvava välillä
on aidosti kasvava välillä 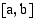 .
.
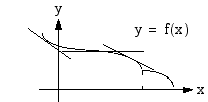 Vastaavasti, jos tietyllä välillä jatkuvan funktion kuvajalle piirretyt tangentit ovat laskevia suoria, funktio on tällä välillä aidosti vähenevä. Välillä saa olla erillisiä pisteitä (ei kuitenkaan kokonaista väliä), joihin piirretty tangentti on vaakasuora tai joissa funktio ei ole derivoituva. Kuva osoittaa, että funktio on edelleen aidosti vähenevä.
Vastaavasti, jos tietyllä välillä jatkuvan funktion kuvajalle piirretyt tangentit ovat laskevia suoria, funktio on tällä välillä aidosti vähenevä. Välillä saa olla erillisiä pisteitä (ei kuitenkaan kokonaista väliä), joihin piirretty tangentti on vaakasuora tai joissa funktio ei ole derivoituva. Kuva osoittaa, että funktio on edelleen aidosti vähenevä.
Jos funktio 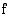 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 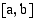 ja
ja 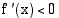 koko välillä lukuunottamatta yksittäisiä pisteitä, joissa
koko välillä lukuunottamatta yksittäisiä pisteitä, joissa 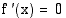 tai
tai 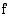 ei ole derivoituva, niin funktio
ei ole derivoituva, niin funktio 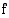 on aidosti vähenevä välillä
on aidosti vähenevä välillä 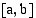 .
.
Esimerkki 5.24.
Millä väleillä polynomifunktio 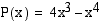 on (a) aidosti kasvava (b) aidosti vähenevä? Piirrä myös tämän funktion kuvaaja.
on (a) aidosti kasvava (b) aidosti vähenevä? Piirrä myös tämän funktion kuvaaja.
Ratkaisu:
Tutkitaan funktion kasvamista ja vähenemistä derivaatan merkkikaavion avulla. Funktion derivaatta on 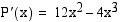 . Derivaatan merkkikaavion laatimista varten lasketaan derivaatan nollakohdat.
. Derivaatan merkkikaavion laatimista varten lasketaan derivaatan nollakohdat.
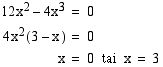
Päätellään funktion kasvaminen ja väheneminen seuraavasta derivaatan merkkikaaviosta:
Vastaus: Polynomifunktio 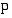 on aidosti kasvava, kun
on aidosti kasvava, kun 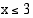 , ja aidosti vähenevä, kun
, ja aidosti vähenevä, kun 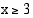 . Funktion kuvaajalle piirretyt tangentit ovat vaakasuoria derivaatan nollakohdissa
. Funktion kuvaajalle piirretyt tangentit ovat vaakasuoria derivaatan nollakohdissa 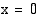 ja
ja 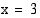 . Funktion arvot näissä kohdissa ovat
. Funktion arvot näissä kohdissa ovat 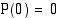 ja
ja 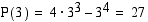 . Funktion kuvaajan voi hahmottaa näiden tietojen perusteella.
. Funktion kuvaajan voi hahmottaa näiden tietojen perusteella.
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
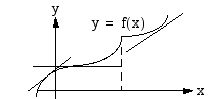 Jos tietyllä välillä jatkuvan funktion kuvaajalle piirretyt tangentit ovat nousevia suoria, funktio on tällä välillä aidosti kasvava. Kuvasta nähdään, että välillä saa olla yksittäisiä pisteitä (ei kokonaista väliä), joissa tangentti on vaakasuora tai joissa funktio ei ole derivoituva (kärkikohta tai tangentti pystysuora).
Jos tietyllä välillä jatkuvan funktion kuvaajalle piirretyt tangentit ovat nousevia suoria, funktio on tällä välillä aidosti kasvava. Kuvasta nähdään, että välillä saa olla yksittäisiä pisteitä (ei kokonaista väliä), joissa tangentti on vaakasuora tai joissa funktio ei ole derivoituva (kärkikohta tai tangentti pystysuora). 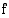 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä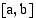 ja
ja 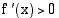 koko välillä lukuunottamatta yksittäisiä pisteitä, joissa
koko välillä lukuunottamatta yksittäisiä pisteitä, joissa 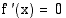 tai
tai 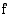 ei ole derivoituva, niin funktio
ei ole derivoituva, niin funktio 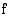 on aidosti kasvava
on aidosti kasvava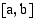 .
.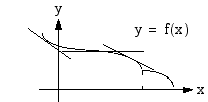 Vastaavasti, jos tietyllä välillä jatkuvan funktion kuvajalle piirretyt tangentit ovat laskevia suoria, funktio on tällä välillä aidosti vähenevä. Välillä saa olla erillisiä pisteitä (ei kuitenkaan kokonaista väliä), joihin piirretty tangentti on vaakasuora tai joissa funktio ei ole derivoituva. Kuva osoittaa, että funktio on edelleen aidosti vähenevä.
Vastaavasti, jos tietyllä välillä jatkuvan funktion kuvajalle piirretyt tangentit ovat laskevia suoria, funktio on tällä välillä aidosti vähenevä. Välillä saa olla erillisiä pisteitä (ei kuitenkaan kokonaista väliä), joihin piirretty tangentti on vaakasuora tai joissa funktio ei ole derivoituva. Kuva osoittaa, että funktio on edelleen aidosti vähenevä.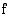 on jatkuva suljetulla välillä
on jatkuva suljetulla välillä 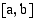 ja
ja 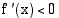 koko välillä lukuunottamatta yksittäisiä pisteitä, joissa
koko välillä lukuunottamatta yksittäisiä pisteitä, joissa 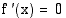 tai
tai 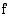 ei ole derivoituva, niin funktio
ei ole derivoituva, niin funktio 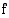 on aidosti vähenevä
on aidosti vähenevä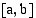 .
.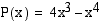 on (a) aidosti kasvava (b) aidosti vähenevä? Piirrä myös tämän funktion kuvaaja.
on (a) aidosti kasvava (b) aidosti vähenevä? Piirrä myös tämän funktion kuvaaja.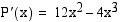 . Derivaatan merkkikaavion laatimista varten lasketaan derivaatan nollakohdat.
. Derivaatan merkkikaavion laatimista varten lasketaan derivaatan nollakohdat.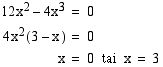
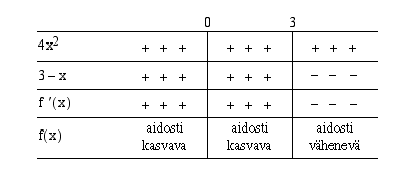
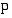 on aidosti kasvava, kun
on aidosti kasvava, kun 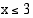 , ja aidosti vähenevä, kun
, ja aidosti vähenevä, kun 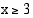 . Funktion kuvaajalle piirretyt tangentit ovat vaakasuoria derivaatan nollakohdissa
. Funktion kuvaajalle piirretyt tangentit ovat vaakasuoria derivaatan nollakohdissa 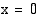 ja
ja 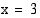 . Funktion arvot näissä kohdissa ovat
. Funktion arvot näissä kohdissa ovat 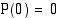 ja
ja 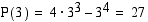 . Funktion kuvaajan voi hahmottaa näiden tietojen perusteella.
. Funktion kuvaajan voi hahmottaa näiden tietojen perusteella.