[Etusivu] [Sisällysluettelo] [Hakemisto]
[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]

---

Vakiofunktion derivaatta

Vakiofunktion derivaatta on nolla:

 

Olkoon , missä on vakio. Tällöin

 

Vakiolla kerrotun funktion derivaatta

Jos funktio 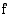kerrotaan vakiolla 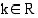ja tämä funktio derivoidaan, tulos on funktion 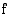derivaatta kerrottuna vakiolla :

 

Olkoon funktio . Tällöin

 

Funktioiden summan derivaatta

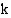Kahden funktion summan derivaatta on funktioiden derivaattojen summa:

 

Tämä derivoimissääntö voidaan todistaa samoin kuin aiemmatkin. Todistuksen yksityiskohdat jätetään lukijalle harjoitustehtäväksi.

Potenssifunktion derivaatta

Potenssifunktion 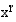, missä eksponentti 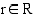, derivaattafunktio on

 

Tästä lähtien derivoimissääntöjen todistukset sivuutetaan. Ne löytyvät differentiaalilaskennan oppikirjoista.

Esimerkki 5.13.

Derivoi polynomifunktio .

Ratkaisu:

Edellä esitettyjen sääntöjen nojalla polynomi voidaan derivoida termeittäin.

 

Vastaus:   

Esimerkki 5.14.

Derivoi funktio .

Ratkaisu:

Tulkitaan funktio 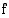potenssifunktioksi: 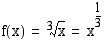. Tällöin

 

Vastaus:   

Huom!

Kuutiojuurifunktio ei ole derivoituva kohdassa 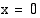. Funktion kuvajalle tähän kohtaan piirretty tangentti on pystysuora, jolloin sillä ei ole kulmakerrointa. Itse asiassa mikään juurifunktio 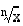ei ole derivoituva nollassa tästä syystä.

Funktioiden 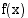tulon derivaatta

Funktioiden ja 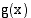tulofunktion 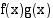derivaattafunktio on

 

Esimerkki 5.15.

Derivoi funktio .

Ratkaisu:

Käytetään tulon derivoimissääntöä:

 

Vastaus:   

Huom!

Tässä tapauksessa voi tietysti ensin suorittaa kertolaskun ja derivoida sitten saadun polynomifunktion. Lukija voi tarkistaa tuloksen derivoimalla funktion myös tällä tavalla.

Funktioiden 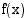osamäärän derivaatta

Funktioiden ja 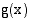osamäärän 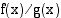derivaattafunktio on

 

Esimerkki 5.16.

Derivoi funktio

 

Ratkaisu:

Osamäärän derivoimissäännön nojalla

 

Vastaus:   

Yhdistetyn funktion derivaatta

Funktioist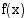a ja 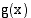muodostetun yhdistetyn funktion 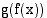derivaatta on

 

Yhdistetyn funktion derivaatta muodostetaan sijoittamalla ulkofunktion 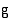derivaattafunktioon 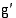muuttujan paikalle sisäfunktion 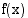lauseke. Saatu lauseke kerrotaan vielä sisäfunktion derivaattafunktiolla.

Esimerkki 5.17.

Derivoi funktio .

Ratkaisu:

Funktio 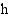voidaan ajatella yhdistetyksi funktioksi seuraavasti: 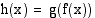, missä sisäfunktio 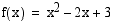ja ulkofunktio 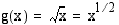. Sovelletaan yhdistetyn funktion derivoimissääntöä.

 

Vastaus:   

Esimerkki 5.18.

Derivoi funktio

 

Ratkaisu:

Funktio 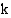voidaan tulkita yhdistetyksi funktioksi esim. siten, että 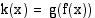, missä sisäfunktio 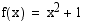ja ulkofunktio 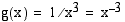. Kun tähän tulkintaan sovelletaan yhdistetyn funktion derivoimissääntöä, saadaan

 

Kun funktio 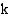tulkitaan yhdistetyksi funktioksi siten, että 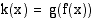, missä sisäfunktio 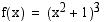ja ulkofunktio 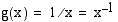, funktion derivaataksi saadaan

 

Yhdistetyn funktion derivaataksi saadaan siis aina sama funktio, vaikka se tulkittaisiin yhdistetyksi funktioksi eri tavoin.

Vastaus:   

 

Edellisessä luvussa esitellyt alkeisfunktiot ovat määrittelyjoukossaan derivoituvia. Seuraavaksi esitellään niiden derivoimissäännöt, joita ei myöskään todisteta tällä kurssilla.

Eksponenttifunktion derivaatta

Eksponenttifunktion 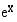derivaatta on funktio itse: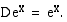

Yhdistetyssä funktiossa 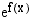on sisäfunktiona 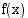ja ulkofunktiona 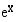, jolloin sen derivaatta on

 

Esimerkki 5.19.

Derivoi funktio .

Ratkaisu:

 

Vastaus:   

Muiden eksponenttifunktioiden derivointi onnistuu samojen sääntöjen avulla, sillä jokainen eksponenttifunktio 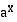voidaan kirjoittaa muodossa 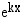, missä 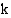on jokin reaalilukuvakio. Koska kantaluku 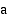voidaan ilmaista Neperin luvun 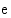potenssina: 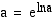, on funktio

 

Eksponenttifunktion 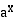derivaatta on siten

 

Näin saatiin yleinen eksponenttifunktion derivointisääntö:

 

Yhdistetyn funktion 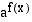derivaatta on

 

Esimerkki 5.20.

Argentiinan väkiluku 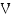(milj.) 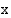vuoden kuluttua vuodesta 1994 laskettuna on

 

Kuinka suuri oli väestön kasvunopeus tämän arvion mukaan Argentiinassa vuonna 1997?

Ratkaisu:

Väestön kasvunopeuden ilmoittaa funktion 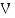derivaattafunktio.

 

Vuonna 1997 väestön kasvunopeus oli Argentiinassa

 

Vastaus:   V. 1997 Argentiinan väestön kasvunopeus oli n. 496000 (asukasta/vuosi).

Logaritmifunktion derivaatta

Luonnollisen logaritmifunktion 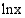derivaatta on

 

Yhdistetyssä funktiossa 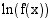on sisäfunktiona 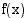ja ulkofunktiona 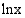. Kun sovelletaan tähän yhdistetyn funktion derivoimissääntöä, saadaan

 

Esimerkki 5.21.

Derivoi funktio .

Vastaus:   

 

Muut logaritmifunktiot voidaan myös derivoida näiden sääntöjen avulla, kun ne muutetaan ensin kannanvaihtokaavalla luonnollisiksi logaritmeiksi. Koska

 

on yleisen logaritmifunktion derivaatta

 

Trigonometristen funktioiden derivaatat

Sinifunktion derivaatta on kosinifunktio:

 

Yhdistetyssä funktiossa 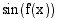on sisäfunktiona 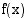ja ulkofunktiona 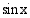. Tämän funktion derivaatta on siten

 

Kosinifunktion derivaatta on

 

jolloin yhdistetyn funktion 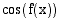derivaatta on

 

Esimerkki 5.22.

Vuoroveden takia veden korkeus 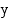(m) vaihtelee satamassa noudattaen funktiota

 

missä 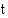on keskiyöstä kulunut aika tunteina. Millä nopeudella veden korkeus muuttuu satamassa klo 8.00?

Ratkaisu:

Veden korkeuden muutosnopeus on korkeusfunktion derivaatta:

 

Klo 8.00 korkeus muuttuu nopeudella

 

Vastaus:   Klo 8.00 veden korkeus laskee nopeudella n. 60 (cm/h).