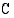(mk/kk) tuotantonopeuden 
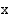(kpl/kk) funktiona ovat
Oton Puu valmistaa sorvattuja kukkapylväitä. Yhden pylvään valmistuskustannukset materiaalikuluineen ovat 75 (mk/kpl). Lisäksi yrityksen kiinteät tuotantokustannukset ovat 1200 (mk/kk). Tällöin yrityksen tuotantokustannukset 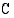(mk/kk) tuotantonopeuden 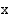(kpl/kk) funktiona ovat
Muodosta funktio, joka ilmoittaa tuotantokustannusten ja tuotantonopeuden välisen riippuvuussuhteen kääntäen, eli mikä on tiettyjä tuotantokustannuksia vastaava tuotantonopeus.
Olkoot tuotantokustannukset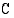 
(mk/kk) (
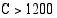). Määrätään niitä vastaava tuotantonopeus ratkaisemalla 
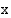seuraavasta yhtälöstä.
Vastaus: Tuotantokustannuksia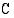 
(mk/kk) vastaava tuotantonopeus 
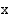(kpl/kk) on
Edellisessä esimerkissä määrättiin tuotantokustannusfunktion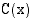 
käänteisfunktio 
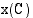, joka liitti tuotantokustannuksiin sitä vastaavan tuotantonopeuden, eli se liitti jokaiseen funktion 
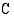arvoon sitä vastaavan muuttujan 
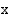arvon.
Olkoon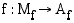 
jokin funktio. Sen
käänteisfunktio on funktio 
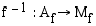, joka liittää jokaiseen arvojoukon 
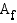alkioon 
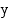sitä vastaavan määrittelyjoukon alkion 
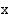, jolle 
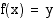. Funktiolla ja sen käänteisfunktiolla on yhteys
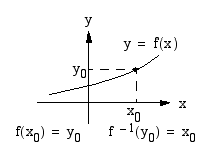
Kaikilla funktioilla ei ole käänteisfunktiota. Liitettäessä jokaiseen arvojoukon alkioon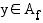 
sitä vastaava(t) määrittelyjoukon alkio(t) 
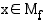, jo(i)lle 
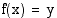, ei aina muodostu funktiota. Määritelmän mukaan funktion on liitettävä jokaiseen alkioon täsmälleen yksi alkio. Jos funktio saa arvon 
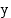useassa eri pisteessä, liittyy tähän arvojoukon alkioon useita eri määrittelyjoukon alkioita, eikä riippuvuussuhde määrittele funktiota. Käänteisfunktio on ainoastaan sellaisella funktiolla 
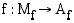, joka saa jokaisen arvonsa täsmälleen yhdessä määrittelyjoukon pisteessä. Vaakasuora suora 
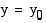, missä 
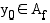, leikkaa tällaisen funktion kuvaajan täsmälleen kerran. Esimerkiksi kaikilla aidosti monotonisilla funktioilla on tämä ominaisuus.
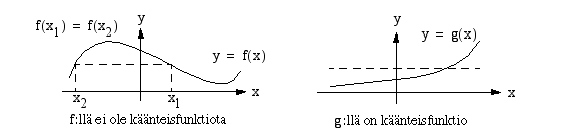
Jos piirretään funktion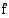 
ja sen käänteisfunktion 
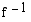kuvaajat samaan koordinaatistoon, havaitaan niiden olevan symmetriset suoran 
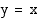suhteen. Jos 
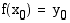, on funktion 
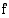kuvaajalla piste 
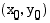. Tällöin 
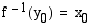, joten käänteisfunktion 
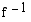kuvaajalla on piste
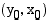. Nämä pisteet ovat symmetriset suoran 
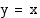suhteen. Symmetriaominaisuuden perusteella käänteisfunktion kuvaaja voidaan hahmottaa alkuperäisen funktion kuvaajan avulla.
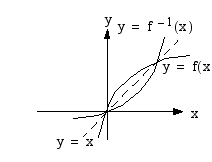
Muodosta funktion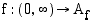 
, 
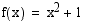, käänteisfunktio, jos se on olemassa.
Funktion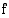 
kuvaaja on ylöspäin aukeavan paraabelin oikeanpuoleinen haara, joten se on määrittelyjoukossaan aidosti kasvava ja sillä on käänteisfunktio. Funktion 
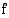arvojoukko on 
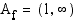, joten sen käänteisfunktion 
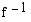määrittelyjoukko on 
.
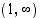Määrätään käänteisfunktion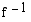 
lauseke ratkaisemalla 
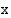yhtälöstä 
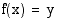, kun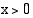 
.
Käänteisfunktion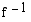 
lauseke on 
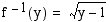. Kun vaihdetaan käänteisfunktion muuttujaksi 
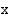, saadaan 
.
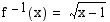Funktion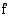 
käänteisfunktion 
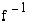määrittelyjoukko on 
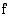:n arvojoukko: 
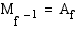, ja toisaalta käänteisfunktion arvojoukko on alkuperäisen funktion määrittelyjoukko: 
.
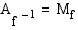5. Olkoot funktiot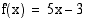 
ja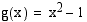 
. Muodosta yhdistetyt funktiot
6. Millä vakion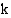 
arvoilla 
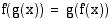, kun 
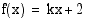ja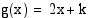 
?
7. Mikä on ulkofunktio ja mikä sisäfunktio, kun yhdistetty funktio on
8. Määrää funktion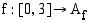 
, 
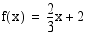, käänteisfunktio. Piirrä 
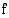:n ja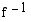 
:n kuvaajat samaan koordinaatistoon.
9. Funktiolla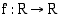 
, 
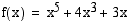, on käänteisfunktio 
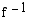. Laske 
.
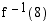10. Funktiolla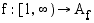 
, 
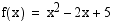, on käänteisfunktio 
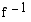. Muodosta 
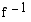ja ratkaise yhtälö 
.
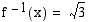11. Opiskelijan vuosipalkasta toimitetaan ennakonpidätys seuraavasti: 38000 (mk):aan asti vero on 26 %, ja ylimenevästä osasta 42 %. Muodosta funktio, joka ilmoittaa opiskelijan vuosittaisen nettopalkan vuositulojen funktiona. Muodosta lisäksi tämän funktion käänteisfunktio. Mitä se ilmoittaa?
12. Eskon työmatka on 45 (km). Alkumatkasta on 10 (km) tietä, jolla nopeusrajoitus on 50 (km/h). Tämän jälkeen alkaa valtatie, jolla nopeus saa olla 80 (km/h). Loppumatkasta on 5 (km) moottoritietä, jolla nopeusrajoitus on 100 (km/h). Muodosta funktio, joka ilmoittaa Eskon kulkeman matkan käytetyn ajan funktiona, kun hän käyttää työmatkallaan suurinta sallittua ajonopeutta. Muodosta myös tämän funktion käänteisfunktio.
, 
