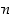Variaatio ja kombinaatio

Tarkastellaan nyt, kuinka monella tavalla jostakin äärellisestä joukosta voidaan muodostaa erisuuruisia osajoukkoja. Erilaiset tulokset saadaan siitä riippuen, onko alkioiden valintajärjestyksellä merkitystä. Jos on, puhutaan variaatioista, jos ei, puhutaan kombinaatioista.

Lause 6.1.4.

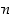−alkioisen joukon alkioista voidaan muodostaa

erilais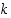ta :n alkion järjestettyä jonoa eli variaatiota ().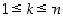

Todistus. Tuloperiaatteen mukaan ensimmäinen alkio voidaan valita 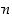eri tavalla, toinen jäljelle jääneistä 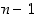tavalla jne. Lopuksi viimeinen eli 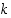:s alkio voidaan valita 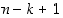tavalla.

Lause 6.1.5.

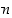−alkioisen joukon alkioista voidaan muodostaa

erilais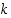ta :n alkion osajoukkoa eli kombinaatiota ().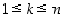

Todistus. Olkoon 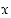kyseinen kombinaatioiden lukumäärä. Jokaisesta 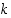:n alkion osajoukosta voidaan muodostaa 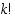erilaista järjestettyä jonoa. Siten

,

mistä ratkaistuna on

Esimerkki 6.1.6.

Laatikossa olkoon 12 lamppua, joista tiedetään, että 3 on viallista. Kuinka monella tavalla laatikosta voidaan valita kaksi lamppua? Entä kuinka monella tavalla kaksi ehjää lamppua?

Nostomahdollisuuksia on kaikkiaan

Ehjien lamppujen nostomahdollisuuksia on taasen

Opiskelutehtävä 54. (Shakkiotteluiden määrä)

Shakkikerhon peliturnaukseen tulee 10 pelaajaa. Kuinka monta ottelua tarvitaan, jos jokainen pelaa kerran jokaisen muun kanssa? Entä jos jokainen pelaa kerran sekä valkeilla että mustilla pelinappuloilla jokaista muuta vastaan?

Vinkki tehtävään 54

Edellä esiintyneitä lukuja 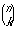sanotaan binomikertoimiksi. Niille on voimassa kaavat

    

     Pascalin sääntö

Lisäksi pätee ns. Pascalin binomikaava

kaikilla reaaliluvuilla 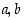ja positiivisilla kokonaisluvuilla 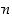. Tämän todistus voidaan tehdä induktiolla. Erikoistapauksena tästä kaavasta saadaan, että

eli

Tämä ilmaisee, lause 6.1.5 huomioiden, että 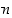−alkioisella joukolla on yhteensä 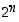erilaista osajoukkoa (0−alkioista, 1−alkioista, … , (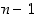)−alkioista ja 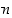−alkioista). Tämän takia osajoukkojen muodostamaa joukkoa sanotaankin potenssijoukoksi.

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]