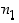 eri tavalla ja toinen sen jälkeen aina ensimmäisen vaiheen tuloksesta riippumatta
eri tavalla ja toinen sen jälkeen aina ensimmäisen vaiheen tuloksesta riippumatta 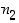 eri tavalla, voi ilmiö yhteensä tapahtua
eri tavalla, voi ilmiö yhteensä tapahtua 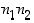 eri tavalla.
eri tavalla.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Ennen todennäköisyyden käsitteeseen perehtymistä tarkastelemme paria kombinatorista tapaa muodosta erilaisia äärellisiä osajoukkoja. Vastaavilla tavoilla voidaan kuvata monien satunnaisilmiöiden etenemistä.
Jos jokin ilmiö voi tapahtua kahdessa peräkkäisessä vaiheessa niin, että ensimmäinen voi tapahtua 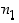 eri tavalla ja toinen sen jälkeen aina ensimmäisen vaiheen tuloksesta riippumatta
eri tavalla ja toinen sen jälkeen aina ensimmäisen vaiheen tuloksesta riippumatta 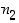 eri tavalla, voi ilmiö yhteensä tapahtua
eri tavalla, voi ilmiö yhteensä tapahtua 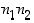 eri tavalla.
eri tavalla.
Yleistyksenä saadaan: Jos ilmiö voi tapahtua 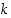 peräkkäisellä vaiheella niin, että
peräkkäisellä vaiheella niin, että 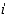 :s vaihe voi tapahtua
:s vaihe voi tapahtua 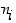 eri tavalla, voi koko ilmiö tapahtua yhteensä
eri tavalla, voi koko ilmiö tapahtua yhteensä 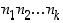 eri tavalla.
eri tavalla.
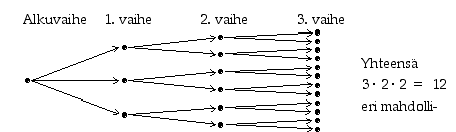
Tavallisessa vakioveikkauksessa veikataan kolmeatoista kohdetta ja kussakin kohteessa on kolme vaihtoehtoa (1, X tai 2). Erilaisia veikkausrivejä on siten tuloperiaatteen mukaan 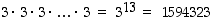 kappaletta.
kappaletta.
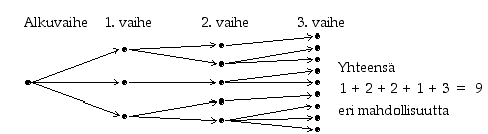
Jos jokin ilmiö voi tapahtua kahdella toisensa poissulkevalla (tai vaihtoehtoisella) tavalla niin, että ensimmäisellä tavalla on 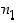 eri tulosmahdollisuutta ja toisella
eri tulosmahdollisuutta ja toisella 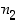 eri tulosmahdollisuutta, voi ilmiö tapahtua yhteensä
eri tulosmahdollisuutta, voi ilmiö tapahtua yhteensä 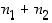 eri tavalla.
eri tavalla.
Yleistyksenä tästä saadaan: Jos jokin ilmiö voi sattua 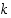 toisensa poissulkevalla tavalla niin, että
toisensa poissulkevalla tavalla niin, että 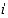 :nnella tavalla on
:nnella tavalla on 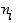 eri tulosmahdollisuutta, voi koko ilmiö tapahtua yhteensä
eri tulosmahdollisuutta, voi koko ilmiö tapahtua yhteensä 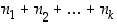 eri tavalla.
eri tavalla.
Säännöllisen dodekaedrin seitsemän tahkoa olkoot maalattu punaiseksi ja loput viisi keltaiseksi. Noppaa heitetään kaksi kertaa. Tulosvaihtoehtoja on nyt neljä: kahdesti punainen tahko, kahdesti keltainen tahko, ensin punainen tahko ja sitten keltainen tahko sekä ensin keltainen tahko ja sitten punainen tahko. Selvitetään näiden mahdollisuuksien kokonaismäärät.
Tuloperiaatteen mukaan eri tahkoparit voivat tulla tulokseksi 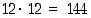 eri tavalla. Näistä molemmilla kerroilla voi punainen tahko tulla
eri tavalla. Näistä molemmilla kerroilla voi punainen tahko tulla 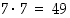 eri tavalla ja molemmilla kerroilla keltainen tahko
eri tavalla ja molemmilla kerroilla keltainen tahko 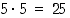 eri tavalla. Ensin punainen tahko ja sitten keltainen tahko voi tulla
eri tavalla. Ensin punainen tahko ja sitten keltainen tahko voi tulla 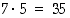 eri tavalla ja ensin keltainen tahko ja sitten punainen tahko voi taas tulla
eri tavalla ja ensin keltainen tahko ja sitten punainen tahko voi taas tulla 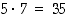 eri tavalla.
eri tavalla.
Voidaan kysyä myös, kuinka monella tavalla tulokseksi voi tulla toisella kerralla punainen ja toisella keltainen tahko (järjestyksestä riippumatta). Summa- ja tuloperiaatteiden mukaan näin voi tapahtua 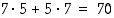 tavalla.
tavalla.
Eräässä viestintäjärjestelmässä on käytössä kolme erilaista lippua, joista viestin lähettämiseksi pannaan vähintään yksi tankoon. Kuinka monta erilaista viestiä voidaan lähettää, jos lippujen järjestyksellä on merkitystä?
On kolme vaihtoehtoista menetelmää sijoittaa liput: tankoon pannaan yksi, kaksi tai kolme lippua. Yhden lipun sijoittamiseen on vain kolme mahdollisuutta. Kaksi lippua voidaan panna tuloperiaatteen mukaan 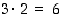 eri tavalla. Ja kolme lippua
eri tavalla. Ja kolme lippua 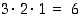 tavalla. Yhteensä on summaperiaatteen mukaan
tavalla. Yhteensä on summaperiaatteen mukaan 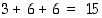 erilaista lippujen sijoitustapaa eli viestimahdollisuutta.
erilaista lippujen sijoitustapaa eli viestimahdollisuutta.