[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tässä pykälässä tarkastelemme kolmiulotteisia säännöllisiä kappaleita sekä niiden kierto- ja symmetriaryhmiä.
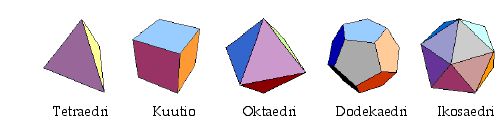
On varsin helppo keksiä kaksi tai kolmekin klassista säännöllistä monitahokasta eli avaruuden kappaletta, jotka ovat konvekseja (eli kärkien yhdysjanat eivät jää tahokkaan ulkopuolelle), ja joiden reuna muodostuu (aina samantyyppisistä) säännöllisistä monikulmioista. Yleisesti tuttuja ovat ainakin tetraedri ja kuutio sekä myös oktaedri (eli 4−, 6− ja 8−tahokkaat), joissa rakennussivuina käytetään kolmioita ja neliöitä. Pohdintojen tai kokeilujen jälkeen voi keksiä lisäksi dodekaedrin ja ikosaedrin (eli 12− ja 20−tahokkaat). Edellinen rakentuu viisikulmioista ja jälkimmäinen taas kolmioista, mutta siis useammasta kuin tetraedri tai oktaedri. Alla ovat mainittujen monitahokkaitten kuvat.

Onko muita tällä tavalla konstruoitavia kappaleita? Jos ei, niin miksi ei? Tarkastellaan tilannetta palauttamalla ongelma tasokuvioihin. Säännöllisistä monitahokkaista voidaan aina tehdä ns. Schlegelin tasokuvio ''katsomalla yhden tahkon läpi'' tai ''venyttämällä yhden tahkon särmät'' (ja niiden myötä osin muitakin särmiä) sillä tavalla, että ne ympäröivät kaikki muut. Alla ovat yllämainituista monitahokkaista tällä tavalla saatavat Schlegelin kuviot.
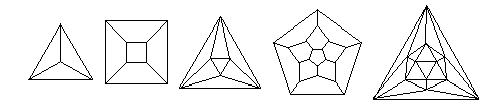
Tällainen kuvio muodostuu monitahokkaan kärjistä (eli solmupisteistä), särmistä (yhdysviivoista) ja tahkoista (alueista). Se on myös yhtenäinen, ts. jokaisesta kärjestä pääsee särmiä pitkin mihin tahansa muuhun kärkeen. Tarkastellaan tarkemmin tällaisia yhtenäisiä tasograafeja, jotka muodostuvat pisteistä ja niitä yhdistävistä, toisiaan leikkaamattomista viivoista sekä niiden rajaamista tason alueista. Yhdistävien viivojen ei välttämättä tarvitse olla suoraviivaisia, vaan ne voivat olla esimerkiksi kaarevia.
Yhtenäisessä pisteistä ja niitä yhdistävistä, toisiaan leikkaamattomista viivoista muodostuvassa tasokuviossa pätee kaava
missä 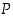 on pisteiden,
on pisteiden, 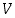 viivojen ja
viivojen ja 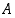 alueiden lukumäärä.
alueiden lukumäärä.
Todistus. Jokainen tällainen yhtenäinen kuvio voidaan ajatella muodostuneen yhdestä pisteestä lisäämällä siihen viivoja ja pisteitä. Yhden pisteen muodostamalle kuviolle pätee, että 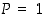 ,
,
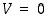 ja
ja 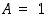 (koko taso), joten sille yhtälö
(koko taso), joten sille yhtälö 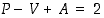 pätee.
pätee.
Jos sitten johonkin yhtenäiseen kuvioon halutaan lisätä uusi piste tai viiva, se voidaan tehdä oleellisesti kahdella eri tavalla: joko lisäämällä uusi piste ja yhdistämällä se johonkin olemassaolleeseen pisteeseen tai sitten lisäämällä vain kahta olemassaolevaa pistettä yhdistävä viiva.
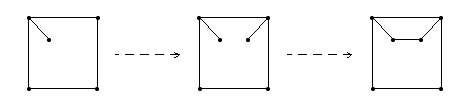
Edellisessä tapauksessa luvut 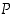 ja
ja 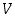 kasvavat yhdellä, mutta
kasvavat yhdellä, mutta 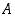 pysyy ennallaan. Jälkimmäisessä tapauksessa luku
pysyy ennallaan. Jälkimmäisessä tapauksessa luku 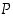 pysyy ennallaan, mutta luvut
pysyy ennallaan, mutta luvut 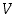 ja
ja 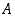 kasvavat yhdellä. Kummassakaan tapauksessa lausekkeen
kasvavat yhdellä. Kummassakaan tapauksessa lausekkeen 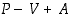 arvo ei muutu.
arvo ei muutu.
Päättelemmekin siten induktiivisesti, että jokaiselle tarkasteltavalle kuviolle summa 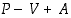 on aivan sama kuin mitä se on yksinkertaisimmalle mahdolliselle eli yhden pisteen kuviolle. Toisin sanoen kaava
on aivan sama kuin mitä se on yksinkertaisimmalle mahdolliselle eli yhden pisteen kuviolle. Toisin sanoen kaava 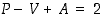 pätee kaikille väitteen mukaisille tasokuvioille.
pätee kaikille väitteen mukaisille tasokuvioille.
Jokaiselle monitahokkaalle pätee kaava
missä 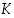 on kärkien,
on kärkien, 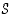 särmien ja
särmien ja 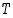 tahkojen lukumäärä.
tahkojen lukumäärä.
Todistus. Monitahokkaan Schlegelin kuvio on yhtenäinen tasograafi, joten väite seuraa edellisestä apulauseesta.
Tarkastellaan sitten mielivaltaista säännöllistä monitahokasta, joka muodostuu säännöllisistä 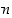 −kulmioista siten, että samaan kärkeen liittyy aina
−kulmioista siten, että samaan kärkeen liittyy aina 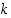 monikulmiota tahkoina. Olkoot edelleen
monikulmiota tahkoina. Olkoot edelleen 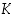 monitahokkaan kärkien lukumäärä,
monitahokkaan kärkien lukumäärä, 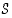 särmien lukumäärä ja
särmien lukumäärä ja 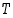 tahkojen lukumäärä.
tahkojen lukumäärä.
Koska jokaiseen kärkeen liittyy myös 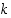 särmää
särmää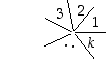 ,
saadaan yhtälö
,
saadaan yhtälö
(särmät tulevat laskettua kahteen kertaan).
Vastaavasti jokaiseen tahkoon liittyy 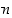 särmää
särmää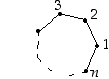 ,
joten pätee myös yhtälö
,
joten pätee myös yhtälö
Sijoitetaan nämä ehdot Eulerin kaavaan 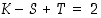 . Siten
. Siten
mistä saadaan edelleen seuraava päättelyketju:
Sijoittamalla tämä saadaan edelleen ratkaisut:
Koska luvut 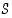 ,
,
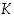 ja
ja 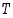 ovat kaikki positiivisia, saadaan edelleen seuraava päättelyketju:
ovat kaikki positiivisia, saadaan edelleen seuraava päättelyketju:
Koska on oltava 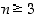 ja
ja 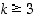 ,
on vain seuraavat vaihtoehdot:
,
on vain seuraavat vaihtoehdot:
• 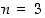 ja
ja 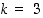 ,
jolloin saadaan tetraedri;
,
jolloin saadaan tetraedri;
• 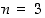 ja
ja 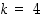 ,
jolloin saadaan oktaedri;
,
jolloin saadaan oktaedri;
• 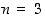 ja
ja 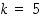 ,
jolloin saadaan ikosaedri;
,
jolloin saadaan ikosaedri;
• 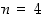 ja
ja 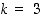 ,
jolloin saadaan kuutio;
,
jolloin saadaan kuutio;
• 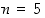 ja
ja 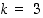 ,
jolloin saadaan dodekaedri.
,
jolloin saadaan dodekaedri.
Tuloksena on siis, että on olemassa vain nämä viisi säännöllistä monitahokasta, ns. Platonin kappaleet.
Opiskelutehtävä 48. (Tetraedrin sisäinen duaalikappale)
Yhdistä tetraedrin vierekkäisten tahkojen keskipisteet janoilla. Mikä monitahokas saadaan, kun nämä saadut janat ajatellaan sen särmiksi?
Jos sallitaan enemmän vaihtelua monitahokkaan tahkojen valinnoissa, saadaan kyllä enemmän monitahokkaita. Esimerkiksi jos sallitaan käytettävän useammanlaisia monikulmioita tahkoina, mutta edellytetään kuitenkin, että jokaisessa kärjessä tahkojen asettelu on täysin samanlainen, saadaan Platonin kappaleitten lisäksi ns. Arkhimedeen monitahokkaat, joita on kaikkiaan 13 erilaista. Jalkapallon malli perustuu mm. erääseen tällaiseen kappaleeseen, joka muodostuu 5− ja 6−kulmioista. Seuraavassa kuvassa ovat kaikki 13 Arkhimedeen monitahokasta kuvattuna.
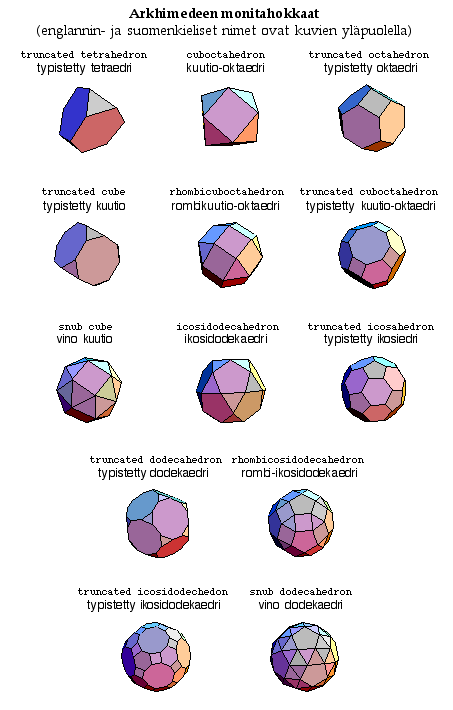
Arkhimedeen monitahokkaiden lisäksi on vielä olemassa ääretön määrä erikokoisia prismoja, joissa samanlaiset monikulmiot yhdistetään joko neliöillä (prisma) tai tasasivuisilla kolmioilla (vino prisma). Seuraavassa kuvassa ovat viisikulmioista muodostetut prismat.

Opiskelutehtävä 49. (Eulerin kaava Arkhimedeen monitahokkaalle)
Valitse yksi Arkhimedeen monitahokas ja selvitä päteekö sille Eulerin kaava.
Palataan säännöllisiin monitahokkaisiin eli Platonin kappaleisiin ja määrätään niiden kiertoryhmät. Tehdään se tarkemmin tetraedrille ja kuutiolle ja annetaan muille pelkkänä tuloksena.
Esimerkki 5.3.3. (Tetraedrin kiertoryhmä)
Numeroidaan säännöllisen tetraedrin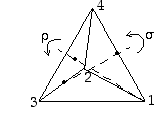 kärjet 1−4 ja määrätään sen kierrot permutaatioiden avulla samaan tapaan kuin tasossa tehtiin kolmiolle. Valitaan lähtökohdaksi kierrot
kärjet 1−4 ja määrätään sen kierrot permutaatioiden avulla samaan tapaan kuin tasossa tehtiin kolmiolle. Valitaan lähtökohdaksi kierrot
jolloin 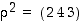 ja
ja 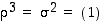 . Laskemalla havaitaan edelleen, että
. Laskemalla havaitaan edelleen, että
Permutaatioiden 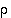 ja
ja 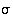 avulla on siis saatu aikaan alternoivan ryhmän
avulla on siis saatu aikaan alternoivan ryhmän 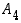 kaikki 12 alkiota. Toisaalta mitään tetraedrin kiertoa ei voi esittää yhdellä vaihdolla eikä siten millään parittomalla permutaatiolla (vaihdot esittävät nimittäin peilauksia), joten muita kuin ryhmän
kaikki 12 alkiota. Toisaalta mitään tetraedrin kiertoa ei voi esittää yhdellä vaihdolla eikä siten millään parittomalla permutaatiolla (vaihdot esittävät nimittäin peilauksia), joten muita kuin ryhmän 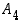 alkioita ei kiertoina tule kysymykseen. Tetraedrin kiertoryhmä on siis
alkioita ei kiertoina tule kysymykseen. Tetraedrin kiertoryhmä on siis 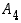 .
.
Esimerkki 5.3.4. (Kuution kiertoryhmä)
Kuution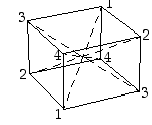 kierrot voidaan tietenkin esittää kahdeksan kärkipisteen tai kuuden tahkon permutaatioiden avulla. Ne voidaan kuitenkin esittää jo neljän objektin permutaatioina, kun tarkastellaan kuution neljän halkaisijan kuvautumisia. Numeroidaan kärkipisteet 1−4 siten, että vastakkaisilla kärjillä on sama numero, ts. numeroidaan halkaisijat.
kierrot voidaan tietenkin esittää kahdeksan kärkipisteen tai kuuden tahkon permutaatioiden avulla. Ne voidaan kuitenkin esittää jo neljän objektin permutaatioina, kun tarkastellaan kuution neljän halkaisijan kuvautumisia. Numeroidaan kärkipisteet 1−4 siten, että vastakkaisilla kärjillä on sama numero, ts. numeroidaan halkaisijat.
Jokainen kuution kierto permutoi halkaisijat toisikseen, joten ne voidaan esittää ryhmän 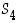 alkioilla. Valitaan peruskierroiksi
alkioilla. Valitaan peruskierroiksi
Koska nyt 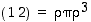 ,
,
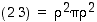 ja
ja 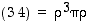 ,
edellisen luvun lauseen 4.2.6 mukaan kaikki permutaatiot voidaan esittää permutaatioiden
,
edellisen luvun lauseen 4.2.6 mukaan kaikki permutaatiot voidaan esittää permutaatioiden 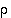 ja
ja 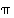 avulla. Jokainen ryhmän
avulla. Jokainen ryhmän 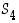 alkio esittää näin ollen jotain kiertoa tai niiden yhdistelyä. Kuution kiertoryhmä on siis
alkio esittää näin ollen jotain kiertoa tai niiden yhdistelyä. Kuution kiertoryhmä on siis 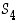 .
.
Kaikkien säännöllisten monitahokkaitten kiertoryhmät ilmenevät seuraavasta taulukosta:
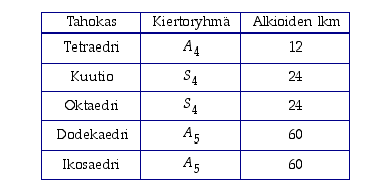
Yleisemmin voidaan osoittaa oikeaksi seuraava tulos.
Avaruuskappaleen äärellinen kiertoryhmä on oleellisesti jokin ryhmistä 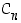 ,
,
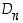 ,
,
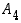 ,
,
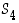 tai
tai 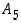 .
.
Kun kiertojen lisäksi otetaan huomioon mahdolliset peilaukset, saatu symmetriaryhmä tulee olemaan joko sama kuin kiertoryhmä tai sitten lukumäärältään kaksinkertainen. Seuraavassa taulukossa ovat lueteltuina säännöllisten monitahokkaitten symmetriaryhmät.
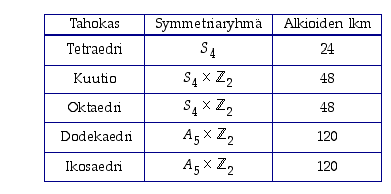
Siinä esimerkiksi 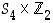 on tuloryhmä, joka saadaan ryhmästä
on tuloryhmä, joka saadaan ryhmästä 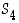 samaan tapaan kuin ryhmä
samaan tapaan kuin ryhmä 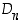 saadaan ryhmästä
saadaan ryhmästä 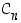 . Tarkempi selvitys samoin kuin taulukon tulosten todistus sivuutetaan.
. Tarkempi selvitys samoin kuin taulukon tulosten todistus sivuutetaan.
Opiskelutehtävä 50. (Eriväriset tetraedrit)
a) Käytettävissäsi on kahdenvärisiä tasasivuisia kolmioita. Kuinka monta erilaista tetraedria voit niistä muodostaa?
b) Entä kuinka monta erilaista tetraedria voit saada, jos voit käyttää (yksivärisen) tetraedrin kärkien värittämiseen kahta väriä (niin että kaikki kärjet väritetään)?
1. Todista kulmatarkastelujen avulla suoraan säännöllisille monitahokkaille ehto 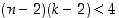 ,
missä
,
missä 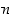 on yhden tahkon kulmien lukumäärä ja
on yhden tahkon kulmien lukumäärä ja 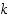 on tahokkaan yhteen kärkeen liittyvien tahkojen lukumäärä. (Vihje: Laske ensin
on tahokkaan yhteen kärkeen liittyvien tahkojen lukumäärä. (Vihje: Laske ensin 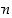 -kulmion sisäkulman suuruus ja päättele siitä ehto kulmien summalle tahokkaan kärjissä.)
-kulmion sisäkulman suuruus ja päättele siitä ehto kulmien summalle tahokkaan kärjissä.)
2. Tee taulukko, josta näkyy jokaiselle säännölliselle monitahokkaalle kärkien, särmien ja tahkojen lukumäärä. Tarkista, että Eulerin kaava pätee näille.
3. Esitä graafisesti tetraedrin kierroille tulon 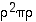 muodostuminen ja tarkista, että saamasi kierto vastaa laskemaasi permutaatiota.
muodostuminen ja tarkista, että saamasi kierto vastaa laskemaasi permutaatiota.
4. Määrää viereisen monitahokkaan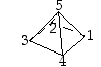 (suora 4−pyramidi, jonka kaikki sivut ovat yhtä pitkiä) kaikki kierrot ja peilaukset sekä sen kiertoryhmä.
(suora 4−pyramidi, jonka kaikki sivut ovat yhtä pitkiä) kaikki kierrot ja peilaukset sekä sen kiertoryhmä.
5. Yhdistä kuution vierekkäisten tahkojen keskipisteet janoilla. Mikä monitahokas saadaan, kun nämä saadut janat ajatellaan sen särmiksi? Mikä merkitys tällä tuloksella on?
6. Numeroi tetraedrin särmät 1−6. Esitä näiden permutaatioina kaikki tetraedrin 12 kiertoa.
7. Voit merkitä yksivärisen oktaedrin kärkiä kahdella värillä. Montako erilaista oktaedria saat aikaan?