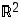kuvauksia, jotka säilyttävät kuviot samanlaisina. Kuvausta 
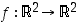sanotaan
isometriaksi, jos se säilyttää pisteiden etäisyydet, ts. jos kaikilla 
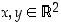on
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan seuraavassa lähemmin sellaisia tason 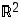kuvauksia, jotka säilyttävät kuviot samanlaisina. Kuvausta 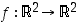sanotaan
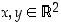isometriaksi, jos se säilyttää pisteiden etäisyydet, ts. jos kaikilla on
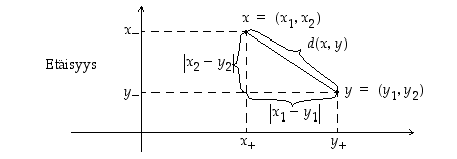
Tässä tason pisteiden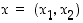 
ja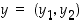 
etäisyys on ei-negatiivinen luku
(eli niiden erotusvektorin normi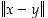 
,
ks. kuvio alla). Huomaa, että isometria on välttämättä bijektiivinen kuvaus.
Selvästi isometrioiden yhdistetyt kuvaukset samoin kuin käänteiskuvaukset ovat edelleen isometrioita.
Eräitä tason isometrioita on helppo tunnistaa. Seuraavissa esimerkeissä olevat kuvaukset ovat sellaisia. Näiden yhteydessä käytetään joitakin lineaarialgebrallisia merkintöjä ja tuloksia. Jos et ole vielä tutustunut vektorilaskentaan, käytä laskuissa annettuja lausekkeita. Myös huolellinen graafinen tarkastelu riittää yleensä vakuuttumaan tuloksista.
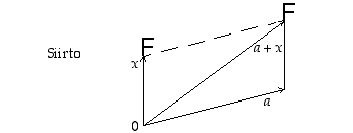
Siirto eli translaatio. Kun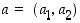 
on tason piste, on se tason yhdensuuntaissiirto, joka siirtää origon pisteeseen 
,
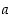eli kuvaus
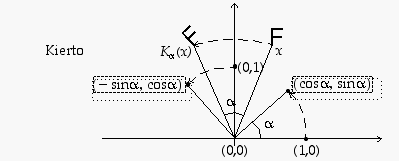
Kierto origon suhteen (eli rotaatio). Kun kierretään tasoa origon ympäri kulman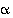 
verran, saadaan lineaarikuvaus
minkä laskemalla myös voi todeta olevan isometria.
Kierto tason pisteen suhteen. Kun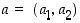 
on tason piste, saadaan sen ympäri tasoa kierrättävä kuvaus aikaan yhdistämällä siirto 
,
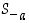kierto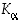 
ja siirto 
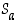takaisin:
Peilaus origosuoran suhteen (eli heijastus tai reflektio). Kun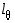 
on origon kautta kulkeva suora, jonka kulmakerroin on 
,
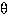on tason peilaus sen suoran suhteen lineaarikuvaus
Laskemalla on taas todettavissa, että tämä kuvaus tosiaan on isometria.
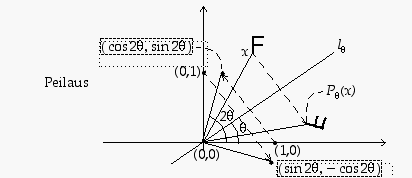
Peilaus suoran suhteen. Kun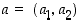 
on tason piste ja 
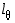on sen kautta kulkeva suora, jonka kulmakerroin on 
,
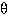saadaan peilaus tämän suoran kautta yhdistämällä siirto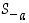 
,
peilaus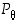 
ja siirto 
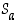takaisin:
Opiskelutehtävä 51. (Siirron, kierron ja peilauksen käänteiskuvaukset)
Selitä graafisesti ja lausekkein, millaisia ovat siirron, kierron ja peilauksen käänteiskuvaukset.
Kun sitten yhdistellään kiertoja origon ympäri ja peilauksia origon kautta kulkevien suorien suhteen, saadaan seuraavanlainen taulukko:
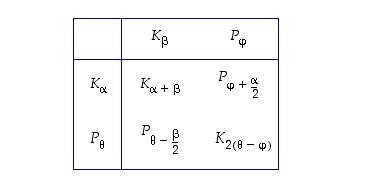
Kahden kierron tai kahden eri peilauksen yhdisteenä saadaan siis aina jokin kierto, ja jos taas yhdistetään kierto ja peilaus kummassa järjestyksessä vain, tulokseksi saadaan aina jokin peilaus (mutta ei yleensä samaa). Taulukossa esitetyt säännöt voidaan harjoitustehtävinä todentaa laskemalla kiertoihin ja peilauksiin liittyvien matriisien tuloja.
Opiskelutehtävä 52. (Kierron ja peilauksen tulot)
Keksi konkreettiset kulmat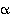 
ja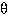 
siten, että 
.
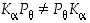Tehdään seuraavaksi eräitä lineaarialgebrallisia huomioita. Tasossa vektoreiden
sisätulosta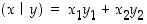 
saadaan vektorin
normi eli
pituus kaavalla
Pisteiden etäisyys voidaan nyt ilmoittaa käyttäen vektoreiden normimerkintää
Kun edellä normi saatiin sisätulosta, on myös toisinpäin: sisätulo saadaan normista ns. polarisaatiokaavan avulla:
Tämän seurauksena jokainen tason isometria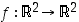 
,
joka kuvaa origon origoksi, säilyttää, paitsi etäisyydet eli normit, myös sisätulot, ts.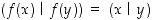 
kaikilla 
.
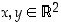Sellainen tason isometria, joka kuvaa origon origoksi, on joko kierto tai peilaus.
Todistus. Todistuksessa käytetään lineaarialgebran tietoja, jotka löytyvät esimerkiksi kirjasta Saarimäki: Vektoreita ja yhtälöitä. Olkoon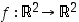 
isometria, jolle 
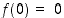. Tarkastellaan tason luonnollisen kannan 
,
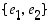missä 
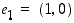ja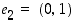 
,
kuvautumista. Koska se on ortonormaali kanta, edellä olevan huomion mukaan myös sen kuva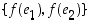 
on ortonormaali kanta. Jokaiselle 
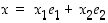on siten
joten piste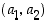 
sijaitsee yksikköympyrällä ja siten (napakoordinaatistossa) on olemassa kulma 
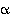siten, että 
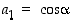ja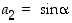 
. Koska edelleen yksikkövektori 
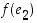on kohtisuorassa vektoria 
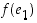vastaan, on
Ylemmillä etumerkeillä tulokseksi saadaan kierto kulman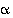 
verran ja alemmilla merkeillä saadaan tulokseksi peilaus sen suoran suhteen, jonka kulmakerroin on 
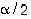. Lause on siten todistettu.
Tason isometria on jokin seuraavista:
(b) kierto jonkin tason pisteen ympäri,
(c) peilaus jonkin tason suoran suhteen, tai
(d) liukupeilaus, eli siirto yhdistettynä peilauksella siirron suuntaisen suoran suhteen.
Todistus. Olkoon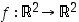 
isometria, jolloin siis
Jos isometria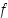 
pitää origon paikallaan, ts. 
,
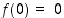edellisen lauseen mukaan se on kierto tai peilaus.
Jos taas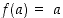 
jollekin pisteelle 
,
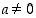kuvaa isometria 
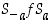origon origoksi ja on siis kierto tai peilaus. Itse 
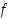on silloin joko kierto pisteen 
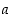ympäri tai peilaus pisteen 
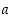kautta kulkevan suoran suhteen.
Jäljelle jää tapaus, jossa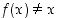 
kaikille tason pisteille 
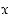. Kun nyt merkitään, että 
,
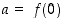kuvaa isometria 
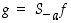origon origoksi ja siten se on kierto tai peilaus.
Jos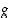 
on (epätäysi) kierto 
,
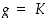kuvaus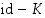 
on lineaarinen bijektio, ja siten löytyy vektori 
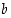siten, että 
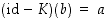eli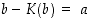 
. Tällöin 
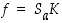ja siten
mikä on kuitenkin ristiriidassa sen oletuksen kanssa, että aina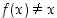 
. Siten 
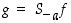ei voinut olla kierto.
Jos sitten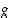 
on peilaus 
,
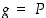valitaan
jolloin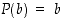 
,
ja lasketaan seuraavasti:
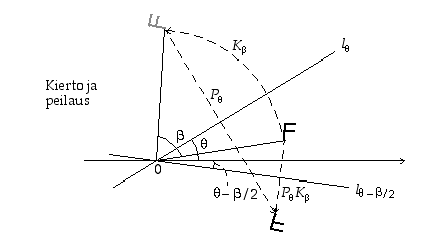
Kuvataan graafisesti liukupeilaus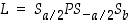 
:
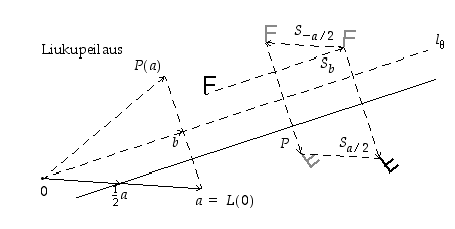
Opiskelutehtävä 53. (Peilauksen ja siirron yhdistetty kuvaus)
Yhdistä (graafisesti) peilaukseen siirto. Minkä tyyppinen isometria on tuloksena? Kokeile erisuuntaisia siirtoja. Miten tuloksena oleva isometria näyttäisi määräytyvän?
1. Osoita laskemalla, että tason kierto origon ympäri todella säilyttää etäisyydet.
2. Osoita laskemalla, että tason peilaus origon kautta kulkevan suoran suhteen todella säilyttää etäisyydet.
3. Kuvaa graafisesti yhtälöä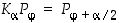 
. Piirrä pari oleellisesti erilaista tilannetta (voit valita myös varsin konkreetteja kulmia).
4. Kuvaa yhtälöä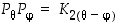 
. Piirrä pari oleellisesti erilaista tilannetta (voit valita myös varsin konkreetteja kulmia).
5. Selvitä funktion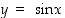 
kuvaajan kaikki mahdolliset symmetriakuvaukset (niitä on äärettömän monta). Kuvaa ja esitä ne mahdollisimman selkeästi.
6. Määrää alla olevien tasokuvioiden kaikki mahdolliset symmetriakuvaukset. Kuviot jatkuvat molempiin suuntiin samanlaisina sekä pikkuviivat leikkaavat akselia kokonaislukupisteissä. Pyri mahdollisimman selkeään esitykseen!
. 
. 
. 
: 
,
on 
. 
kaikilla 
. 
,
on liukupeilaus. 
