[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Suuriasteisille symmetrisille ryhmille niiden alkioiden tuloja on suoraan hankala määrätä, puhumattakaan kokonaisten kertolaskutaulukoiden tekemisestä. Permutaatioiden käsittelyn ja hahmottamisen helpottamiseksi on olemassa muutamia käyttökelpoisia esitystapoja.
Tarkastellaan ensin permutaatiossa 
graafisesti sen alkioiden kuvautumista. Voi huomata, että 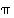 on eräänlainen 'kiertokuvaus': alkio 1 kuvautuu alkioksi 3, se kuvautuu alkioksi 4, se alkioksi 2, ja lopulta 2 takaisin alkioksi 1. Jos merkitsemme tällaista permutaatiota lyhyemmin
on eräänlainen 'kiertokuvaus': alkio 1 kuvautuu alkioksi 3, se kuvautuu alkioksi 4, se alkioksi 2, ja lopulta 2 takaisin alkioksi 1. Jos merkitsemme tällaista permutaatiota lyhyemmin 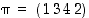 ,
voikin tästä itse asiassa jo lukea sen toiminnan.
,
voikin tästä itse asiassa jo lukea sen toiminnan.
tarkoittaa kiertoa (eli sykliä) ja tämä permutaatio määritellään asettamalla
Luku 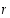 on kierron
on kierron 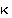 pituus ja
pituus ja 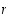 −pituista kiertoa sanotaan myös
−pituista kiertoa sanotaan myös 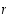 −
kierroksi. Kierron pituuden
−
kierroksi. Kierron pituuden 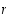 ei tarvitse olla sama kuin ryhmän aste
ei tarvitse olla sama kuin ryhmän aste 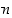 ,
vaan se voi olla pienempi. Ääritapauksena ryhmän
,
vaan se voi olla pienempi. Ääritapauksena ryhmän 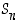 identtistä kuvausta
identtistä kuvausta 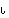 merkitsemme myös kiertomaisesti
merkitsemme myös kiertomaisesti 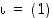 .
.
Seuraavat permutaatiot ovat kiertoja:
Ryhmän 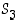 kaikki alkiot voidaan esittää kiertoina (käytämme edelleen esimerkkien 4.1.2 ja 4.1.8 merkintöjä):
kaikki alkiot voidaan esittää kiertoina (käytämme edelleen esimerkkien 4.1.2 ja 4.1.8 merkintöjä):
Kun aste 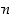 on suurempi kuin 3, eivät kaikki permutaatiot kuitenkaan enää ole kiertoja. Tarkastellaan esimerkkinä permutaatiota
on suurempi kuin 3, eivät kaikki permutaatiot kuitenkaan enää ole kiertoja. Tarkastellaan esimerkkinä permutaatiota
Tämä permutaatio kuvaa alkiot monessa ketjussa:
Graafisesti esitettynä näistä saadaan neljä osakuvausta:
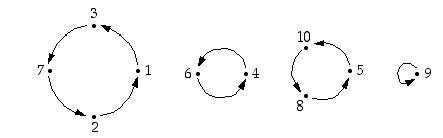
Nyt voimme esittää permutaation 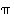 kolmen kierron tulona (neljäs osakuvaus ei muuta mitään):
kolmen kierron tulona (neljäs osakuvaus ei muuta mitään):
Sanomme, että kaksi kiertoa ovat
erilliset, jos niissä ei esiinny samoja alkioita. Yllä olevat kierrot (1 3 7 2), (4 6) ja (5 10 8) ovat siten erillisiä. Tällaisten erillisten kiertojen kertominen voidaan lisäksi suorittaa missä järjestyksessä tahansa. Siten permutaatio 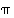 voidaan esittää myös mm. tuloina
voidaan esittää myös mm. tuloina
Opiskelutehtävä 38. (Permutaatio erillisten kiertojen tulona)
Edellä johdettu permutaatioesitys on esimerkki yleisemmästä tilanteesta.
Jokainen ryhmän 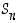 permutaatio (joka ei ole identtinen kuvaus) on joko itse kierto tai sitten se voidaan esittää erillisten kiertojen tulona.
permutaatio (joka ei ole identtinen kuvaus) on joko itse kierto tai sitten se voidaan esittää erillisten kiertojen tulona.
Todistus. Osoitetaan väite oikeaksi täydellisellä induktiolla. Ensimmäisessä tapauksessa 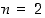 väite pitää paikkansa. Oletetaan sitten, että se pitää paikkansa kaikille
väite pitää paikkansa. Oletetaan sitten, että se pitää paikkansa kaikille 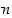 alkion permutaatioille. Induktioväitteen todistamiseksi olkoon
alkion permutaatioille. Induktioväitteen todistamiseksi olkoon 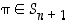 .
.
Jos 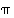 sattuu kuvaamaan alkion
sattuu kuvaamaan alkion 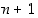 samaksi alkioksi
samaksi alkioksi 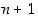 ,
se onkin olennaisesti
,
se onkin olennaisesti 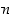 alkion permutaatio, ja siten väite pätee sille induktio-oletuksen mukaan.
alkion permutaatio, ja siten väite pätee sille induktio-oletuksen mukaan.
Olkoon sitten 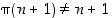 ja luku
ja luku 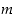 sellainen, että
sellainen, että 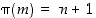 . Olkoon lisäksi
. Olkoon lisäksi 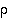 2−kierto
2−kierto 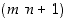 ja
ja 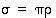 . Tällöin
. Tällöin 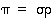 ,
sillä
,
sillä 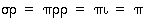 . Koska permutaatiolle
. Koska permutaatiolle 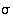 on nyt
on nyt
on se induktio-oletuksen mukaan joko kierto tai se voidaan esittää erillisten kiertojen tulona.
Jos myöskin 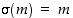 ,
niin joko
,
niin joko 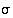 tai sen esityksen kaikki kierrot ovat erillisiä 2−kiertoon
tai sen esityksen kaikki kierrot ovat erillisiä 2−kiertoon 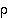 verrattuna. Mutta tällöinhän myös
verrattuna. Mutta tällöinhän myös 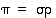 voidaan esittää erillisten kiertojen tulona.
voidaan esittää erillisten kiertojen tulona.
Jäljelle jää tapaus, jossa 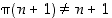 ja
ja 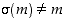 . Tällöin joko permutaatio
. Tällöin joko permutaatio 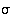 tai sen tuloesityksen yksi kierto kuvaa luvun
tai sen tuloesityksen yksi kierto kuvaa luvun 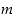 joksikin muuksi luvuksi. Niinpä
joksikin muuksi luvuksi. Niinpä 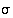 voidaan esittää muodossa
voidaan esittää muodossa
missä 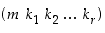 on kierto ja
on kierto ja 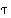 on joko identtinen kuvaus (jos
on joko identtinen kuvaus (jos 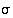 on jo itse kierto) tai sellaisten kiertojen tulo, jotka eivät muuta lukuja
on jo itse kierto) tai sellaisten kiertojen tulo, jotka eivät muuta lukuja 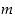 ,
,
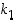 ,
,
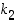 ,
…,
,
…, 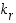 . Lisäksi tiedetään, että mikään edellä luetelluista luvuista ei ole luku
. Lisäksi tiedetään, että mikään edellä luetelluista luvuista ei ole luku 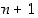 . Nyt saadaan permutaatiolle
. Nyt saadaan permutaatiolle 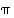 esitys
esitys
mikä osoittaa lopultakin, että 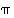 voidaan esittää erillisten kiertojen tulona.
voidaan esittää erillisten kiertojen tulona.
Ryhmän 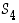 kaikki alkiot voidaan siis nyt esittää kiertojen avulla. Niistä saadaan seuraavanlainen taulukko.
kaikki alkiot voidaan siis nyt esittää kiertojen avulla. Niistä saadaan seuraavanlainen taulukko.
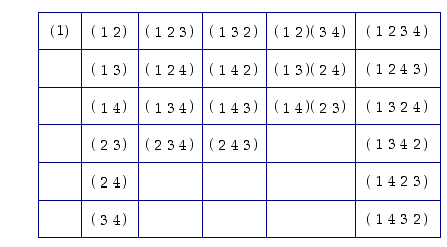
Huomaa, että koska permutoitavassa joukossa on vain neljä alkiota, kierrotkin voivat olla pituudeltaan korkeintaan neljä. Lisäksi vain 2−kierroista voidaan muodostaa erillisiä tuloja.
Opiskelutehtävä 39. (Permutaatiotulo erillisten kiertojen tulona)
Ilmoita permutaatiotulo 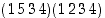 erillisten kiertojen tulona sekä myös kaksirivisessä esitysmuodossa.
erillisten kiertojen tulona sekä myös kaksirivisessä esitysmuodossa.
Opiskelutehtävä 40. (Käänteispermutaatio ja erillisten kiertojen tulo)
Määrää permutaatiolle 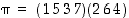 käänteispermutaatio ja esitä se erillisten kiertojen tulona. Vertaa tulosta alkuperäiseen esitykseen.
käänteispermutaatio ja esitä se erillisten kiertojen tulona. Vertaa tulosta alkuperäiseen esitykseen.
Lyhyintä mahdollista kiertoa eli 2−kiertoa 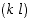 sanotaan myös
vaihdoksi eli
transpositioksi. On helppo nähdä, että jokainen kierto voidaan esittää vaihtojen tulona. Esimerkiksi
sanotaan myös
vaihdoksi eli
transpositioksi. On helppo nähdä, että jokainen kierto voidaan esittää vaihtojen tulona. Esimerkiksi
Yhdistämällä tämä huomio edelliseen lauseeseen saadaan seuraava tulos.
Jokainen permutaatio 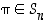 voidaan esittää vaihtojen tulona.
voidaan esittää vaihtojen tulona.
Vaihtojen tuloesitys ei kuitenkaan ole yksikäsitteinen, kuten seuraavassa pykälässä tarkemmin todetaan. Tarvitsemme myöhemmin vielä seuraavaa tulosta, joka ilmoittaa, että permutaatio voidaan esittää myös eräiden erityistyyppisten vaihtojen tulona.
Jokainen permutaatio 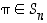 voidaan esittää vaihdoista
voidaan esittää vaihdoista
muodostettuna tulona. Se voidaan esittää aina myös vaihdoista
muodostettuna tulona. (Ääritapauksena tulossa voi olla vain yksi termi.)
Todistus. Ensimmäinen väite seuraa edellisestä lauseesta, kun huomataan, että mielivaltainen vaihto 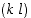 voidaan esittää tulona
voidaan esittää tulona
Toinen väite seuraa taas siitä, että edelleen
2. Ilmoita permutaatiotulo 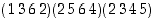 erillisten kiertojen tulona. Ilmoita se myös kaksirivisessä esitysmuodossa.
erillisten kiertojen tulona. Ilmoita se myös kaksirivisessä esitysmuodossa.
3. Tarkastellaan permutaatiota
(a) Ilmoita se erillisten kiertojen tulona.
(b) Ilmoita se vaihtojen tulona.
(c) Ilmoita se lauseen 4.2.6 mukaisten vaihtojen tulona.
4. Osoita, että ryhmässä 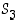 kierrolle
kierrolle 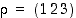 ja vaihdolle
ja vaihdolle 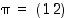 pätee, että
pätee, että 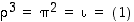 ja
ja 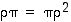 . Osoita edelleen, että koko ryhmän
. Osoita edelleen, että koko ryhmän 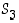 alkiot voidaan luetella muodossa
alkiot voidaan luetella muodossa 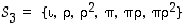 .
.
5. Anna ryhmissä 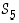 ,
,
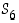 ja
ja 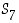 esimerkki kustakin erityyppisestä permutaation esityksestä erillisten kiertojen tulona. (Käytä lähtömallina ryhmää
esimerkki kustakin erityyppisestä permutaation esityksestä erillisten kiertojen tulona. (Käytä lähtömallina ryhmää 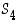 ,
missä kyseiset esimerkkityypit ovat
,
missä kyseiset esimerkkityypit ovat 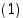 ,
,
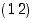 ,
,
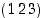 ,
,
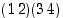 ja
ja 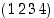 . Lukujen vaihtelua ei siis tarvitse huomioida.)
. Lukujen vaihtelua ei siis tarvitse huomioida.)
6. Olkoon 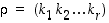 kierto ja
kierto ja 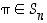 (
(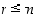 ). Osoita, että permutaatio
). Osoita, että permutaatio 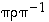 on myös kierto, ja että itse asiassa
on myös kierto, ja että itse asiassa 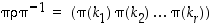 .
.
(a) Osoita, että permutaatio 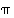 on oma käänteispermutaationsa täsmälleen silloin, kun
on oma käänteispermutaationsa täsmälleen silloin, kun 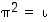 .
.
(b) Mitä voit sanoa sellaisen kierron pituudesta, joka on oma käänteispermutaationsa?
(c) Kuvaa edellisten kohtien perusteella, millaisia voivat olla ne permutaatiot 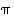 ,
joille
,
joille 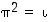 .
.
8. Jos permutaatio 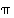 on esitetty erillisten kiertojen tulona, selvitä, miten tästä esityksestä saadaan käänteispermutaatiolle
on esitetty erillisten kiertojen tulona, selvitä, miten tästä esityksestä saadaan käänteispermutaatiolle 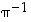 esitys erillisten kiertojen tulona.
esitys erillisten kiertojen tulona.