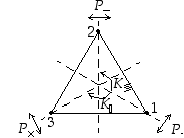V.2.  Tasokuvioiden symmetriaryhmät

Symmetrian kuvaamismallin kehittämiseksi tarkastelemme ensin tasokuvioiden symmetrisyyttä. Ja sitä varten taas tarkastelemme ensin yksinkertaista tasokuviota, tasasivuista kolmiota. Pyrimme kuvaamaan kaikki ne tason symmetriakuvaukset, jotka kuvaavat kolmion takaisin samaksi kolmioksi (mahdollisesti uuteen asentoon). Lisäksi on luonnollista vaatia, että nämä kuvaukset säilyttävät pisteiden etäisyydet.

Numeroidaan kolmion kärjet 1−3 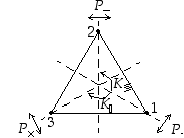ja tarkastellaan sen mahdollisia symmetriakuvauksia, eli kiertoja ja peilauksia. Kolmion eri symmetriakuvaukset ovat selvästikin seuraavat:

• identtinen kuvaus ,

• kierrot ja ,

• peilaukset , ja ,

yhteensä siis kuusi kappaletta. Tarkastelemalla kärkipisteiden kuvautumista huomataan, että jokainen näistä muunnoksista voidaan kuvata permutaatioina. Otetaan käyttöön permutaatiot

, ja ,

jotka vastaavat kuvauksi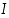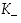a , ja 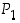. Tässä kierron 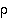suunta on valittu 'paikka-orientoituneesti': luvun 1 kuvautuminen luvuksi 2 tarkoittaa nyt graafisesti sitä, että kolmiota kierretään siten, että kärjen 1 paikalle tulee kärki 2 (tämä sen takia, että permutaatioiden kertomisjärjestys oikealta vasemmalle olisi sopusoinnussa havainnollistamisen kanssa). Permutaatioiden 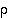ja 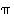tulojen avulla saadaan edelleen, että

Esimerkkinä kuvataan näistä tulon 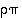muotoutuminen graafisesti (huomaa kierron suunta!).

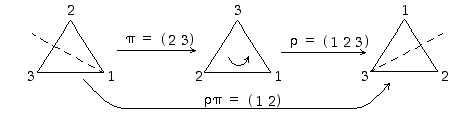
Kaikki mahdolliset symmetriakuvaukset on siten saatu esitettyä permutaatioiden 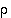ja 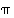avulla. Tuloksena on ns. tasasivuisen kolmion symmetriaryhmä eli dihedraaliryhmä ('tuplatahoryhmä')

Dihedraaliryhmä 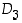on siten aivan sama kuin kolmialkioisen joukon symmetriaryhmä 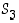. Tarkastelemalla sen alkioiden tuloja voi edelleen helposti laskea, että

,
,
.

Täten kuvauksi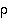a ja 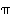kertomalla keskenään ei saada aikaan mitään muita alkioita kuin ne, jotka ovat jo joukossa 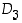. Keräämällä tulokset yhteen saadaan kokoon seuraava taulukko, ryhmän 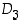operaatiotaulukko. Se on oleellisesti sama kuin ryhmän 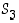operaatiotaulukko (ks. esimerkki 4.1.8), alkiot ovat vain eri nimisiä ja eri järjestyksessä.

Ryhmän 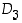alkioiden tuloja laskiessa joudutaan muotoa 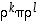oleviin tuloihin. Näitä sieventäessä on kätevää käyttää hyväksi yhtälöit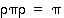ä ja 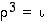. Taulukkoa täyttäessä on myös hyödyllistä muistaa supistamissääntö, jonka mukaan kukin alkio esiintyy kullakin rivillä ja sarakkeella täsmälleen kerran.

Tehtävä. Tarkista ryhmän 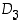operaatiotaulukon kaksi alinta riviä.

Opiskelutehtävä 45. (Kolmion dihedraaliryhmä)

Tarkista ryhmässä 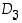tulo 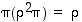graafisesti kolmioiden avulla.

Vinkki tehtävään 45

Tarkastellaan sitten yleisemmin säännöllisen 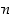−kulmion symmetriaryhmää, kun 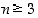. Olkoon 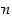ensin pariton, 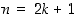. Alla olevasta kuviosta on löydettävissä seuraavat symmetriakuvaukset:

• identtinen kuvaus ,

• kierrot , , …, ,

• peilaukset , , …, ,

yhteensä siis kappaletta.

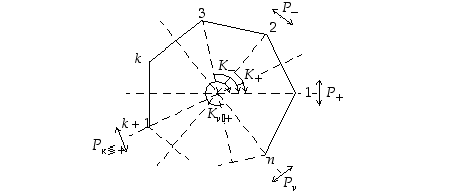
Olkoon 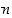sitten parillinen, 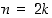. Alla olevasta kuviosta on löydettävissä nyt seuraavat symmetriakuvaukset:

• identtinen kuvaus ,

• kierrot , , …, ,

• peilaukset , , …, ,

• peilaukset , , …, ,

yhteensä siis kappaletta.

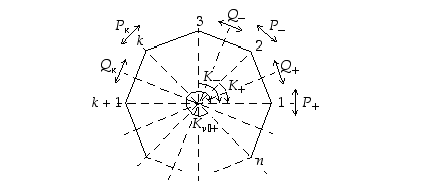
Otetaan kummassakin tapauksessa käyttöön permutaatiot

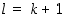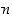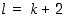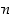missä , jos on pariton, ja , jos on parillinen. Permutaatio 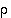vastaa siten kiertoa 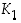ja permutaatio 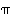peilausta 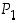. Lasketaan näiden potensseja ja tuloja:

Yhteensä on eri permutaatioita saatu jo 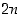kappaletta, ja koska jokainen niistä vastaa eri symmetriakuvausta, olemme jo siis löytäneet kaikki mahdolliset permutaatiot. Näin on muodostettu ns. säännöllisen 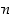−kulmion dihedraaliryhmä

.

Koska jokainen ryhmän 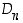alkio on 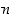alkion permutaatio, on 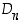ryhmän 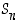aliryhmä. Se ei ole kuitenkaan koko ryhmä, kun 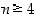, sill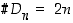ä , mutta .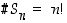

Opiskelutehtävä 46. (Kirjaimen H symmetriaryhmä)

Kuvaa kirjaimen H symmetriaryhmä permutaatioilla ja ilmoita saadun ryhmän kertotaulukko.

Vinkki tehtävään 46

Merkitään dihedraaliryhmän yhden kierron 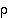potenssien muodostamaa ns. syklistä ryhmää symbolilla 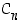, ts.

, (  ).

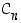on säännöllisen 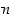−kulmion kiertojen muodostama joukko, sen ns. kiertoryhmä.

Syklisen ryhmän 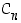alkiolle 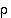pätee, et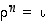tä , mutta 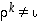, kun 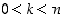. Sanotaan, että tällaisen alkion kertaluku on 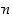. Erikoisesti tällöin 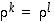täsmälleen silloin, kun 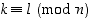. Edelleen pätee, että 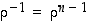, , 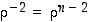jne.

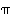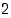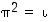Dihedraaliryhmässä vastaavasti peilauksen kertaluku on , ts. , mutta 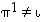. Lisäksi alkioiden 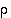ja 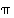tulolle 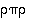pätee:

.

Dihedraaliryhmän 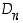kertotaulukko määräytyykin itse asiassa täysin ehdoista

ja .

Esimerkki 5.2.1.

Edellisen pykälän alussa tarkastellussa 12−pyramidissa kierto kulman 30° verran virittää kaikki muut mahdolliset kierrot. Pohjan 12−kulmion peilaukset taas eivät ole enää pyramidin kiertoja. Siten 12−pyramidin ns. kiertoryhmä eli rotaatioryhmä eli se ryhmä, joka muodostuu sen kierroista (ilman peilauksia), on

,

missä 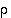on kierto 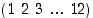, kun 12−kulmion kärjet on numeroitu 1, 2, …, 12.

Esimerkki 5.2.2.

Palataan toiseen edellisen pykälän alussa tarkasteltuun kappaleeseen, 6−prismaan. Sen voidaan ajatella olevan 'kaksitahoinen 6−kulmio', sillä jokainen sen kierto on jokin vastaavan 6−kulmion symmetriamuunnos (kierto tai peilaus), ja kääntäen. Siten 6−prisman kiertoryhmä on dihedraaliryhmä 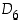. Tämä voidaan kuvata numeroimalla ylä- ja alapuolen vastinkärjet samoin numeroin 1−6 ja valitsemalla esimerkiksi 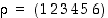ja 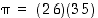. Silloin

ja 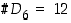. Huomioimalla myös peilaukset saadaan lisää symmetriamuunnoksia. Kuinka paljon? Tuplatenko? Vastataan siihen myöhemmin! (Seuraavassa pykälässä!)

Seuraava tulos annetaan tässä ilman todistusta.

Lause 5.2.3. (Leonardo da Vincin lause)

Tasokuvion äärellinen symmetriaryhmä on oleellisesti jokin syklisistä ryhmistä 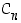tai jokin dihedraaliryhmistä .

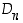Se, mikä symmetriaryhmä kullakin tasokuviolla on, saadaan selville seuraavalla tavalla. Etsitään ensin pienikulmaisin kierto ja määrätään sen kertaluku 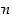. Sitten selvitetään, liittyykö tasokuvioon ylipäätään yhtään peilausta. Jos liittyy, tuloksena on dihedraaliryhmä 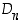− jos ei, tuloksena on syklinen ryhmä .

Esimerkki 5.2.4.

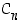Kirjaimella N on symmetriana kierto 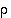, jolle 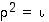, mutta ei yhtään peilausta, joten sen symmetriaryhmä on .

Esimerkki 5.2.5.

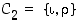Kirjaimella M ei ole yhtään kiertoa, mutta sillä on peilaus, joten sen symmetriaryhmä on .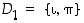

Esimerkki 5.2.6.

Kirjaimella H on symmetriana sekä kierto 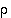, jolle 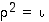, että peilaus, joten sen symmetriaryhmä on .

Esimerkki 5.2.7.

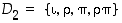Kirjaimella O (ympyränä!) on äärettömän monta kiertoa ja peilausta. Sen symmetriaryhmä ei siksi ole mikään ryhmistä 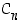tai 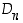. Tästä äärettömästä symmetriaryhmästä käytetään joskus merkintää .

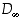Opiskelutehtävä 47. (Kuvioiden symmetriaryhmät)

Määrää alla olevien kuvioiden symmetriaryhmät.

Vinkki tehtävään 47

Harjoitustehtäviä

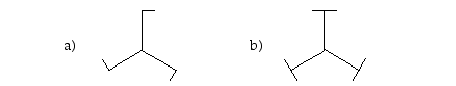
1.   Kuvaa neliön symmetriat ja määrää sen symmetriaryhmä sekä ilmoita sen kertotaulukko. Ilmoita tulos vielä 'dihedraalimaisesti' sopivan ryhmän 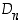avulla.

2.   Kuvaa suorakaiteen (joka ei ole neliö) symmetriat ja määrää sen symmetriaryhmä sekä ilmoita saadun ryhmän kertotaulukko.

3.   Millainen on janan symmetriaryhmä?

4.   Kuvaa säännöllisen viisikulmion symmetriat, määrää sen symmetriaryhmä ja ilmoita saadun ryhmän kertotaulukko.

5.   Kuvaasˇakkilaudan symmetriat ja määrää sen symmetriaryhmä.

6.   Määrää kaikkien ryhmän 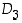alkioiden kertaluvut.

7.   Montako kertalukua 2 olevaa alkiota on neliön symmetriaryhmässä?

8.   Määrää alla olevien kuvioiden symmetriaryhmät.

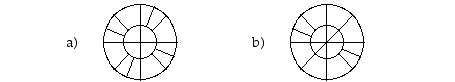
9.   Mikä on seuraavien yhtälöiden määräämien tasokäyrien symmetriaryhmä: a) 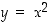  (paraabeli), b) 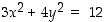(ellipsi), c) 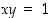(hyperbeli), d) 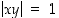(kaksi hyperbeliä)?

10.   Millaisia ryhmiä löytyy kirjainten A−Z symmetriaryhmistä? (Voit olettaa kirjaimet mahdollisimman säännöllisiksi.)

[Ylempi pääsivu] [Edellinen sivu] [Seuraava sivu]