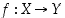 ja
ja 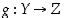 yhdistetty
kuvaus
yhdistetty
kuvaus 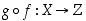 määritellään asettamalla
määritellään asettamalla 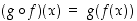 kaikilla
kaikilla 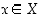 . Joukon
. Joukon 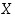 identtinen
kuvaus
identtinen
kuvaus 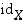 taas määritellään yksinkertaisesti säännöllä
taas määritellään yksinkertaisesti säännöllä 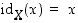 kaikilla
kaikilla 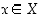 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Kertaamme ensin perusasioita kuvauksista. Kahden kuvauksen 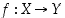 ja
ja 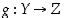 yhdistetty
kuvaus
yhdistetty
kuvaus 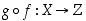 määritellään asettamalla
määritellään asettamalla 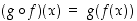 kaikilla
kaikilla 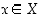 . Joukon
. Joukon 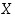 identtinen
kuvaus
identtinen
kuvaus 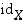 taas määritellään yksinkertaisesti säännöllä
taas määritellään yksinkertaisesti säännöllä 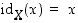 kaikilla
kaikilla 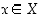 .
.
Kahden joukon välinen kuvaus 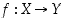 on erikoisesti
injektio,
surjektio tai
bijektio seuraavassa taulukossa esitettyjen määrittelyjen mukaisesti.
on erikoisesti
injektio,
surjektio tai
bijektio seuraavassa taulukossa esitettyjen määrittelyjen mukaisesti.
Bijektiolla 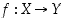 on aina
käänteiskuvaus
on aina
käänteiskuvaus 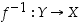 ,
jolle
,
jolle
Nämä ehdot voidaan kirjoittaa myös muotoon
Esimerkiksi alla olevan kuvan mukainen nelialkioisten joukkojen välinen kuvaus on bijektio.
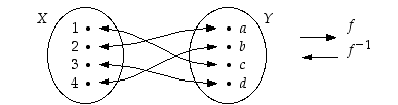
Tarkastelemme jatkossa erityisesti saman joukon  bijektioita
bijektioita  itselleen. Näitä sanotaan, varsinkin äärellisille joukoille
itselleen. Näitä sanotaan, varsinkin äärellisille joukoille 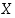 ,
myös
permutaatioiksi. Kiinteälle joukolle
,
myös
permutaatioiksi. Kiinteälle joukolle 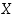 käytämme kaikkien sen bijektioiden joukosta merkintää
käytämme kaikkien sen bijektioiden joukosta merkintää 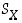 ,
siis
,
siis
Koska bijektioiden yhdistetyt kuvaukset ja niiden käänteiskuvaukset ovat edelleen bijektioita, ovat joukon 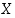 kahden permutaation
kahden permutaation 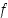 ja
ja 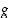 myötä aina permutaatioita myös kuvaukset
myötä aina permutaatioita myös kuvaukset 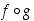 ,
,
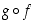 ,
,
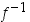 ,
,
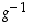 ,
,
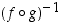 ,
,
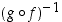 ,
,
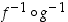 jne. Lisäksi tiedetään, että bijektioille pätee sääntö
jne. Lisäksi tiedetään, että bijektioille pätee sääntö 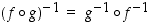 .
.
Erityisesti joukoille 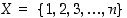 käytetään permutaatioiden muodostamasta joukosta myös merkintää
käytetään permutaatioiden muodostamasta joukosta myös merkintää 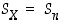 . Tapauksessa
. Tapauksessa 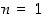 löytyy vain yksi permutaatio, identtinen kuvaus. Siitä syystä oletammekin jatkossa aina, että
löytyy vain yksi permutaatio, identtinen kuvaus. Siitä syystä oletammekin jatkossa aina, että 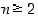 . Näitä joukkoja
. Näitä joukkoja 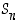 tarkastelemme lähemmin.
tarkastelemme lähemmin.
Määrätään joukon 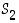 alkiot. Kaksialkioiselle joukolle
alkiot. Kaksialkioiselle joukolle 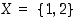 voi löytää vain kaksi bijektiota. Kuvan merkinnöin siis
voi löytää vain kaksi bijektiota. Kuvan merkinnöin siis  .
.
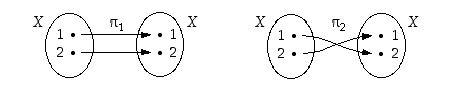
Määrätään joukon  alkiot. Kolmialkioisen joukon
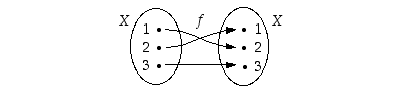
alkiot. Kolmialkioisen joukon 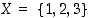 alkiot voi panna eri järjestykseen (permutoida) seuraavasti: 1−2−3, 2−1−3, 3−2−1, 1−3−2, 2−3−1, 3−1−2, yhteensä siis kuudella eri tavalla. Näistä jokainen voidaan ilmoittaa kuvauksena, esimerkiksi tapausta 2−1−3 esittää alla kuvattu kuvaus
alkiot voi panna eri järjestykseen (permutoida) seuraavasti: 1−2−3, 2−1−3, 3−2−1, 1−3−2, 2−3−1, 3−1−2, yhteensä siis kuudella eri tavalla. Näistä jokainen voidaan ilmoittaa kuvauksena, esimerkiksi tapausta 2−1−3 esittää alla kuvattu kuvaus  .
.
Tämä sama riippuvuus ilmoitetaan usein myös vähemmän pystysuunnassa tilaa vievästi kaksirivisenä taulukkona tai 'matriisina' seuraavaan tapaan:
Siinä alarivissä ovat lueteltuina ylärivin alkioiden kuvat: 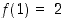 ,
,
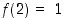 ja
ja 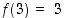 . Tällä tavalla esitettynä joukon
. Tällä tavalla esitettynä joukon 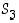 alkiot ovat siten:
alkiot ovat siten:
Yleisemminkin permutaatiota 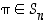 merkitsemme 2−rivisenä taulukkona seuraavasti
merkitsemme 2−rivisenä taulukkona seuraavasti
Tällaisessa esityksessä alkio ja sen kuva-alkio ovat aina allekkain. Näiden parien järjestyksellä ei ole merkitystä, vaikkakin ne usein esitetään ylärivin lukujen pienuusjärjestyksessä. Esimerkiksi kaikki seuraavat matriisit esittävät samaa edellä olevan esimerkin permutaatiota 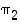 :
:
Koska permutaatiot ovat kuvauksia, ovat kaksi permutaatiota samat, jos ne kuvaavat kaikki alkiot täsmälleen samalla tavalla. Tämän perusteella voimmekin päätellä, montako eri permutaatiota 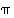 joukossa
joukossa 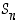 on. Ensinnäkin kuva-alkio
on. Ensinnäkin kuva-alkio 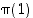 voidaan valita
voidaan valita 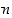 eri tavalla. Koska permutaatioille (eli bijektioille) eri alkioiden pitää kuvautua eri alkioiksi, alkio
eri tavalla. Koska permutaatioille (eli bijektioille) eri alkioiden pitää kuvautua eri alkioiksi, alkio 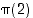 voidaan valita sen jälkeen enää
voidaan valita sen jälkeen enää 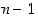 eri tavalla. Näin jatkamalla (ja induktiolla todistamalla) saadaan seuraava tulos.
eri tavalla. Näin jatkamalla (ja induktiolla todistamalla) saadaan seuraava tulos.
Joukossa 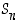 on
on 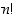 eri alkiota (permutaatiota), ts.
eri alkiota (permutaatiota), ts. 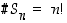 .
.
Lauseessa esiintyvä kertoma 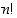 määritellään tulona
määritellään tulona 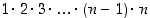 . Tuloksen mukaan
. Tuloksen mukaan 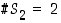 ja
ja 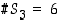 ,
kuten edellä esimerkeissä 4.1.1 ja 4.1.2 todettiinkin. Sen jälkeen mahtavuudet kasvavat nopeasti:
,
kuten edellä esimerkeissä 4.1.1 ja 4.1.2 todettiinkin. Sen jälkeen mahtavuudet kasvavat nopeasti:
Opiskelutehtävä 34. (Permutaatioiden lukumäärä)
(a) Kuinka monta sellaista permutaatiota, jotka kuvaavat alkion 1 itselleen, on ryhmässä 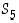 ? Entä sellaista, jotka kuvaavat joko alkiot 1 ja 2 molemmat itselleen tai molemmat toisikseen?
? Entä sellaista, jotka kuvaavat joko alkiot 1 ja 2 molemmat itselleen tai molemmat toisikseen?
(b) Yleistyksenä ilmoita edelleen, kuinka monta sellaista permutaatiota, jotka kuvaavat
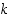 ensimmäistä alkiota kaikki itselleen, on ryhmässä
ensimmäistä alkiota kaikki itselleen, on ryhmässä 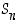 ? Entä sellaista, jotka kuvaavat ne keskenään joko itselleen tai toisikseen?
? Entä sellaista, jotka kuvaavat ne keskenään joko itselleen tai toisikseen?
Permutaatioita voidaan tietenkin yhdistää kuten kuvauksiakin. Usein vain kuvausten yhdistämistä osoittava pallomerkintä jätetään pois ja sen sijasta käytetään pelkkää tulomerkintää (ilman mitään välimerkkiä).
tulot (esimerkin 4.1.2 merkintöjä käyttäen). Näiden yhdistetylle kuvaukselle on
Sama nähdään myös graafisesti:
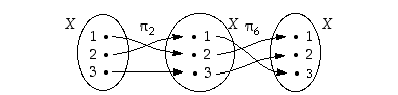
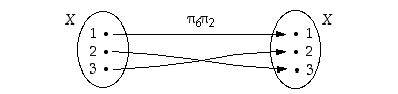
Vastaavasti samat permutaatiot toisinpäin kerrottuna antavat tuloksen
Huomaa erityisesti, että permutaatiot kerrotaan, kuten kuvaukset yhdistetään, oikealta vasemmalle: ensin siis katsotaan, mitä oikeanpuoleinen kuvaus tekee kullekin alkiolle, ja sitten, mitä vasemmanpuoleinen tekee niille sen jälkeen. Esimerkiksi yllä viimeisimmässä yhtälössä 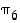 kuvaa alkion 3 ensin alkioksi 2 ja
kuvaa alkion 3 ensin alkioksi 2 ja 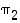 sitten alkion 2 alkioksi 1; yhdistettynä siis alkio 3 kuvautuu alkioksi 1.
sitten alkion 2 alkioksi 1; yhdistettynä siis alkio 3 kuvautuu alkioksi 1.
Huomaa myös, että kertolasku voi antaa eri tuloksen kertomisjärjestyksestä riippuen. Näin tapahtuikin yllä esimerkissä 4.1.4, jossa siis
Permutaation
käänteispermutaatio (käänteiskuvaus) näkyy helposti matriisiesityksestä: riittää vain vaihtaa ylä- ja alarivit keskenään (jonka jälkeen kuvausparit voi järjestää ylärivin mukaan pienuusjärjestykseen). Tämä perustuu yksinkertaisesti siihen, että permutaatiolle 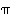 on
on 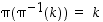 ja
ja 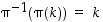 .
.
Muodostetaan joukon 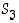 alkion
alkion 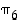 (ks. esimerkki 4.1.2) käänteispermutaatio:
(ks. esimerkki 4.1.2) käänteispermutaatio:
Opiskelutehtävä 35. (Permutaatioiden tulo ja käänteispermutaatiot)
tulot 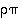 ja
ja 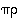 sekä käänteispermutaatiot
sekä käänteispermutaatiot 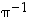 ja
ja 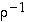 .
.
Opiskelutehtävä 36. (Kolmen alkion permutaatioiden tulot)
Käyttäen esimerkin 4.1.2 merkintöjä määrää joukon 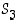 alkioille permutaatiot
alkioille permutaatiot 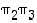 ,
,
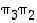 ,
,
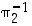 ,
,
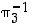 ,
,
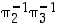 ,
,
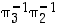 ,
,
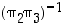 ja
ja 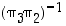 . Selvitä kussakin tapauksessa, mikä joukon
. Selvitä kussakin tapauksessa, mikä joukon 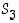 alkio tulee vastaukseksi. Vertaa myös eri tuloksia keskenään. Tunnistatko mitään sääntöjä?
alkio tulee vastaukseksi. Vertaa myös eri tuloksia keskenään. Tunnistatko mitään sääntöjä?
Joukon 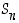 kaikille alkioille
kaikille alkioille 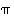 ,
,
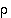 ja
ja 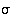 pätevät seuraavat:
pätevät seuraavat:
(c)  ,
kun
,
kun 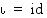 on identtinen kuvaus,
on identtinen kuvaus,
Kaikki kyseiset ominaisuudet seuraavat suoraan kuvausten ja bijektioiden ominaisuuksista.
Yllä olevassa lauseessa kohdan (b) ominaisuutta voi sanoa
sulkujen
poistoluvaksi,
sillä sen mukaan tulo 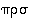 on riippumaton ryhmittelyjärjestyksestä eikä siinä siten tarvita sulkuja osoittamaan sitä. Kertomisjärjestyksellä on sen sijaan merkitystä.
on riippumaton ryhmittelyjärjestyksestä eikä siinä siten tarvita sulkuja osoittamaan sitä. Kertomisjärjestyksellä on sen sijaan merkitystä.
Joukko 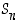 varustettuna yllämainituilla alkioiden yhdistelyominaisuuksilla on taasen esimerkki eräästä yleisemmästä algebrallisesta struktuurista, nimittäin
ryhmästä. Joukkoa
varustettuna yllämainituilla alkioiden yhdistelyominaisuuksilla on taasen esimerkki eräästä yleisemmästä algebrallisesta struktuurista, nimittäin
ryhmästä. Joukkoa 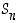 sanotaankin
astetta
sanotaankin
astetta 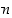 olevaksi
symmetriseksi
ryhmäksi. Symmetria-sanan esiintyminen nimessä selittyy myöhemmin luvussa Symmetria, kun tarkastelemme lähemmin tasokuvioiden ja avaruuskappaleiden symmetrisyyttä. Osoittautuu nimittäin, että näiden symmetrian kuvaamiseen voidaan käyttää ryhmiä
olevaksi
symmetriseksi
ryhmäksi. Symmetria-sanan esiintyminen nimessä selittyy myöhemmin luvussa Symmetria, kun tarkastelemme lähemmin tasokuvioiden ja avaruuskappaleiden symmetrisyyttä. Osoittautuu nimittäin, että näiden symmetrian kuvaamiseen voidaan käyttää ryhmiä 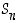 .
.
Ryhmän 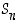 alkioiden tulot ovat siis aina edelleen sen alkioita. Kun aste
alkioiden tulot ovat siis aina edelleen sen alkioita. Kun aste 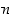 on pieni, voidaan kertomisen tulokset esittää
kertolasku- eli
operaatiotaulukon avulla. Seuraavissa esimerkeissä tämä tehdään, kun
on pieni, voidaan kertomisen tulokset esittää
kertolasku- eli
operaatiotaulukon avulla. Seuraavissa esimerkeissä tämä tehdään, kun 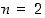 ja
ja 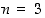 .
.
jolloin 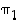 on identtinen kuvaus ja
on identtinen kuvaus ja 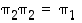 . Näillä tiedoilla saadaan seuraava kertotaulukko:
. Näillä tiedoilla saadaan seuraava kertotaulukko:
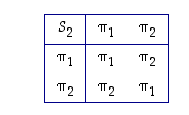
Merkitään ryhmän 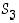 alkioita esimerkin 4.1.2 mukaisesti
alkioita esimerkin 4.1.2 mukaisesti
Esimerkissä 4.1.4 on laskettu, että 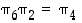 ja
ja 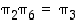 . Kun lasketaan vastaavasti kaikki muut tulot, saadaan seuraava operaatiotaulukko:
. Kun lasketaan vastaavasti kaikki muut tulot, saadaan seuraava operaatiotaulukko:

Opiskelutehtävä 37. ((Kolmen alkion permutaatioiden kertotaulukko)
Tarkista ryhmän 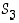 kertotaulukon jotkin kaksi riviä tai saraketta (mutta ei kahta ensimmäistä) oikeiksi.
kertotaulukon jotkin kaksi riviä tai saraketta (mutta ei kahta ensimmäistä) oikeiksi.
Renkaassa 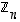 yhtälöä
yhtälöä 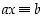 ei voitu aina ratkaista. Ryhmässä
ei voitu aina ratkaista. Ryhmässä 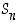 voidaan kuitenkin aina tämäntyyppiset yhtälöt
voidaan kuitenkin aina tämäntyyppiset yhtälöt 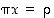 ratkaista.
ratkaista.
Ryhmässä 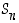 yhtälöllä
yhtälöllä 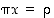 on yksikäsitteinen ratkaisu
on yksikäsitteinen ratkaisu 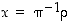 . Vastaavasti yhtälöllä
. Vastaavasti yhtälöllä 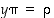 on yksikäsitteinen ratkaisu
on yksikäsitteinen ratkaisu 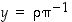 .
.
joten ne ovat väitettyjen yhtälöiden ratkaisuja. Se, että nämä ovat ainoat ratkaisut, nähdään taas heti, kun kerrotaan ratkaistavat yhtälöt alkiolla 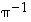 ,
edellinen vasemmalta ja jälkimmäinen oikealta.
,
edellinen vasemmalta ja jälkimmäinen oikealta.
Yhtälöiden 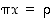 ja
ja 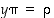 ratkaiseminen tapahtuu siis kertomalla yhtälöt kertoimen
ratkaiseminen tapahtuu siis kertomalla yhtälöt kertoimen 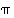 käänteispermutaatiolla
käänteispermutaatiolla 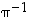 siltä samalta puolelta, jolla kerroin on ratkaistavan muuttujan suhteen.
siltä samalta puolelta, jolla kerroin on ratkaistavan muuttujan suhteen.
Ryhmässä 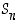 pätee ns. supistamissääntö: jos
pätee ns. supistamissääntö: jos 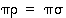 ,
niin välttämättä
,
niin välttämättä 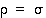 ,
ja vastaavasti, jos
,
ja vastaavasti, jos 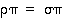 ,
niin
,
niin 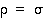 .
.
Todistus. Yhtälöstä 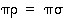 seuraa edellisen lauseen perusteella, että
seuraa edellisen lauseen perusteella, että
Vastaavasti ehdosta 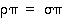 seuraa, että
seuraa, että
Supistamissääntö on hyödyllistä muistaa silloin, kun laaditaan ryhmille 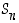 kertolaskutaulukoita. Tämän säännön mukaan nimittäin tällaisessa taulukossa kukin ryhmän alkio esiintyy kullakin rivillä ja sarakkeella korkeintaan yhden kerran. Toisaalta paikkoja on yhtä monta kuin käytettäviä alkioita, joten itse asiassa kukin ryhmän alkio esiintyy kullakin rivillä ja sarakkeella täsmälleen kerran.
kertolaskutaulukoita. Tämän säännön mukaan nimittäin tällaisessa taulukossa kukin ryhmän alkio esiintyy kullakin rivillä ja sarakkeella korkeintaan yhden kerran. Toisaalta paikkoja on yhtä monta kuin käytettäviä alkioita, joten itse asiassa kukin ryhmän alkio esiintyy kullakin rivillä ja sarakkeella täsmälleen kerran.
sen potensseja. Laske siis potensseja 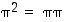 ,
,
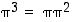 ,
…, sekä myös potensseja
,
…, sekä myös potensseja 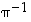 ,
,
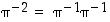 ,
,
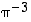 ,
…. Päättele sääntö, jonka avulla voit ilmoittaa minkä tahansa potenssin
,
…. Päättele sääntö, jonka avulla voit ilmoittaa minkä tahansa potenssin 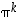 .
.
Ratkaise 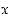 ,
,
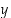 ja
ja 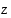 yhtälöistä
yhtälöistä 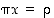 ,
,
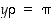 ja
ja 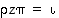 .
.
3. Osoita, että ryhmässä 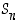 ehdosta
ehdosta 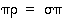 ei voi päätellä aina, että
ei voi päätellä aina, että 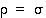 . (Vihje: Etsi ensin ryhmästä
. (Vihje: Etsi ensin ryhmästä 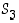 sopiva vastaesimerkki ja yleistä se sitten).
sopiva vastaesimerkki ja yleistä se sitten).