[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Jokaisella lienee valmiina jonkinlainen mielikuva siitä, mitä symmetrisyys ja symmetria tarkoittavat. Mutta miten ilmoittaa täsmällisemmin, kuinka symmetrinen joku kuvio tai kappale on? Tai voiko sanoa, mikä annetuista kuvioista tai kappaleista on symmetrisin?
Tarkastellaan ensin kolmea avaruuskappaletta: 12−pyramidia, 6−prismaa ja 4−tahokasta eli tetraedria. Oletetaan kaikkien kappaleiden pohjana olevat monikulmiot säännöllisiksi.

Tehtävä. Mikä näistä kappaleista on mielestäsi symmetrisin? Mihin arviosi perustuu? Löydätkö päättelysi tueksi jotain rationaalista mallia, jota voisi yleisemminkin soveltaa?
Todennäköisesti löydät symmetriaa kahdella tavalla. On helppo havaita tasokuvioissa peilisymmetriaa, kuten alla olevassa sydänkuviossa, ja usein myös kiertosymmetriaa, kuten esimerkiksi kirjaimessa N. Edellisessä tapauksessa kuviosta löytyy suora, peilausakseli, jonka suhteen kuvio on itsensä peilikuva. Jälkimmäisessä tapauksessa taas on yksi piste, kiertokeskus, jonka suhteen kiertämällä kuvio yhtyy (ennen täyttä kierrosta) alkuperäiseen muotoonsa.

Peilisymmetriaa voi periaatteessa esiintyä myös yhden pisteen suhteen (tähtimäisesti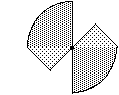 ), mutta se voidaan kuvata peilausakselien tai kiertokeskusten avulla, kuten esimerkiksi viereisen kuvion tapauksessa.
), mutta se voidaan kuvata peilausakselien tai kiertokeskusten avulla, kuten esimerkiksi viereisen kuvion tapauksessa.
Avaruuskappaleissa peilausakselin tilalla on ilmeisestikin peilaustaso ja kiertokeskuksen tilalla kiertoakseli. Lisäksi avaruuskappaleissakin voi periaatteessa olla peilisymmetriaa suoran tai pisteen suhteen.
Palataan alussa tarkasteltuihin kolmeen avaruuskappaleeseen. Niiden symmetrisyyttä voisi siis yrittää kuvata etsimällä kaikki mahdolliset peilaustasot ja kiertosuorat. On siis yritettävä vastata seuraaviin kahteen kysymykseen:
• Kuinka monella oleellisesti eri tavalla kappaletta voi kiertää siten, että uudessa asennossa kappaletta ei voi erottaa alkuperäisessä asennossa olevasta (muuten kuin nimeämällä alunpitäen jotkin kappaleen osat, kuten esimerkiksi kärkipisteet)?
• Kuinka monta eri peilikuvaansa kappaleella on?
Tarkastellaan kutakin kappaletta erikseen.
Esimerkki 5.1.1. (12−pyramidi)
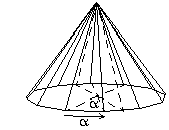 Pyramidia voidaan kiertää lähtöasennosta pystyakselinsa suhteen 11 eri tavalla (kun täyttä kiertoa ei enää oteta mukaan). Pienin kierto on kulman
Pyramidia voidaan kiertää lähtöasennosta pystyakselinsa suhteen 11 eri tavalla (kun täyttä kiertoa ei enää oteta mukaan). Pienin kierto on kulman
verran, ja muut ovat sen toistoja eli monikertoja.
Peilauksia löytyy yhteensä 12 kappaletta; peilaustasoina ovat sellaiset tasot, jotka kulkevat huippupisteen kautta ja sisältävät joko 12−kulmion kaksi vastakkaista kärkeä tai kahden vastakkaisen sivun keskipisteet.
• 11 kiertoa kulman 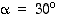 monikertojen verran ja
monikertojen verran ja
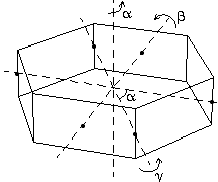 Kiertoja löytyy nyt kolmenlaisten suorien suhteen: kappaleen pystyakselin, vastakkaisten sivutahkojen keskipisteiden kautta kulkevan ja vastakkaisten sivusärmien keskipisteiden kautta kulkevan.
Kiertoja löytyy nyt kolmenlaisten suorien suhteen: kappaleen pystyakselin, vastakkaisten sivutahkojen keskipisteiden kautta kulkevan ja vastakkaisten sivusärmien keskipisteiden kautta kulkevan.
Pystyakselin suhteen pienin kierto on kulman
verran ja sen monikertoina saadaan neljä kiertoa lisää (täysi kierros poisluettuna).
Vastakkaisia sivutahkoja yhdistävän suoran suhteen saadaan yksi kierto lisää, kulman 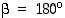 verran. Eri sivutahkopareja taas on kolme kappaletta, joten yhteensä saadaan kolme kiertoa lisää. Vastaavasti sivusärmien suhteen saadaan kolme kiertoa lisää, ja kukin niistä kiertää prismaa kulman
verran. Eri sivutahkopareja taas on kolme kappaletta, joten yhteensä saadaan kolme kiertoa lisää. Vastaavasti sivusärmien suhteen saadaan kolme kiertoa lisää, ja kukin niistä kiertää prismaa kulman 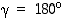 verran.
verran.
Kaikkiaan löytyy siis 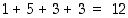 eri kiertoa.
eri kiertoa.
Peilauksia löytyy 6−prismasta kaikkiaan 7 kappaletta. Peilaustasoina ovat eri kiertoakseliparien määräämät tasot.
Yhteensä siis 6−prismasta löytyy:
• 5 eri kiertoa kulman 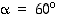 monikertojen verran,
monikertojen verran,
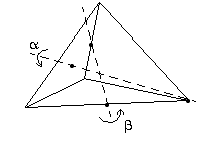 Kiertoja löytyy nyt kahdenlaisten suorien suhteen: Yhdestä kärjestä katsottuna tetraedrin vastakkaista tahkoa voi kiertää kulman
Kiertoja löytyy nyt kahdenlaisten suorien suhteen: Yhdestä kärjestä katsottuna tetraedrin vastakkaista tahkoa voi kiertää kulman
verran ja sen monikertana saadaan yksi kierto lisää (täysi kierros poisluettuna). Tällaisia kiertoja on kaikkiaan neljän eri kärjen suhteen yhteensä kahdeksan kappaletta. Yhdistämällä sitten aina vastakkaisten särmien keskipisteet saadaan lisää kolme uutta kiertoa, kukin kulman 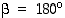 verran.
verran.
Peilauksia löytyy tetraedrista kaikkiaan vain 6 kappaletta.
Yhteensä siis tetraedrista löytyy:
• 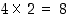 eri kiertoa kulman
eri kiertoa kulman 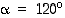 monikertojen verran,
monikertojen verran,
Opiskelutehtävä 44. (Kuution kiertosymmetriat)
Kuvaa kaikki kuution erilaiset kiertosymmetriat ja määrää näiden kokonaismäärä.
Seuraavassa on näistä kolmesta esimerkistä yhteenvetona eräitä huomioita, joilla voisi olla merkitystä kappaleiden symmetrisyyden kuvaamisessa:
• Kaikilla kolmella kappaleella on yhteensä 12 erilaista kiertosymmetriaa.
• Pyramidilla on vain yksi kiertoakseli, prismalla ja tetraedrilla niitä on kummallakin kaikkiaan seitsemän erilaista.
• Pyramidilla yhden kierron toistaminen antaa kaikki muut sen monikertoina, mutta prismalla ja tetraedrilla ei tällaista kiertoa löydy.
• Pyramidilla kaksi kiertoa voidaan aina toistaa missä järjestyksessä tahansa, mutta prismalla ja tetraedrilla kiertojen suoritusjärjestyksellä on merkitystä. (Prismalla epävaihdannaisia kiertopareja löytyy 30 ja tetraedrilla 29.)
• Pyramidilla on vain yksi sellainen kierto (kulman 180° verran), joka yhden kerran toistettuna antaa alkuperäisen asennon, prismalla niitä on kaikkiaan seitsemän erilaista ja tetraedrilla vastaavasti kolme.
• Pyramidilla ja prismalla on kaksi sellaista kiertoa (kulmien 120° ja 240° verran), jotka toistettuna kahdesti antavat alkuperäisen asennon, tetraedrilla niitä on vastaavasti kahdeksan.
• Erilaisia peilaustasoja on pyramidilla yhteensä 12, prismalla 7 ja tetraedrilla 6.
Yleisesti tunnutaan oleva sitä mieltä, että näistä kolmesta esimerkkikappaleesta pyramidilla on vähiten sisäistä symmetriaa. Prisman ja tetraedrin välillä mielipiteet jo jonkun verran vaihtelevat, mutta enemmistö kallistuu yleensä sille kannalle, että tetraedri olisi symmetrisempi kappale kuin prisma. Mitkä yllä luetellut näiden kappaleiden ominaisuudet sitten tukisivat tällaista tuntumaa?
Teemme esimerkkien pohjalta seuraavan hypoteesin:
• Enemmän kiertoja omaava kuvio tai kappale on symmetrisempi.
• Enemmän kiertoakseleita omaava kuvio tai kappale on symmetrisempi.
• Enemmän epävaihdannaisia kiertoja omaava kuvio tai kappale on symmetrisempi.
• Enemmän isokulmaisia kiertoja omaava kuvio tai kappale on symmetrisempi.
Voisimme siis ilmeisesti sanoa, että mitä enemmän kappaleella on kiertoja, ja ennen kaikkea mitä pahemmin ne ovat sekoittuneet keskenään, sitä symmetrisempi kappale on!
Kun symmetriaa alunpitäen pohditaan, usein ensivaikutelmana korostetaan peilauksien määrää symmetrian mittarina. Yllä olevat esimerkit kuitenkin osoittavat, ettei ainakaan näiden lukumäärä kuvaa kappaleiden symmetriaa. Ehkä päinvastoin niiden vähyys! Jatkossa osoitammekin, että matemaattisesti selkeämpää on ensin tarkastella mahdollisia kiertoja ja niiden keskinäistä käyttäytymistä. Sen jälkeen riittää vain tutkia, onko kappaleella ylipäätään yhtään peilausta. Jos on, riittää näistä ottaa tarkasteluihin mukaan vain yksi − muut mahdolliset peilaukset saadaan tämän yhden peilauksen ja kiertojen avulla.
1. Liimaa kaksi tetraedria yhdestä tahostaan yhteen. Kuvaa saadun (epäsäännöllisen) 6−tahokkaan kaikki kiertosymmetriat.
2. Tarkastele vierekkäistä 'viivoitettua' kuutiota.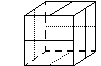 Mitkä kuution kierrot kuvaavat sen niin, että viivat tulevat samoihin asentoihin?
Mitkä kuution kierrot kuvaavat sen niin, että viivat tulevat samoihin asentoihin?