IV.3. Parillisuus ja parittomuus
Edellisen pykälän lauseen 4.2.6 mukaan jokainen permutaatio 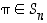 voidaan esittää vaihtojen tulona. Tällainen esitys ei ole kuitenkaan yksikäsitteinen, koska aina voidaan mihin tahansa esitykseen lisätä esimerkiksi tulopari
voidaan esittää vaihtojen tulona. Tällainen esitys ei ole kuitenkaan yksikäsitteinen, koska aina voidaan mihin tahansa esitykseen lisätä esimerkiksi tulopari 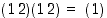 . Tällöin kuitenkin lisätään kaksi vaihtoa, ja yleisemmin osoittautuukin, että vaihtoja voidaan lisätä tai vähentää aina vain parillinen määrä. Perustellaan se seuraavaksi. Avuksi tarvitsemme ensin paria apulausetta.
. Tällöin kuitenkin lisätään kaksi vaihtoa, ja yleisemmin osoittautuukin, että vaihtoja voidaan lisätä tai vähentää aina vain parillinen määrä. Perustellaan se seuraavaksi. Avuksi tarvitsemme ensin paria apulausetta.
Apulause 4.3.1.
Olkoot 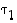 ja
ja 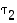 eri vaihtoja, joista
eri vaihtoja, joista 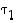 vaihtaa luvun
vaihtaa luvun 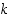 (ts.
(ts. 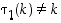 ). Silloin tulo
). Silloin tulo 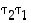 voidaan esittää kahden sellaisen vaihdon
voidaan esittää kahden sellaisen vaihdon 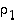 ja
ja 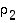 tulona,
tulona, 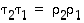 ,
joista vaihto
,
joista vaihto 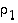 ei vaihda lukua
ei vaihda lukua 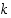 miksikään, mutta
miksikään, mutta 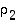 vaihtaa sen (ts.
vaihtaa sen (ts. 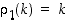 ,
mutta
,
mutta 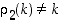 ).
).
Todistus. Merkintöjen yksinkertaistamiseksi oletetaan ensin, että 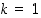 ja
ja 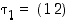 . Silloin on oleellisesti seuraavat kolme mahdollisuutta:
. Silloin on oleellisesti seuraavat kolme mahdollisuutta:
(1) Jos 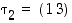 ,
niin
,
niin 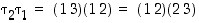 .
.
(2) Jos 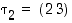 ,
niin
,
niin 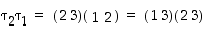 .
.
(3) Jos 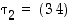 ,
niin
,
niin 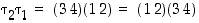 .
.
Jokaisessa tapauksessa on siis saatu väitetynlainen esitys. Koska yllä lukujen 1, 2, 3 ja 4 tilalla voivat esiintyä mitkä tahansa eri luvut, kattavat yllä käsitellyt tapaukset kaikki mahdollisuudet.

Apulause 4.3.2.
Jos identtinen permutaatio 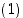 voidaan esittää tulona, jossa on
voidaan esittää tulona, jossa on 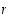 vaihtoa, ja jos
vaihtoa, ja jos 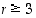 ,
voidaan
,
voidaan 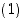 esittää tulona, jossa on vain
esittää tulona, jossa on vain 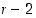 vaihtoa.
vaihtoa.
Todistus. Olkoon identtisellä permutaatiolla seuraavanlainen esitys vaihtojen tulona:
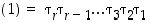 .
.
Jos 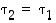 ,
on
,
on 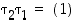 ja tämä tulo voidaan permutaation
ja tämä tulo voidaan permutaation 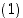 esityksestä poistaa, jolloin saadaan vaadittu lyhyempi esitys.
esityksestä poistaa, jolloin saadaan vaadittu lyhyempi esitys.
Oletetaan sitten, että 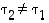 . Merkitään, että
. Merkitään, että 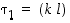 ,
missä
,
missä 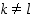 . Koska
. Koska 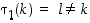 ,
on apulauseen 4.3.1 mukaan
,
on apulauseen 4.3.1 mukaan 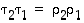 ,
missä
,
missä 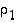 ja
ja 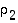 ovat sellaisia vaihtoja, että
ovat sellaisia vaihtoja, että 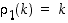 ja
ja 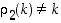 . Siten
. Siten
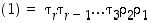 .
.
Jos tässä esityksessä 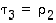 ,
voidaan tulo
,
voidaan tulo 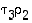 taas poistaa, jolloin saadaan vaadittu lyhyempi esitys.
taas poistaa, jolloin saadaan vaadittu lyhyempi esitys.
Jos 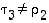 ,
löytyvät samoin kuin edellä vaihdot
,
löytyvät samoin kuin edellä vaihdot 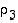 ja
ja 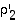 siten, että
siten, että 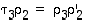 ,
,
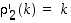 ja
ja 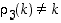 . Näin jatketaan.
. Näin jatketaan.
Jos sitten missään vaiheessa ei voitaisi supistaa kahta vierekkäistä vaihtoa pois, saataisiin tilanne, jossa
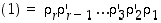 ,
,
ja 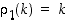 ,
,
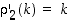 ,
,
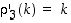 ,
…,
,
…, 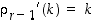 ,
mutta
,
mutta 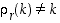 . Edelleen saataisiin, että
. Edelleen saataisiin, että
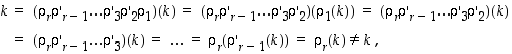
mikä on tietenkin ristiriita. Jossain vaiheessa siis kyseistä identtisen permutaation esitystä voidaan lyhentää kahdella vaihdolla, kuten väitettiinkin.

Näiden kahden apulauseen jälkeen voidaan todistaa varsinainen päätulos.
Lause 4.3.3.
Missä tahansa permutaation 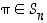 esityksessä vaihtojen tulona on joko aina parillinen tai aina pariton määrä vaihtoja.
esityksessä vaihtojen tulona on joko aina parillinen tai aina pariton määrä vaihtoja.
Todistus. Olkoon permutaatiolla 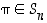 seuraavat esitykset vaihtojen tulona:
seuraavat esitykset vaihtojen tulona:
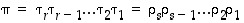 .
.
Kertomalla tämä yhtälö vuoronperään oikealta vaihdon 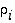 käänteisvaihdolla ja huomioimalla lopuksi, että se on sama vaihto
käänteisvaihdolla ja huomioimalla lopuksi, että se on sama vaihto 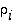 ,
saadaan seuraava päättelyketju:
,
saadaan seuraava päättelyketju:
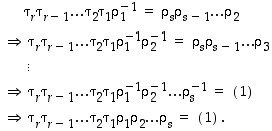
Siten identtinen permutaatio on saatu esitettyä 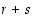 vaihdon tulona. Lauseen väitteen todistamiseksi riittää tämän jälkeen osoittaa, että
vaihdon tulona. Lauseen väitteen todistamiseksi riittää tämän jälkeen osoittaa, että 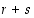 on parillinen.
on parillinen.
Jos luku 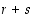 olisi pariton, voisi apulauseen 4.3.2 mukaan identtisen permutaation
olisi pariton, voisi apulauseen 4.3.2 mukaan identtisen permutaation 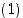 esitystä lyhentää ensin
esitystä lyhentää ensin 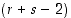 −pituiseksi, sitten
−pituiseksi, sitten 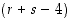 −pituiseksi, jne, kunnes saataisiin jokin 1−pituinen esitys
−pituiseksi, jne, kunnes saataisiin jokin 1−pituinen esitys 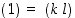 . Mutta tämä ei selvästikään ole mahdollista. Siten luku
. Mutta tämä ei selvästikään ole mahdollista. Siten luku 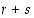 ja sen myötä myös
ja sen myötä myös 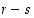 on parillinen eli joko molemmat luvuista
on parillinen eli joko molemmat luvuista 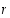 ja
ja 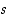 ovat parillisia tai sitten molemmat ovat parittomia. Lauseen väite on todistettu.
ovat parillisia tai sitten molemmat ovat parittomia. Lauseen väite on todistettu.

Permutaation 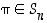 sanotaankin olevan
parillinen tai
pariton sen mukaan tarvitaanko sen tuloesitykseen parillinen vai pariton määrä vaihtoja. Sanotaan myös, että sen
merkki
sanotaankin olevan
parillinen tai
pariton sen mukaan tarvitaanko sen tuloesitykseen parillinen vai pariton määrä vaihtoja. Sanotaan myös, että sen
merkki 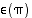 on
on 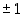 ; parilliselle
; parilliselle 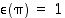 ja parittomalle
ja parittomalle 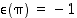 .
.
On helppo huomata, että kahden parillisen tai kahden parittoman permutaation tulo on parillinen, kun taas parittoman ja parillisen permutaation tulo on pariton. Toisin sanoen permutaatiotulon 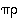 merkki saadaan tekijöiden
merkki saadaan tekijöiden 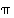 ja
ja 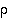 merkkien tulona eli
merkkien tulona eli
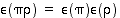 .
.
Tämän säännön voi selvästi yleistää usean permutaation tuloille.
Kuten edellisessä pykälässä Permutaatioesityksiä todettiin, voidaan kierrot esittää vaihtojen tulona seuraavasti:
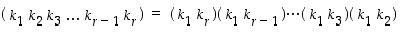 .
.
Tässä esityksessä on 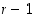 vaihtoa, joten näemme, että
vaihtoa, joten näemme, että 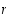 −kierto on parillinen, mikäli sen pituus
−kierto on parillinen, mikäli sen pituus  on pariton, ja pariton, mikäli
on pariton, ja pariton, mikäli 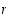 on parillinen. Toisin sanoen, kierron merkki saadaan kaavasta
on parillinen. Toisin sanoen, kierron merkki saadaan kaavasta
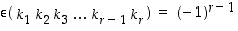 .
.
Koska jokainen permutaatio voitiin edelleen esittää erillisten kiertojen tulona, sen merkki saadaan selville tuloesityksessä olevien kiertojen pituuksien avulla.
Esimerkki 4.3.4.
Permutaatio
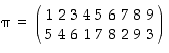
voidaan esittää kiertojen tulona seuraavasti:
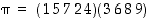 .
.
Koska vasemmanpuoleinen kierto on parillinen (sen pituus on 5 ) ja oikeanpuoleinen kierto on pariton (sen pituus on 4 ), on 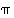 näiden tulona pariton. Sama päätelmä voidaan tehdä myös merkistä
näiden tulona pariton. Sama päätelmä voidaan tehdä myös merkistä
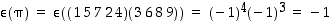 .
.

Opiskelutehtävä 41. (Permutaatiot vaihtojen tulona)
Ilmoita edellisen pykälän (Permutaatioesityksiä) harjoitustehtävien 1 ja 2 permutaatiot
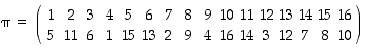
ja 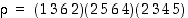 vaihtojen tulona. Ovatko ne parillisia vai parittomia?
vaihtojen tulona. Ovatko ne parillisia vai parittomia?
Vinkki tehtävään 41
Tarkastelemme lähemmin parillisten permutaatioiden muodostamaa joukkoa
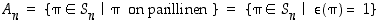 .
.
Sen alkioilla on mm. seuraavat ominaisuudet.
Lause 4.3.5.
Joukon 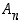 alkioille pätee:
alkioille pätee:
(a) 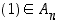 ,
,
(b) jos 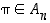 ,
niin myös
,
niin myös 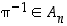 ,
,
(c) jos 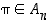 ja
ja 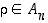 ,
niin myös
,
niin myös 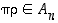 .
.
Todistus. (a) Koska 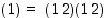 ,
on
,
on 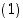 parillinen.
parillinen.
(b) Jos parillisille permutaatioille 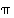 olisi käänteispermutaatio
olisi käänteispermutaatio 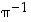 pariton, olisi niiden tulo
pariton, olisi niiden tulo 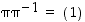 pariton vastoin edellisen kohdan tulosta.
pariton vastoin edellisen kohdan tulosta.
(c) Parillisille permutaatioille 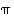 ja
ja 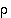 merkit ovat
merkit ovat 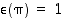 ja
ja 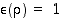 ,
joten
,
joten 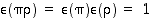 eli
eli 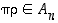 .
.

Algebrallisesti yllä oleva lause ilmaisee, että joukko 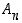 on ryhmän
on ryhmän 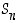 aliryhmä. Tämä tarkoittaa erityisesti sitä, että se on myös ryhmä, ts. sillä on samat lauseen 4.1.6 ominaisuudet kuin ryhmällä
aliryhmä. Tämä tarkoittaa erityisesti sitä, että se on myös ryhmä, ts. sillä on samat lauseen 4.1.6 ominaisuudet kuin ryhmällä 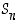 . Ryhmää
. Ryhmää 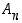 sanotaan
astetta
sanotaan
astetta 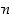 olevaksi
alternoivaksi ryhmäksi.
olevaksi
alternoivaksi ryhmäksi.
Osoitamme seuraavaksi, että parillisia ja parittomia permutaatioita on yhtä paljon, kumpiakin sen mukaisesti puolet ryhmän 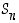 alkioista.
alkioista.
Lause 4.3.6.
Ryhmässä 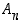 on
on 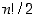 eri alkiota.
eri alkiota.
Todistus. Merkitään parittomien permutaatioiden muodostamaa joukkoa
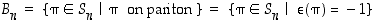 .
.
Koska permutaatio on joko parillinen tai pariton, joukoille 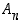 ja
ja 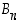 on
on
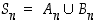 ja
ja 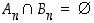 .
.
Jos sitten kerromme parillisen permutaation vaihdolla 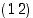 ,
saamme tulokseksi parittoman permutaation. Voimme siis määritellä kuvauksen
,
saamme tulokseksi parittoman permutaation. Voimme siis määritellä kuvauksen 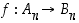 asettamalla
asettamalla 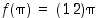 . Osoitamme, että tämä kuvaus on bijektio.
. Osoitamme, että tämä kuvaus on bijektio.
Ensinnäkin, ehdosta 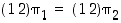 saadaan
saadaan 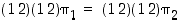 eli
eli 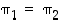 . Kuvaus
. Kuvaus 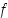 on siten injektio. Toisaalta jokaiselle parittomalle
on siten injektio. Toisaalta jokaiselle parittomalle 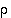 on permutaatio
on permutaatio 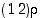 parillinen ja
parillinen ja 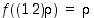 . Kuvaus
. Kuvaus 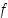 on siten myös surjektio.
on siten myös surjektio.
Joukot 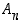 ja
ja 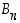 ovat siis yhtä mahtavat eli niissä on yhtä monta alkiota. Koska niissä on yhteensä
ovat siis yhtä mahtavat eli niissä on yhtä monta alkiota. Koska niissä on yhteensä 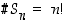 alkiota, joukossa
alkiota, joukossa 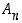 on tästä määrästä puolet, kuten väitettiin.
on tästä määrästä puolet, kuten väitettiin.

Esimerkki 4.3.7.
Ryhmän
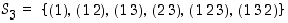
alkioista puolet ovat parillisia:
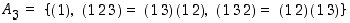 .
.

Opiskelutehtävä 42. (Alternoiva ryhmä)
Luettele alternoivan ryhmän 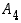 alkiot.
alkiot.
Vinkki tehtävään 42
Opiskelutehtävä 43. (Alternoivan ryhmän alkiotyypit)
Anna ryhmissä 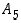 ,
,
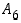 ja
ja 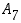 esimerkki kustakin erityyppisestä permutaation esityksestä erillisten kiertojen tulona. (Apu: Käytä lähtömallina ryhmää
esimerkki kustakin erityyppisestä permutaation esityksestä erillisten kiertojen tulona. (Apu: Käytä lähtömallina ryhmää 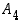 ,
missä kyseiset esimerkkityypit ovat
,
missä kyseiset esimerkkityypit ovat 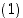 ,
,
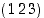 ja
ja 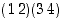 . Lukujen vaihtelua ei siis tarvitse huomioida.)
. Lukujen vaihtelua ei siis tarvitse huomioida.)
Vinkki tehtävään 43
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
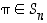 voidaan esittää vaihtojen tulona. Tällainen esitys ei ole kuitenkaan yksikäsitteinen, koska aina voidaan mihin tahansa esitykseen lisätä esimerkiksi tulopari
voidaan esittää vaihtojen tulona. Tällainen esitys ei ole kuitenkaan yksikäsitteinen, koska aina voidaan mihin tahansa esitykseen lisätä esimerkiksi tulopari 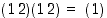 . Tällöin kuitenkin lisätään kaksi vaihtoa, ja yleisemmin osoittautuukin, että vaihtoja voidaan lisätä tai vähentää aina vain parillinen määrä. Perustellaan se seuraavaksi. Avuksi tarvitsemme ensin paria apulausetta.
. Tällöin kuitenkin lisätään kaksi vaihtoa, ja yleisemmin osoittautuukin, että vaihtoja voidaan lisätä tai vähentää aina vain parillinen määrä. Perustellaan se seuraavaksi. Avuksi tarvitsemme ensin paria apulausetta. 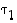 ja
ja 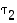 eri vaihtoja, joista
eri vaihtoja, joista 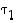 vaihtaa luvun
vaihtaa luvun 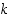 (ts.
(ts. 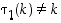 ). Silloin tulo
). Silloin tulo 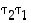 voidaan esittää kahden sellaisen vaihdon
voidaan esittää kahden sellaisen vaihdon 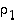 ja
ja 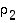 tulona,
tulona, 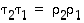 ,
joista vaihto
,
joista vaihto 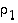 ei vaihda lukua
ei vaihda lukua 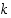 miksikään, mutta
miksikään, mutta 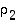 vaihtaa sen (ts.
vaihtaa sen (ts. 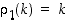 ,
mutta
,
mutta 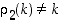 ).
). 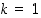 ja
ja 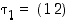 . Silloin on oleellisesti seuraavat kolme mahdollisuutta:
. Silloin on oleellisesti seuraavat kolme mahdollisuutta: 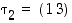 ,
niin
,
niin 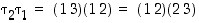 .
. 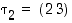 ,
niin
,
niin 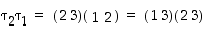 .
. 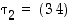 ,
niin
,
niin 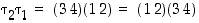 .
. 
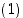 voidaan esittää tulona, jossa on
voidaan esittää tulona, jossa on 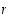 vaihtoa, ja jos
vaihtoa, ja jos 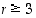 ,
voidaan
,
voidaan 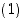 esittää tulona, jossa on vain
esittää tulona, jossa on vain 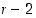 vaihtoa.
vaihtoa. 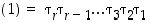 .
. 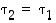 ,
on
,
on 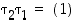 ja tämä tulo voidaan permutaation
ja tämä tulo voidaan permutaation 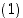 esityksestä poistaa, jolloin saadaan vaadittu lyhyempi esitys.
esityksestä poistaa, jolloin saadaan vaadittu lyhyempi esitys. 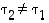 . Merkitään, että
. Merkitään, että 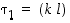 ,
missä
,
missä 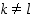 . Koska
. Koska 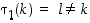 ,
on apulauseen
,
on apulauseen 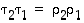 ,
missä
,
missä 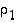 ja
ja 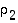 ovat sellaisia vaihtoja, että
ovat sellaisia vaihtoja, että 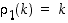 ja
ja 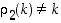 . Siten
. Siten 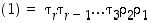 .
. 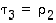 ,
voidaan tulo
,
voidaan tulo 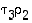 taas poistaa, jolloin saadaan vaadittu lyhyempi esitys.
taas poistaa, jolloin saadaan vaadittu lyhyempi esitys. 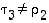 ,
löytyvät samoin kuin edellä vaihdot
,
löytyvät samoin kuin edellä vaihdot 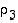 ja
ja 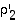 siten, että
siten, että 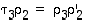 ,
,
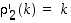 ja
ja 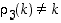 . Näin jatketaan.
. Näin jatketaan. 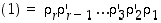 ,
,
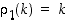 ,
,
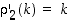 ,
,
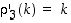 ,
…,
,
…, 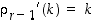 ,
mutta
,
mutta 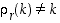 . Edelleen saataisiin, että
. Edelleen saataisiin, että 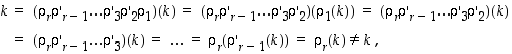

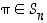 esityksessä vaihtojen tulona on joko aina parillinen tai aina pariton määrä vaihtoja.
esityksessä vaihtojen tulona on joko aina parillinen tai aina pariton määrä vaihtoja. 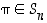 seuraavat esitykset vaihtojen tulona:
seuraavat esitykset vaihtojen tulona: 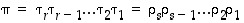 .
. 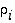 käänteisvaihdolla ja huomioimalla lopuksi, että se on sama vaihto
käänteisvaihdolla ja huomioimalla lopuksi, että se on sama vaihto 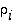 ,
saadaan seuraava päättelyketju:
,
saadaan seuraava päättelyketju: 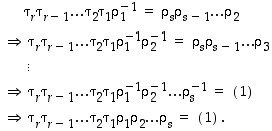
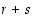 vaihdon tulona. Lauseen väitteen todistamiseksi riittää tämän jälkeen osoittaa, että
vaihdon tulona. Lauseen väitteen todistamiseksi riittää tämän jälkeen osoittaa, että 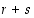 on parillinen.
on parillinen. 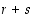 olisi pariton, voisi apulauseen
olisi pariton, voisi apulauseen 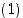 esitystä lyhentää ensin
esitystä lyhentää ensin 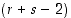 −pituiseksi, sitten
−pituiseksi, sitten 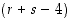 −pituiseksi, jne, kunnes saataisiin jokin 1−pituinen esitys
−pituiseksi, jne, kunnes saataisiin jokin 1−pituinen esitys 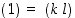 . Mutta tämä ei selvästikään ole mahdollista. Siten luku
. Mutta tämä ei selvästikään ole mahdollista. Siten luku 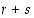 ja sen myötä myös
ja sen myötä myös 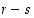 on parillinen eli joko molemmat luvuista
on parillinen eli joko molemmat luvuista 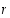 ja
ja 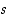 ovat parillisia tai sitten molemmat ovat parittomia. Lauseen väite on todistettu.
ovat parillisia tai sitten molemmat ovat parittomia. Lauseen väite on todistettu. 
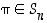 sanotaankin olevan
parillinen
sanotaankin olevan
parillinen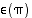 on
on 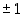 ; parilliselle
; parilliselle 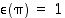 ja parittomalle
ja parittomalle 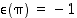 .
. 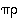 merkki saadaan tekijöiden
merkki saadaan tekijöiden 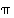 ja
ja 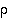 merkkien tulona eli
merkkien tulona eli 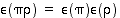 .
. 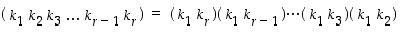 .
. 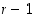 vaihtoa, joten näemme, että
vaihtoa, joten näemme, että 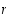 −kierto on parillinen, mikäli sen pituus
−kierto on parillinen, mikäli sen pituus  on pariton, ja pariton, mikäli
on pariton, ja pariton, mikäli 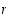 on parillinen. Toisin sanoen, kierron merkki saadaan kaavasta
on parillinen. Toisin sanoen, kierron merkki saadaan kaavasta 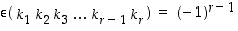 .
. 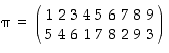
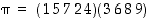 .
. 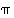 näiden tulona pariton. Sama päätelmä voidaan tehdä myös merkistä
näiden tulona pariton. Sama päätelmä voidaan tehdä myös merkistä 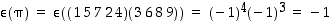 .
. 
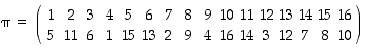
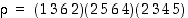 vaihtojen tulona. Ovatko ne parillisia vai parittomia?
vaihtojen tulona. Ovatko ne parillisia vai parittomia? 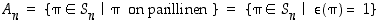 .
. 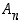 alkioille pätee:
alkioille pätee: 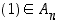 ,
,
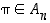 ,
niin myös
,
niin myös 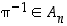 ,
,
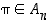 ja
ja 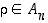 ,
niin myös
,
niin myös 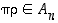 .
. 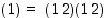 ,
on
,
on 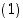 parillinen.
parillinen. 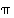 olisi käänteispermutaatio
olisi käänteispermutaatio 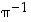 pariton, olisi niiden tulo
pariton, olisi niiden tulo 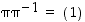 pariton vastoin edellisen kohdan tulosta.
pariton vastoin edellisen kohdan tulosta. 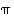 ja
ja 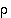 merkit ovat
merkit ovat 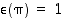 ja
ja 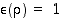 ,
joten
,
joten 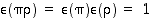 eli
eli 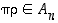 .
. 
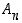 on ryhmän
on ryhmän 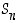 aliryhmä
aliryhmä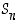 . Ryhmää
. Ryhmää 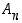 sanotaan
astetta
sanotaan
astetta 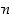 olevaksi
olevaksi 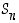 alkioista.
alkioista. 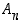 on
on 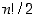 eri alkiota.
eri alkiota. 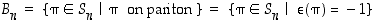 .
. 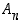 ja
ja 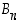 on
on 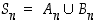 ja
ja 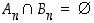 .
. 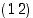 ,
saamme tulokseksi parittoman permutaation. Voimme siis määritellä kuvauksen
,
saamme tulokseksi parittoman permutaation. Voimme siis määritellä kuvauksen 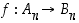 asettamalla
asettamalla 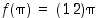 . Osoitamme, että tämä kuvaus on bijektio.
. Osoitamme, että tämä kuvaus on bijektio. 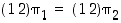 saadaan
saadaan 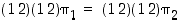 eli
eli 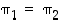 . Kuvaus
. Kuvaus 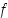 on siten injektio. Toisaalta jokaiselle parittomalle
on siten injektio. Toisaalta jokaiselle parittomalle 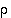 on permutaatio
on permutaatio 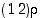 parillinen ja
parillinen ja 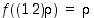 . Kuvaus
. Kuvaus 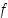 on siten myös surjektio.
on siten myös surjektio. 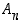 ja
ja 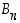 ovat siis yhtä mahtavat eli niissä on yhtä monta alkiota. Koska niissä on yhteensä
ovat siis yhtä mahtavat eli niissä on yhtä monta alkiota. Koska niissä on yhteensä 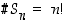 alkiota, joukossa
alkiota, joukossa 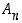 on tästä määrästä puolet, kuten väitettiin.
on tästä määrästä puolet, kuten väitettiin. 
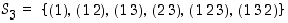
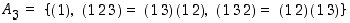 .
. 
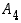 alkiot.
alkiot. 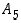 ,
,
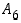 ja
ja 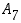 esimerkki kustakin erityyppisestä permutaation esityksestä erillisten kiertojen tulona. (Apu: Käytä lähtömallina ryhmää
esimerkki kustakin erityyppisestä permutaation esityksestä erillisten kiertojen tulona. (Apu: Käytä lähtömallina ryhmää 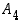 ,
missä kyseiset esimerkkityypit ovat
,
missä kyseiset esimerkkityypit ovat 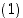 ,
,
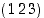 ja
ja 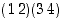 . Lukujen vaihtelua ei siis tarvitse huomioida.)
. Lukujen vaihtelua ei siis tarvitse huomioida.) 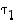 ,
,
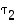 ,
…,
,
…, 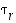 vaihtoja. Osoita, että
vaihtoja. Osoita, että 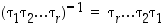 .
. 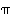 ja
ja 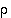 permutaatioilla
permutaatioilla 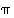 ja
ja 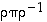 on aina sama merkki.
on aina sama merkki.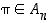 voidaan esittää 3−kiertojen tulona. (Vihje: Käytä hyväksi tietoa, että jokainen permutaatio voidaan esittää muotoa
voidaan esittää 3−kiertojen tulona. (Vihje: Käytä hyväksi tietoa, että jokainen permutaatio voidaan esittää muotoa 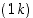 olevien vaihtojen tulona, ja yhdistele sitten näitä pareittain.)
olevien vaihtojen tulona, ja yhdistele sitten näitä pareittain.)