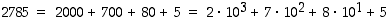 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Kun kirjoitamme esimerkiksi luvun 2785, tarkoitamme sillä lukua, joka saadaan, kun lasketaan yhteen kaksi tuhatta, seitsemän sataa, kahdeksan kymmentä ja viisi yksikköä. Toisin sanoen
Meistä on selvää, että jokainen positiivinen kokonaisluku 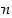 voidaan esittää ns.
desimaalimuodossa eli 10−kantaisessa muodossa
voidaan esittää ns.
desimaalimuodossa eli 10−kantaisessa muodossa
missä luvut 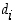 ovat kokonaislukuja ja
ovat kokonaislukuja ja 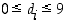 . Tällä tarkoitamme summaesitystä
. Tällä tarkoitamme summaesitystä
Desimaaliesityksen etunahan on se, että kymmenellä merkillä 0, 1, …, 9 pystytään ilmaisemaan isohkojakin lukuja.
Mihin tämä desimaaliesitys itse asiassa perustuu? Entä onko luvulla 10 jokin erityinen ominaisuus, joka mahdollistaa tällaiset esitykset? Voisiko luvut esittää vähemminkin merkein? Voisiko kaikki kokonaisluvut esittää käyttäen peräti vain kahta merkkiä, esimerkiksi nollaa ja ykköstä?
Katsotaan kertoimien muotoutumista ensin luvulle 2785. Muodostetaan jakoyhtälöt
Tämä menettely voidaan yleistää mielivaltaiselle positiiviselle kokonaisluvulle 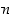 . Muodostetaan jakoyhtälön mukaisesti peräkkäiset yhtälöt
. Muodostetaan jakoyhtälön mukaisesti peräkkäiset yhtälöt
Tässä kaikki jakojäännökset  ,
,
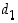 ,
,
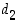 ,
… toteuttavat ehdon
,
… toteuttavat ehdon 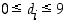 . Kertoimet
. Kertoimet 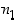 ,
,
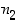 ,
,
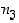 ,
… taas muodostavat laskevan kokonaislukujonon
,
… taas muodostavat laskevan kokonaislukujonon 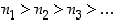 . Pienimmän alkion periaatteen mukaan näin ei voi kuitenkaan jatkua loputtomasti. Jollekin indeksille
. Pienimmän alkion periaatteen mukaan näin ei voi kuitenkaan jatkua loputtomasti. Jollekin indeksille 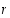 tulee siten vastaan yhtälö
tulee siten vastaan yhtälö 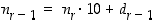 ,
jossa
,
jossa 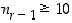 ja
ja 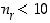 (paitsi jos
(paitsi jos 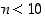 ,
jolloin on jo
,
jolloin on jo 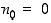 ). Silloin
). Silloin 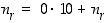 . Kun valitaan
. Kun valitaan 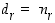 ja sijoitetaan luvun
ja sijoitetaan luvun 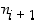 esitys yksi kerrallaan edellisen luvun
esitys yksi kerrallaan edellisen luvun 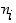 esitykseen, saadaan luvulle
esitykseen, saadaan luvulle 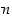 yllä mainittu esitys
yllä mainittu esitys
Käytetäänkö edellä olevassa menettelyssä jotain luvun 10 erityistä ominaisuutta? Ei, käytetään vain sitä, että tämän luvun suhteen voidaan muodostaa jakoyhtälö, jossa jakotulos on jaettavaa pienempi. Sama menettely voidaan tehdä siten minkä tahansa ykköstä isomman kokonaisluvun suhteen. Tuloksena tästä kaikesta on, että jos 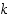 on ykköstä isompi kokonaisluku, on jokaisella positiivisella kokonaisluvulla
on ykköstä isompi kokonaisluku, on jokaisella positiivisella kokonaisluvulla 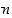 esitys
esitys
missä 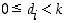 . Tämän sanotaan olevan luvun
. Tämän sanotaan olevan luvun 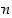 esitys
esitys 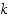 −
kantaisessa
lukujärjestelmässä. Lukua
−
kantaisessa
lukujärjestelmässä. Lukua 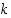 sanotaan lukujärjestelmän
kantaluvuksi. Desimaaliesityksen tapaan se voidaan merkitä lyhyemmin muodossa
sanotaan lukujärjestelmän
kantaluvuksi. Desimaaliesityksen tapaan se voidaan merkitä lyhyemmin muodossa
Tarkempi todistus esityksen olemassaolosta voidaan tehdä täydellisellä induktiolla. Samalla voi osoittaa, että tällainen esitys on yksikäsitteinen, ts. jos esityksessä yksikin numero vaihdetaan toiseksi, saadaan eri luku.
Negatiivisille kokonaisluvuille vastaava esitys saadaan sen itseisarvon esityksestä vaihtamalla kaikkien kertoimien 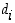 merkit negatiivisiksi. Lyhennetyssä merkinnässä miinusmerkki kirjoitetaan kuitenkin vain kerran koko esityksen eteen.
merkit negatiivisiksi. Lyhennetyssä merkinnässä miinusmerkki kirjoitetaan kuitenkin vain kerran koko esityksen eteen.
Tietokonemaailmassa käytetään erityisesti kantalukuja 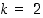 ,
,
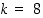 ja
ja 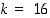 . Kokonaislukujen esityksiä näissä lukujärjestelmissä sanotaan vastaavasti
binääri-,
oktaali- ja
heksadesimaaliesityksiksi. Binääriesityksessä käytetään vain numeroita 0 ja 1, oktaaliesityksessä taas numeroita 0, 1, …, 7. Heksadesimaaliesityksessä käytetään yleisesti numeroiden 0, 1, 2, …, 9 jälkeen desimaalilukujen 10, 11, 12, 13, 14 ja 15 tilalla merkkejä A, B, C, D, E ja F.
. Kokonaislukujen esityksiä näissä lukujärjestelmissä sanotaan vastaavasti
binääri-,
oktaali- ja
heksadesimaaliesityksiksi. Binääriesityksessä käytetään vain numeroita 0 ja 1, oktaaliesityksessä taas numeroita 0, 1, …, 7. Heksadesimaaliesityksessä käytetään yleisesti numeroiden 0, 1, 2, …, 9 jälkeen desimaalilukujen 10, 11, 12, 13, 14 ja 15 tilalla merkkejä A, B, C, D, E ja F.
Miten sitten kokonaisluvun esitys toisessa lukujärjestelmässä voidaan löytää? Tarkastellaan ensin kymmenjärjestelmässä esitetyn luvun muuntamista 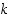 −kantaiseen järjestelmään. Periaatteessa on kaksi mahdollisuutta, 'ylhäältä alas' ja 'alhaalta ylös'. Jälkimmäisessä määrätään ensin 'vähäpainoisin' numero
−kantaiseen järjestelmään. Periaatteessa on kaksi mahdollisuutta, 'ylhäältä alas' ja 'alhaalta ylös'. Jälkimmäisessä määrätään ensin 'vähäpainoisin' numero 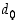 ja edetään sitten yksi kerrallaan 'suuripainoisimpaan' numeroon
ja edetään sitten yksi kerrallaan 'suuripainoisimpaan' numeroon 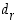 . Tämä menettely on itse asiassa aivan sama kuin yllä esitetty menetelmä, jolla esityksen olemassaolo perusteltiin. Jakoyhtälöistä
. Tämä menettely on itse asiassa aivan sama kuin yllä esitetty menetelmä, jolla esityksen olemassaolo perusteltiin. Jakoyhtälöistä
saadaan luettua esitys 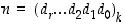 (kun
(kun 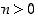 ).
).
Toinen tapa huomataan esityksestä
Tässä esityksessä suluissa oleva luku on pienempi kuin 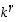 ,
joten se on itse asiassa se jakojäännös
,
joten se on itse asiassa se jakojäännös 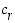 ,
joka saadaan, kun luku
,
joka saadaan, kun luku 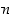 jaetaan luvulla
jaetaan luvulla 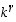 . Toisaalta ehtojen
. Toisaalta ehtojen 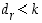 ja
ja 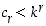 perusteella on
perusteella on
Tämän mukaan 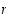 on suurin sellainen potenssi, että
on suurin sellainen potenssi, että 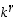 ei ylitä lukua
ei ylitä lukua 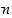 ja johtava numero
ja johtava numero 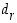 saadaan silloin jakoyhtälöstä
saadaan silloin jakoyhtälöstä 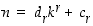 . Seuraava numero saadaan jakoyhtälöstä
. Seuraava numero saadaan jakoyhtälöstä 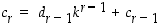 ,
jne. Tämä menettely on käyttökelpoinen varsinkin silloin, kun tiedetään valmiiksi kantaluvun
,
jne. Tämä menettely on käyttökelpoinen varsinkin silloin, kun tiedetään valmiiksi kantaluvun  potenssit.
potenssit.
Muunnetaan kymmenjärjestelmän luku 109 binäärijärjestelmään.
Ensimmäinen tapa. Kakkosella jakaen muodostetaan jakoyhtälöt
Jakojäännökset takaperoisesti lukien saadaan esitys 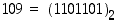 .
.
Toinen tapa. Kakkosen potensseista
huomataan, että 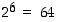 on suurin potenssi, joka ei ylitä lukua 109. Aloitetaan jakaminen sillä ja edetään sitten jakamalla saadut jakojäännökset aina edellisellä kakkosen potenssilla:
on suurin potenssi, joka ei ylitä lukua 109. Aloitetaan jakaminen sillä ja edetään sitten jakamalla saadut jakojäännökset aina edellisellä kakkosen potenssilla:
Kakkosen potenssien kertoimista saadaan nyt esitys 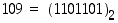 .
.
Muunnetaan kymmenjärjestelmän luku 2000 heksadesimaalijärjestelmään. Huomaten, että 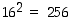 ,
muodostetaan jakoyhtälöt
,
muodostetaan jakoyhtälöt
Tehtävä. Muunna heksadesimaaliluvut 1, 2, …, F binääri- ja oktaaliluvuiksi.
Muista lukujärjestelmistä kymmenjärjestelmään päin siirtyminen on suoraviivaisempaa. Esityksestä 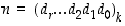 saadaan nimittäin kymmenjärjestelmän esitys
saadaan nimittäin kymmenjärjestelmän esitys
kunhan vain ensin lasketaan tarvittavat kantaluvun potenssit.
Muunnetaan heksadesimaaliluku 1B2F kymmenjärjestelmään. Se tarkoittaa lukua
Binääriluku 11111010000 vuorostaan tarkoittaa kymmenjärjestelmän lukua
Opiskelutehtävä 18. (Heksadesimaaliluvun muunto)
Muunna heksadesimaaliluku ABC ensin desimaaliluvuksi ja sitten binääriluvuksi.
1. Ilmoita luku 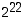 heksadesimaalilukuna.
heksadesimaalilukuna.
2. Muunna heksadesimaaliluku 12AB binääriluvuksi.
3. Olkoon 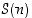 kokonaisluvun
kokonaisluvun 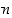 numeroiden summa sen desimaaliesityksessä.
numeroiden summa sen desimaaliesityksessä.
(a) Onko olemassa lukua 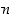 ,
jolle
,
jolle 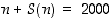 ?
?