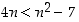 ,
kun
,
kun 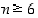 . Todistus matemaattisella induktiolla.
. Todistus matemaattisella induktiolla.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Olkoon
P(
n) väite, että luonnollisella luvulla
n pätee 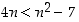 ,
kun
,
kun 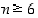 . Todistus matemaattisella induktiolla.
. Todistus matemaattisella induktiolla.
1° Kun
n = 6, on 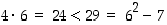 ,
joten
P(6) pätee.
,
joten
P(6) pätee.
2° Induktio-oletus:
P(
n) pätee eli 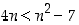 .
.
3° Induktioväite:
P(
n + 1) pätee eli 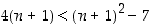 .
.
4° Induktiotodistus: tämä epäyhtälötodistus, kuten epäyhtälötodistukset hyvin usein, voidaan tehdä lähtemällä liikkeelle väitetyn epäyhtälön jommasta kummasta puolesta ja pyrkimällä arvioimaan epäyhtälöä sopivasti ylös- tai alaspäin, siitä riippuen kummasta puolesta aloitettiin.
Ratkaisutapa
1. Aloittamalla induktioväitteen epäyhtälön vasemmasta puolesta saadaan, että 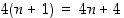 . Halutaan osoittaa, että
. Halutaan osoittaa, että 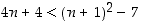 . Koska tämän epäyhtälön oikea puoli voidaan kirjoittaa muodossa
. Koska tämän epäyhtälön oikea puoli voidaan kirjoittaa muodossa 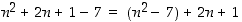 ja koska induktio-oletuksen mukaan
ja koska induktio-oletuksen mukaan 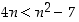 ,
riittää osoittaa, että
,
riittää osoittaa, että 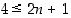 . Kun
. Kun 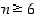 ,
pitää tämä väite paikkaansa, sillä tällöin
,
pitää tämä väite paikkaansa, sillä tällöin 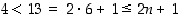 .
.
Ratkaisutapa
2. Aloitetaan nyt induktioväitteen epäyhtälön oikeasta puolesta, jolloin saadaan, että 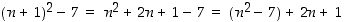 . Täytyy osoittaa, että
. Täytyy osoittaa, että 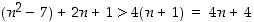 . Koska induktio-oletuksen mukaan
. Koska induktio-oletuksen mukaan 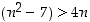 ,
riittää osoittaa, että
,
riittää osoittaa, että 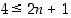 . Kun
. Kun 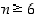 ,
pitää tämä väite selvästi paikkaansa, sillä
,
pitää tämä väite selvästi paikkaansa, sillä 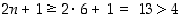 ja näin väite on todistettu.
ja näin väite on todistettu.
Lisätietoja. Tehtävä voitaisiin ratkaista myös muuten kuin matemaattisella induktiolla − käyttäen esimerkiksi koulusta ehkä induktiota tutumpaa lähestymistapaa. Tarkastellaan alkuperäisen väitteen epäyhtälöä reaalilukualueella, ja käytetään siksi muuttujan
n sijasta muuttujaa
x. Olkoon
Q(
x) väite, jonka mukaan 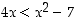 . Tämä väite voidaan kirjoittaa myös muodossa
. Tämä väite voidaan kirjoittaa myös muodossa 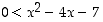 .
.
Havaitaan, että saadun epäyhtälön oikea puoli on toisen asteen polynomi, jonka kuvaaja on ylöspäin aukeava paraabeli (paraabeli on ylöspäin aukeava, sillä polynomin toisen asteen termin 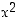 kerroin on positiivinen). Kuvaaja on siis seuraavantyyppinen
kerroin on positiivinen). Kuvaaja on siis seuraavantyyppinen
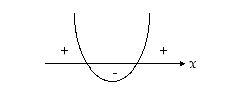
Polynomi on arvoltaan nolla niillä muuttujan arvoilla, joilla sen kuvaaja leikkaa x-askelin ja negatiivinen nollakohtiensa välisillä muuttujan arvoilla.
Huomautus. Toisen asteen polynomilla voi olla nolla, yksi tai kaksi nollakohtaa. Kukin paraabeli voi olla joko ylös- tai alaspäin aukeava riippuen termin 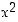 kertoimen merkistä.
kertoimen merkistä.
Toisen asteen yhtälön 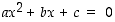 ratkaisukaava on: (
ratkaisukaava on: (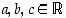 ,
,
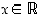 ,
,
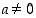 )
)
Etsitään nyt nollakohdat toisen asteen yhtälön ratkaisukaavan avulla eli etsitään yhtälön 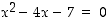 ratkaisut:
ratkaisut:
Edellistä polynomin kuvaajaa hyödyntämällä nollakohdat näkyvät kuvassa seuraavasti:
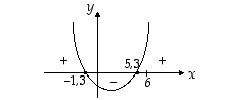
Koska tehtävän ehtojen mukaan alkuperäinen muuttuja
n on positiivinen, voidaan ratkaisualue 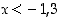 jättää huomiotta. Siten jää jäljelle alue
jättää huomiotta. Siten jää jäljelle alue 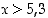 . Koska tehtävää oltiin ratkaisemassa vain kokonaisluvuille, havaitaan, että väite pätee kaikilla
. Koska tehtävää oltiin ratkaisemassa vain kokonaisluvuille, havaitaan, että väite pätee kaikilla 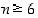 .
.
Lisätietoja. Halutessaan tarkastelua voisi vielä tarkentaa osoittamalla, että paraabelin derivaatta on positiivinen kun 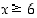 ja siis myös kun
ja siis myös kun 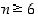 ,
jolloin paraabeli on aina aidosti kasvava eikä siten voi enää saada negatiivisia arvoja millään
,
jolloin paraabeli on aina aidosti kasvava eikä siten voi enää saada negatiivisia arvoja millään 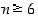 .
.
Koska väite
Q(
x) pätee kaikilla 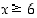 ,
pätee väite
P(
n) kaikilla
,
pätee väite
P(
n) kaikilla 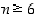 ,
sillä
,
sillä  .
.
Huomautus. Mikäli toisen asteen yhtälön ratkaisukaavassa neliöjuuren alle jäävä lauseke ( diskriminantti) on negatiivinen, ei kyseisellä toisen asteen yhtälöllä ole reaalilukuratkaisua, jos diskriminantti on nolla, on yhtälöllä tasan yksi reaalilukuratkaisu ja jos diskriminantti on positiivinen, on reaalilukuratkaisuja kaksi.
[Opiskelutehtävä 11] [Vinkki tehtävään 11]