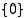 ; sanotaan myös, että jokaisen sellaisen joukon alkioiden lukumäärä eli
mahtavuus on 1. Vastaavasti joukon
; sanotaan myös, että jokaisen sellaisen joukon alkioiden lukumäärä eli
mahtavuus on 1. Vastaavasti joukon 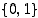 mahtavuus on 2. Ja niin edelleen. Näin saadaan kokoon
luonnollisten lukujen joukko
mahtavuus on 2. Ja niin edelleen. Näin saadaan kokoon
luonnollisten lukujen joukko
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Joukot voidaan luokitella niiden sisältämien alkioiden lukumäärän avulla. Tyhjässä joukossa ei ole alkioita ollenkaan. Sen alkioiden lukumäärää merkitään symbolilla 0, ts. siinä on 0 alkiota. Luvulla 1 merkitään niiden joukkojen luokkaa, jossa on yhtä monta alkiota kuin esimerkiksi joukossa 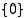 ; sanotaan myös, että jokaisen sellaisen joukon alkioiden lukumäärä eli
mahtavuus on 1. Vastaavasti joukon
; sanotaan myös, että jokaisen sellaisen joukon alkioiden lukumäärä eli
mahtavuus on 1. Vastaavasti joukon 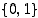 mahtavuus on 2. Ja niin edelleen. Näin saadaan kokoon
luonnollisten lukujen joukko
mahtavuus on 2. Ja niin edelleen. Näin saadaan kokoon
luonnollisten lukujen joukko
Luonnollisia lukuja voidaan varsin 'luonnollisesti' laskea yhteen ja kertoa keskenään. Esimerkiksi 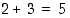 tarkoittaa, että jos 2−alkioisen joukon alkioihin lisätään jonkin 3−alkioisen joukon alkiot, saadaan aina 5−alkioinen joukko. Vastaavasti
tarkoittaa, että jos 2−alkioisen joukon alkioihin lisätään jonkin 3−alkioisen joukon alkiot, saadaan aina 5−alkioinen joukko. Vastaavasti 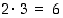 tarkoittaa, että sellaisista alkiopareista, joissa ensimmäinen valitaan 2−alkioisesta joukosta ja toinen 3−alkioisesta joukosta, saadaan koottua 6−alkioinen joukko.
tarkoittaa, että sellaisista alkiopareista, joissa ensimmäinen valitaan 2−alkioisesta joukosta ja toinen 3−alkioisesta joukosta, saadaan koottua 6−alkioinen joukko.
Järjestyskin saadaan luonnollisesti. Esimerkiksi 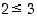 ,
koska jokaisella 2−alkioisen joukon alkiolla on aina oma vastineensa missä tahansa 3−alkioisessa joukossa. Emme kuitenkaan perehdy tässä yhteen- ja kertolaskun tai järjestyksen problematiikkaan sen tarkemmin, vaan oletamme peruslaskutoimitukset tunnetuiksi.
,
koska jokaisella 2−alkioisen joukon alkiolla on aina oma vastineensa missä tahansa 3−alkioisessa joukossa. Emme kuitenkaan perehdy tässä yhteen- ja kertolaskun tai järjestyksen problematiikkaan sen tarkemmin, vaan oletamme peruslaskutoimitukset tunnetuiksi.
Edellä mainittujen ominaisuuksien lisäksi luonnollisilla luvuilla on eräs hyvin tärkeä ja luonnollisen tuntuinen ominaisuus, joka voidaan ottaa (tai joudutaan ottamaaan) aksioomaksi. Tarkastellaan sitä varten ensin seuraavien yhtälöiden kuvaamaa päättelytehtävää:
Miten päätellä lukuun 99 päättyvä summa? Tai yleisemmin parittomien lukujen summa annettuun (mahdollisesti hyvinkin suureen) lukuun asti? Tähän olisi helppo vastata, jos viimeisimmän yhtälön oikealle puolelle keksittäisiin jokin selkeä lauseke. Ensimmäisistä yhtälöistä näkyy, että jokin neliölauseke olisi hyvä ehdokas, olisikohan yksinkertaisesti 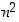 . Mutta miten voimme tietää, onko se oikein?
. Mutta miten voimme tietää, onko se oikein?
Kaikkia summia emme voi kuvitella pystyvämme erikseen tarkistamaan. Tämän pulman ratkaisemme ajattelemalla rekursiivisesti: Toteamme ensin, että ensimmäinen yhtälö pitää paikkansa. Sitten huomaamme, että edellinen summa esiintyy aina seuraavan osana: toisen yhtälön summassa esiintyy ensimmäisen yhtälön summa (tosin typistyneenä pelkäksi luvuksi 1 ), kolmannen yhtälön summassa esiintyy osana toisen yhtälön summa 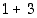 ,
neljännen yhtälön summassa esiintyy osana kolmannen yhtälön summa
,
neljännen yhtälön summassa esiintyy osana kolmannen yhtälön summa 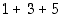 ,
jne.
,
jne.
Saamme siis seuraavan summatuloksen varsin helposti, jos tiedämme edellisen tuloksen. Jospa vielä pystyisimme löytämään yleispätevän säännön siitä, miksi ja miten edellisen rivin tulos antaa aina seuraavan rivin tuloksen!
Tarkastellaan lähemmin kahta peräkkäistä summaa
Oletetaan, että edelliselle summalle pätee yhtälö
Tarkastellaan sitten jälkimmäistä summaa
Sen alkuosassa esiintyy edellinen summa, jonka siis otaksumme olevan 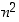 . Sijoittamalla sen saamme, että
. Sijoittamalla sen saamme, että
Olemme siten saaneet seuraavan säännön: aina jos edellisen summan tulos on 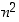 ,
on seuraavan summan tulos
,
on seuraavan summan tulos 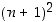 .
.
Tätä sääntöä käyttäen päättelemme seuraavasti: koska ensimmäinen summa antaa luvun 1 neliön, niin toinen summa antaa luvun 2 neliön, kolmas summa antaa luvun 3 neliön, neljäs summa antaa luvun 4 neliön, jne. Mutta mistä tiedämme, että sääntö pätee loputtomiin?
Tällaisen päättelyn matemaattiseksi oikeutukseksi tarvitsemme seuraavaa luonnollisten lukujen perusominaisuutta.
Aksiooma 2.1.1. (Induktioaksiooma)
Jos luonnollisten lukujen 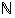 osajoukolle
osajoukolle 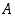 pätevät ehdot
pätevät ehdot
sisältää joukko 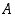 kaikki luonnolliset luvut eli
kaikki luonnolliset luvut eli 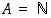 .
.
Nyt voimme muotoilla tuloksen, jota voidaan käyttää pykälän alussa esitetyn kaltaisten tehtävien tulosten todistamiseen.
Lause 2.1.2. (Täydellinen induktio eli matemaattinen induktio)
Olkoon 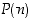 jokin luonnollisesta luvusta
jokin luonnollisesta luvusta 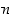 riippuva lause, jolle
riippuva lause, jolle
(b) jokaiselle 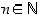 siitä, että
siitä, että 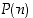 pätee, seuraa että
pätee, seuraa että 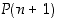 pätee.
pätee.
Todistus. Tarkastellaan joukkoa
Tälle joukolle pätee oletuksen mukaan ensinnäkin se, että 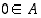 ,
ja toiseksi se, että jokaiselle
,
ja toiseksi se, että jokaiselle 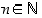 ehdosta
ehdosta 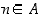 seuraa, että
seuraa, että 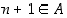 . Siten induktioaksiooman mukaan
. Siten induktioaksiooman mukaan 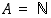 ,
ts. lause
,
ts. lause 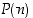 on aina tosi.
on aina tosi.
Täydellisessä induktiossa se väite, että 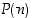 pätee, on
induktio-oletus,
ja se väite, että
pätee, on
induktio-oletus,
ja se väite, että 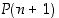 pätee, on
induktioväite. Oleellisin − ja yleensä vaikein − kohta induktiotodistuksessa on osoittaa oletuksen
pätee, on
induktioväite. Oleellisin − ja yleensä vaikein − kohta induktiotodistuksessa on osoittaa oletuksen 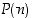 avulla väite
avulla väite 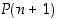 oikeaksi. Tätä sanotaan
induktioaskeleeksi. Sellaista päättelyä, jonka todistus perustuu täydelliseen induktioon, sanotaan myös
induktiopäättelyksi.
oikeaksi. Tätä sanotaan
induktioaskeleeksi. Sellaista päättelyä, jonka todistus perustuu täydelliseen induktioon, sanotaan myös
induktiopäättelyksi.
Täydellistä induktiota ei tarvitse aina aloittaa luvusta 0, vaan se voidaan aloittaa tarvittaessa jostain suuremmastakin luvusta. Näin saadaan seuraava induktiotodistuksen muoto.
Seuraus 2.1.3. ( Täydellinen induktio jostain luvusta alkaen)
Olkoon 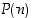 jokin luonnollisesta luvusta
jokin luonnollisesta luvusta 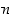 riippuva lause ja
riippuva lause ja 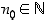 . Oletetaan, että
. Oletetaan, että
(b) jokaiselle 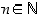 ,
jolle
,
jolle 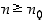 ,
siitä, että
,
siitä, että 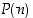 pätee, seuraa että
pätee, seuraa että 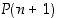 pätee.
pätee.
Tällöin 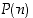 pätee kaikilla
pätee kaikilla 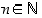 ,
joilla
,
joilla 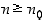 .
.
Kun tarkastellaan avointa lausetta 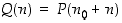 ,
huomataan, että sille pätevät täydellisen induktion oletukset. Siten
,
huomataan, että sille pätevät täydellisen induktion oletukset. Siten 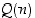 pätee aina eli
pätee aina eli 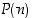 pätee kaikilla niillä
pätee kaikilla niillä 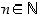 ,
joilla
,
joilla 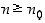 .
.
Palataan pykälän alussa esitettyyn tehtävään, jossa pyrittiin laskemaan parittomien lukujen summaa. Arvasimme silloin, että vastaukseksi tulisi
Osoitamme sen nyt oikeaksi täydellisellä induktiolla. Olkoon 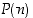 väite, että yllä oleva kaava pätee luvulle
väite, että yllä oleva kaava pätee luvulle 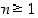 . Koska
. Koska 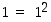 ,
väite
,
väite 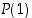 pätee. Oletetaan sitten induktio-oletuksena, että
pätee. Oletetaan sitten induktio-oletuksena, että 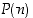 pätee, ts.
pätee, ts.
Pitää seuraavaksi osoittaa oikeaksi induktioväite eli että 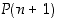 pätee. Toisin sanoen pitää osoittaa, että
pätee. Toisin sanoen pitää osoittaa, että
Lähdemme kehittämään yhtälön vasenta puolta tavoitteena saada se muunnettua oikean puolen lausekkeeksi:
Nyt huomaamme, että alkuosassa esiintyy väitteen 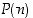 summa, jonka siis tiedämme induktio-oletuksen mukaan olevan
summa, jonka siis tiedämme induktio-oletuksen mukaan olevan 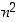 . Sijoittamalla sen saamme, että
. Sijoittamalla sen saamme, että
Olemme siten todistaneet induktioväitteen 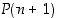 oikeaksi. Täydellisen induktion periaatteen mukaan siis väite
oikeaksi. Täydellisen induktion periaatteen mukaan siis väite 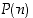 pätee kaikilla
pätee kaikilla 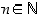 ,
joille
,
joille 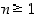 .
.
Osoitetaan täydellisellä induktiolla oikeaksi kaava
Olkoon sitä varten 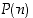 väite, että yllä oleva (ns. Gaussin) kaava pätee. Väite
väite, että yllä oleva (ns. Gaussin) kaava pätee. Väite 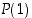 pitää paikkansa, koska
pitää paikkansa, koska 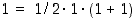 . Kun oletamme sitten, että väite
. Kun oletamme sitten, että väite 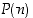 pätee, saamme sen avulla muokattua väitteen
pätee, saamme sen avulla muokattua väitteen 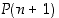 vasemman puolen summaa seuraavasti:
vasemman puolen summaa seuraavasti:
mikä osoittaakin jo, että 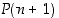 pätee. Induktiotodistus on käyty läpi, ja siten annettu kaava pätee kaikilla
pätee. Induktiotodistus on käyty läpi, ja siten annettu kaava pätee kaikilla 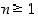 .
.
Olkoon 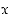 mielivaltainen reaaliluku. Osoitetaan, että
mielivaltainen reaaliluku. Osoitetaan, että
kaikilla luonnollisilla luvuilla 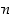 . Olkoon sitä varten
. Olkoon sitä varten 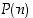 väite, että yllä oleva kaava pätee. Väite
väite, että yllä oleva kaava pätee. Väite 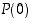 pätee, koska
pätee, koska 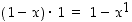 (yhtälön vasemmalla puolella käytetään hyväksi sopimusta
(yhtälön vasemmalla puolella käytetään hyväksi sopimusta 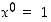 ). Kun sitten oletamme, että
). Kun sitten oletamme, että 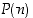 pätee, silloin
pätee, silloin
mikä osoittaa, että myös 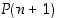 pätee. Induktiotodistus on siis käyty läpi, ja siten annettu kaava pätee kaikilla luonnollisilla luvuilla
pätee. Induktiotodistus on siis käyty läpi, ja siten annettu kaava pätee kaikilla luonnollisilla luvuilla 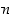 .
.
Opiskelutehtävä 10. (Potenssien summa induktiolla)
Tarkastele summia 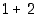 ,
,
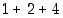 ,
,
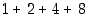 jne. Päättele yleinen sääntö, joka ilmoittaa, mikä tällaisen summan tulokseksi tulee. Osoita se oikeaksi. Mikä on siten summan
jne. Päättele yleinen sääntö, joka ilmoittaa, mikä tällaisen summan tulokseksi tulee. Osoita se oikeaksi. Mikä on siten summan 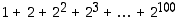 tulos?
tulos?
Opiskelutehtävä 11. (Epäsuuruus induktiolla 1)
Opiskelutehtävä 12. (Epäsuuruus induktiolla 2)
Induktioaksiooman avulla voimme todistaa seuraavan, ennalta ilmeisen tuntuisen tuloksen, jota tarvitsemme seuraavassa pykälässä ja myöhemminkin. Tämä ns. pienimmän alkion periaate on siinä mielessä tasavertainen induktioaksiooman kanssa, että se voidaan ottaa yhtä hyvin aksioomaksi ja induktioperiaate voidaan silloin todistaa sen avulla.
Lause 2.1.7. (Pienimmän alkion periaate)
Jokaisessa luonnollisten lukujen epätyhjässä osajoukossa on pienin alkio.
Todistus. Olkoon 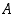 jokin luonnollisten lukujen epätyhjä osajoukko. Tarkastellaan apujoukkoa
jokin luonnollisten lukujen epätyhjä osajoukko. Tarkastellaan apujoukkoa
Tämä joukko ei ole tyhjä, sillä luku 0 täyttää ilman muuta sen määrittelyehdon.
Apuväite 1: Joukossa 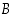 on alkio
on alkio 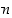 siten, että
siten, että 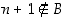 .
.
Tehdään vastaväite: Joukossa 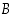 ei ole tällaista alkiota, jolloin jokaiselle
ei ole tällaista alkiota, jolloin jokaiselle 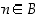 pätee, että
pätee, että 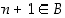 . Silloin joukko
. Silloin joukko 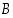 toteuttaa induktioaksiooman oletukset, joten sen mukaan
toteuttaa induktioaksiooman oletukset, joten sen mukaan 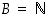 . Joukon
. Joukon 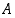 mielivaltaiselle alkiolle
mielivaltaiselle alkiolle 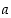 on
on 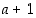 luonnollisena lukuna myös joukon
luonnollisena lukuna myös joukon 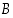 alkio. Siten joukon
alkio. Siten joukon 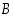 määritelmän mukaan olisi
määritelmän mukaan olisi 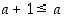 ,
mikä on selvä ristiriita. Vastaväite on siis väärin ja itse väite eli apuväite 1 oikein.
,
mikä on selvä ristiriita. Vastaväite on siis väärin ja itse väite eli apuväite 1 oikein.
Apuväite 2: Luku 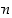 on joukon
on joukon 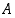 pienin alkio, ts.
pienin alkio, ts. 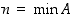 .
.
Koska 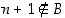 ,
on olemassa alkio
,
on olemassa alkio 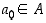 siten, että
siten, että 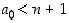 . Toisaalta
. Toisaalta 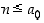 ,
joten on oltava
,
joten on oltava 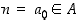 . Koska edelleen ehdon
. Koska edelleen ehdon 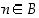 mukaan
mukaan 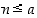 kaikilla
kaikilla 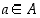 ,
on luku
,
on luku 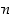 joukon
joukon 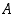 pienin alkio. Apuväite 2 ja siten koko lause on todistettu.
pienin alkio. Apuväite 2 ja siten koko lause on todistettu.
Pienimmän alkion periaatteesta seuraa ns. rajallisen laskeutumisen periaate: Jos lähdetään jostain positiivisesta kokonaisluvusta ja sitä pienennetään askel askeleelta yhä pienemmäksi luonnolliseksi luvuksi, ei tätä voida tehdä loputtomasti positiivisten lukujen joukossa, vaan jossain vaiheessa päädytään välttämättä nollaan.
4. Piirretään ympyrään  eri jännettä (
eri jännettä (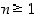 ). Osoita, että näiden rajoittamat ympyräalueet voidaan värittää kahdella värillä niin, että milloinkaan jänteen tai sen osankaan eri puolin ei tule saman väristä aluetta (samanväristen alueitten kärjet voivat koskettaa toisiaan).
). Osoita, että näiden rajoittamat ympyräalueet voidaan värittää kahdella värillä niin, että milloinkaan jänteen tai sen osankaan eri puolin ei tule saman väristä aluetta (samanväristen alueitten kärjet voivat koskettaa toisiaan).
5. Tason monikulmio on konveksi, jos kahta eri kärkeä yhdistävät janat ovat aina kokonaan kulmion sisällä (eli mikään sisäkulma ei ole oikokulmaa isompi).

Osoita, että kun 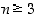 ,
on konveksissa
n−kulmiossa sisäkulmien summa
,
on konveksissa
n−kulmiossa sisäkulmien summa 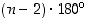 .
.
6. Oletetaan, että käytössäsi on kolmenkymmenen ja viidenkymmenen sentin postimerkkejä. Osoita, että näillä voit maksaa minkä tahansa vähintään kahdeksankymmentä senttiä maksavan tasakymmensenttisen postimaksun.
(Yllä määrittelyssä esiintyvä 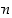 −
kertoma
−
kertoma 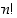 tarkoittaa tuloa
tarkoittaa tuloa 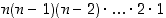 . Lisäksi sovitaan, että
. Lisäksi sovitaan, että 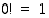 .)
.)
8. Todista induktiolla ns. Pascalin binomikaava:
missä 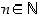 ja
ja 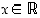 . (Vihje: Käytä edellisen tehtävän sääntöä hyväksi.)
. (Vihje: Käytä edellisen tehtävän sääntöä hyväksi.)
9. Osoita, että kaikilla reaaliluvuilla 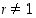 ja kaikilla luonnollisilla luvuilla
ja kaikilla luonnollisilla luvuilla 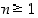 pätee ns.
geometrisen
sarjan
osasummakaava
pätee ns.
geometrisen
sarjan
osasummakaava