[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
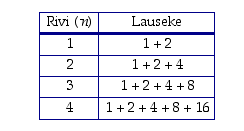
Taulukoidaan summalausekkeita ja yritetään tämän avulla havaita säännönmukaisuuksia.

Näyttäisi siltä, että lausekkeissa lasketaan yhteen kakkosen potensseja. Täydennetään taulukkoa näiden havaintojen perusteella. (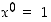 kaikilla nollasta poikkeavilla reaaliluvuilla
x. Myös
kaikilla nollasta poikkeavilla reaaliluvuilla
x. Myös 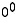 määritellään yleensä ykköseksi.)
määritellään yleensä ykköseksi.)

Ensimmäisellä rivillä viimeinen summattava kakkosen potenssi on 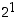 ,
toisella rivillä
,
toisella rivillä 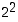 ,
kolmannella
,
kolmannella 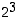 ja niin edelleen. Siten rivillä
n viimeinen kakkosen potenssi on varmaankin
ja niin edelleen. Siten rivillä
n viimeinen kakkosen potenssi on varmaankin 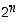 .
.
Lasketaan seuraavaksi summalausekkeiden arvot ja pyritään havainnoimaan tilanteesta jotain uutta.

Näyttäisi siltä, että kunkin summalausekkeen arvo on aina yhden pienempi kuin seuraavan rivin summalausekkeen viimeinen luku. Kirjoitetaan nyt lausekkeiden arvot tämän oletuksen avulla:

Ilmeisesti rivillä
n summalausekkeen arvo on 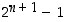 ja taulukon
n:s rivi olisi näin ollen:
ja taulukon
n:s rivi olisi näin ollen:
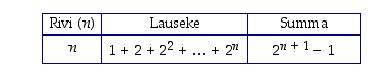
Todistetaan nyt matemaattisella induktiolla edellä muotoiltu oletus
n:nnen rivin summalausekkeen muodosta. Olkoon
P(
n) luonnollista lukua
n koskeva väite, jonka mukaan 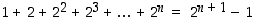 .
.
1° Kun 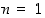 ,
niin
,
niin 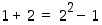 ,
joten
P(1) pätee.
,
joten
P(1) pätee.
2° Induktio-oletus:
P(
n) pätee, eli 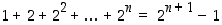 .
.
3° Induktioväite: P( n + 1) pätee, ts.
4° Induktiotodistus: kirjoitetaan induktioväitteen vasen puoli auki ja muokataan sitä. Tarkoituksena on saada yhtälön vasemman puolen lauseke kirjoitettua induktioväitteen yhtälön oikea puolen muotoon induktio-oletusta hyödyntämällä.
Väite P( n) pätee siis kaikilla positiivisilla kokonaisluvuilla n, joten konkreettisesti
Antti Käenmäki: Johdatus matematiikkaan, luentomuistiinpanot 2005: http://www.math.jyu.fi/~antakae/opetus/materiaali/johdatus.pdf
Tuomas Airaksinen: Johdatus matematiikkaan, luentomuistiinpanot: http://people.jyu.fi/~tuma/home/files/docs/johdmat.pdf
[Opiskelutehtävä 10] [Vinkki tehtävään 10]