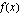 jatkuva. Lasketaan käyrien
jatkuva. Lasketaan käyrien 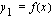 ja
ja 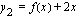 sekä suorien
sekä suorien 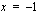 ja
ja 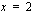 väliin jäävän alueen ala.
väliin jäävän alueen ala.
a ) Olkoon funktio 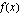 jatkuva. Lasketaan käyrien
jatkuva. Lasketaan käyrien 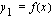 ja
ja 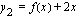 sekä suorien
sekä suorien 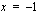 ja
ja 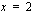 väliin jäävän alueen ala.
väliin jäävän alueen ala.
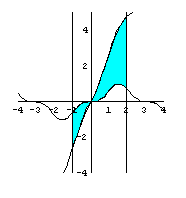
Ratkaistaan käyrien käyttäytyminen eli millä väleillä 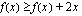 toteutuu.
toteutuu.
Välillä 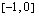 on voimassa
on voimassa 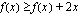 ja välillä
ja välillä 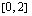 on voimassa
on voimassa 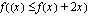 , joten käyrien
, joten käyrien 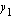 ja
ja 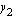 sekä suorien
sekä suorien 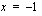 ja
ja 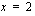 väliin jäävän alueen ala saadaan integroimalla seuraavasti.
väliin jäävän alueen ala saadaan integroimalla seuraavasti.
Käyrien 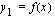 ja
ja 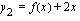 sekä suorien
sekä suorien 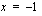 ja
ja 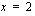 väliin jäävän alueen ala on
väliin jäävän alueen ala on 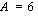 .
.
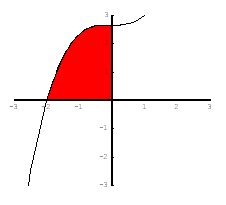
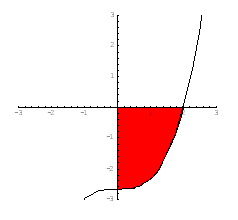
b ) Määritetään funktion 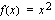 se integraalifunktio, jonka kuvaajan yhdessä koordinaattiakselien rajoittaman alueen ala on 4.
se integraalifunktio, jonka kuvaajan yhdessä koordinaattiakselien rajoittaman alueen ala on 4.
Lasketaan funktion 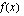 integraalifunktio
integraalifunktio 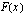 :
:
Integraalifunktio on kolmannen asteen polynomifunktio. Määrätään integroimisvakio 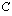 siten, että funktion kuvaajan ja koordinaattiakselien määräämän alueen pinta-ala on
siten, että funktion kuvaajan ja koordinaattiakselien määräämän alueen pinta-ala on 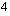 . Lasketaan sitä varten integraalifunktion
. Lasketaan sitä varten integraalifunktion 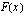 nollakohdat eli ratkaistaan yhtälö
nollakohdat eli ratkaistaan yhtälö 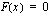 :
:
Vakio 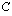 saadaan määrättyä, kun tiedetään alueen ala, joka saadaan integroimalla funktiota
saadaan määrättyä, kun tiedetään alueen ala, joka saadaan integroimalla funktiota 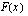 nollakohdasta
nollakohdasta 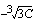 kohtaan
kohtaan 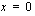 :
:
Ratkaistaan saadusta yhtälöstä vakion 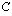 arvo. Poistetaan vakion kerroin ja korotetaan yhtälö puolittain potenssiin
arvo. Poistetaan vakion kerroin ja korotetaan yhtälö puolittain potenssiin 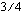 , jolloin mahdollinen negatiivinen ratkaisu täytyy ottaa huomioon (Juuri
, jolloin mahdollinen negatiivinen ratkaisu täytyy ottaa huomioon (Juuri 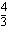 on positiivinen. Vertaa yhtälön
on positiivinen. Vertaa yhtälön 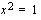 ratkaisu.).
ratkaisu.).
Saadaan integroimisvakiolle 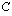 kaksi ratkaisua. Funktioita, joille tehtävässä annettu ehto on voimassa on siis kaksi.
kaksi ratkaisua. Funktioita, joille tehtävässä annettu ehto on voimassa on siis kaksi.
[Tehtävä 11.9][Vinkki tehtävään 11.9]