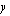 -akseli puolittaa suoran
-akseli puolittaa suoran 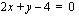 ja käyrän
ja käyrän 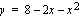 rajoittaman alueen pinta-alan.
rajoittaman alueen pinta-alan.
a ) Osoitetaan, että 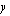 -akseli puolittaa suoran
-akseli puolittaa suoran 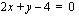 ja käyrän
ja käyrän 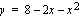 rajoittaman alueen pinta-alan.
rajoittaman alueen pinta-alan.
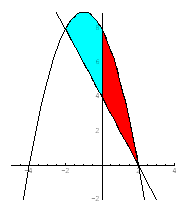
Lasketaan suoran 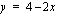 ja käyrän
ja käyrän 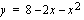 leikkauspisteet ratkaisemalla yhtälöparista muuttuja
leikkauspisteet ratkaisemalla yhtälöparista muuttuja 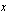 eli integroimiseen tarvittavat leikkauskohdat (integroimisrajat).
eli integroimiseen tarvittavat leikkauskohdat (integroimisrajat).
Sijoitetaan ylemmästä yhtälöstä 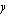 :n lauseke alempaan yhtälöön
:n lauseke alempaan yhtälöön 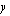 :n paikalle.
:n paikalle.
Integroimisvälillä käyrä kulkee suoran yläpuolella, joten pinta-alat saadaan integroimalla erotusfunktiota 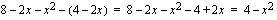 .
.
Jos 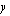 -akseli puolittaa kyseisen alueen, niin seuraavat alat
-akseli puolittaa kyseisen alueen, niin seuraavat alat 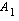 ja
ja 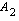 ovat yhtäsuuret.
ovat yhtäsuuret.
Pinta-alat ovat samat, joten 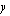 -akseli eli suora
-akseli eli suora 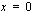 puolittaa suoran
puolittaa suoran 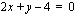 ja käyrän
ja käyrän 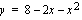 rajoittaman alueen pinta-alan.
rajoittaman alueen pinta-alan.
b ) Lasketaan sen äärellisen alueen ala, jonka rajoittavat suorat 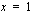 ,
, 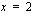 ja
ja 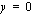 eli
eli 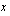 -akseli sekä käyrä
-akseli sekä käyrä
Tarkastellaan käyrän käyttäytymistä merkkikaavion avulla erityisesti integroimisrajojen sisällä, nimittäjän nollakohdan 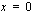 ja osoittajan nollakohdan
ja osoittajan nollakohdan 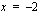 ympäristössä.
ympäristössä.
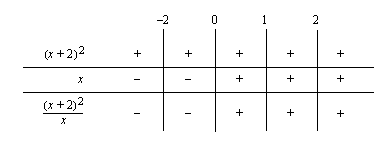
Integroimisvälillä käyrä kulkee 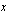 -akselin yläpuolella.
-akselin yläpuolella.
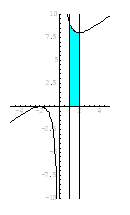
Pinta-ala saadaan integroimalla seuraavasti.
[Tehtävä 11.8][Vinkki tehtävään 11.8]