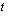Ratkaisu tehtävään 11.7

a ) Ratkaistaan millä 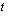:n arvolla

.

Poistetaan sulut ja lasketaan integraali termeittäin.

Määritetään sitten vakion 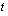arvo ratkaisemalla yhtälö tulon nollasäännön nojalla.

tai

Ensimmäinen ratkaisu 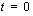on ilmeinen, jonka olisi voinut todeta jo aiemmin, sillä tyhjän välin integraali on aina nolla (Määrätyn integraalin geometrinen tulkinta). Toinen ratkaisu 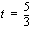on mielekkäämpi.

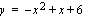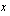b ) Lasketaan käyrän ja -akselin rajoittaman alueen pinta-ala. Käyrä on alaspäin aukeava paraabeli, joka saa positiivisia arvoja nollakohtiens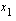a ja 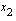välissä, ts. 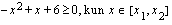. Ratkaistaan nollakohdat eli käyrän ja 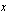-akselin leikkauskohdat ratkaisemalla yhtälö 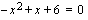toisen asteen yhtälön ratkaisukaavan avulla

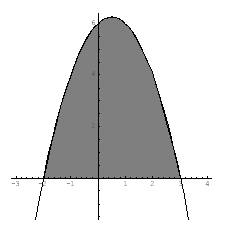
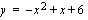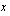Käyrän ja -akselin rajoittaman alueen pinta-ala saadaan integroimalla.

[Tehtävä 11.7][Vinkki tehtävään 11.7]

[Ylemmälle pääsivulle] [Edellinen sivu] [Seuraava sivu]